In what year do you think the first U.S. Social Security check was issued?
Two people are asked this question, neither knows the answer with certainty, so they separately are guided through a process to represent both their best guess and degree of uncertainty, resulting in the two probability distribution curves below, dating back to 1776. Which person did “better”?
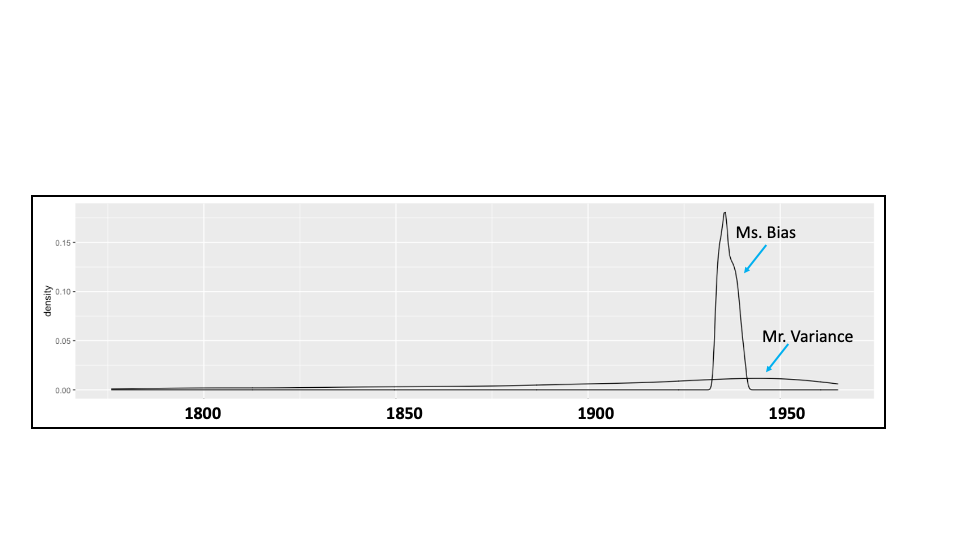
That depends on how we define “better”. Clearly, the flat-liner expressed much less confidence, but perhaps the confidence exhibited by the narrow-bander is misplaced. Let’s look at how each responded and performed.
Neither knew the answer off-hand, so they were asked to pick two extreme values, the minimal and maximal plausible values, and their single best guess, the 50th-percentile, such that in each of their respective views the correct answer was equally likely to be above or below that estimate. Next, each was asked to express their degree of uncertainty by specifying a 25th-percentile and 75th-percentile that properly reflects their uncertainty regarding this subjective distribution of possible answers. Surely each would agree that there is 100% likelihood the true answer is greater than 1 A.D., greater than 2 A.D., and so on — eventually reaching amounts believed highly implausible but nonetheless possible. Continuing on until reaching an amount such each believed there is about a 25% chance the true value is less than it and a 75% chance it is larger. That is Q1, a personal first quartile. Continue on until reaching Q2, a number representing an equal 50% chance the true value is lower or higher, and finally to Q3, signifying the personal view there is a 75% chance the number is lower and 25% chance it is higher. Notice that the respondent should be equally confident the true number is inside the range between Q1 and Q3 as that it is outside that range. That middle 50% of data is a subjective interquartile range (IQR). Overconfidence would be exhibited by a general tendency for subjective estimates of the IQR to exclude the true value more frequently than it includes it, so that the true value is lodged somewhere below Q1 or above Q3. For each person, we now have a five-poiont summary, the parameters of a distribution.
Ms. Bias
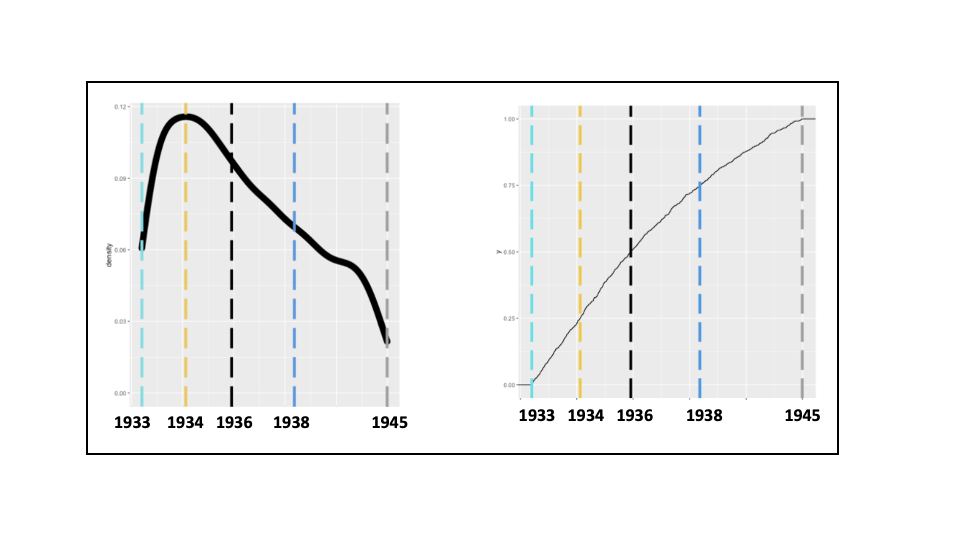
She recalls with assuredness that the Social Security program was a creation of Franklin Delano Roosevelt during his presidency, which she asserts as having run from 1933 to 1945. She believes the program likely started after his first year in office but before the Pearl Harbor bombing, and was equally likely to have occurred inside or outside a two-year window. Her five-number summary is:

The probability density function (pdf) and its cumulative values (cdf):
Mr. Variance
He confesses to having no idea. Pressed to offer something, he realizes that the answer must fall between 1776 and 2020, since it is a program of the United States government. That’s a start. Pressed further, he suggests the program likely was initiated following a significant historical event, lists five candidate events, and deems each event equally likely to have resulted in the initiation of Social Security. He maps out his thoughts, and decides those five dates correspond to the five-number summary that reflect his subjective beliefs:
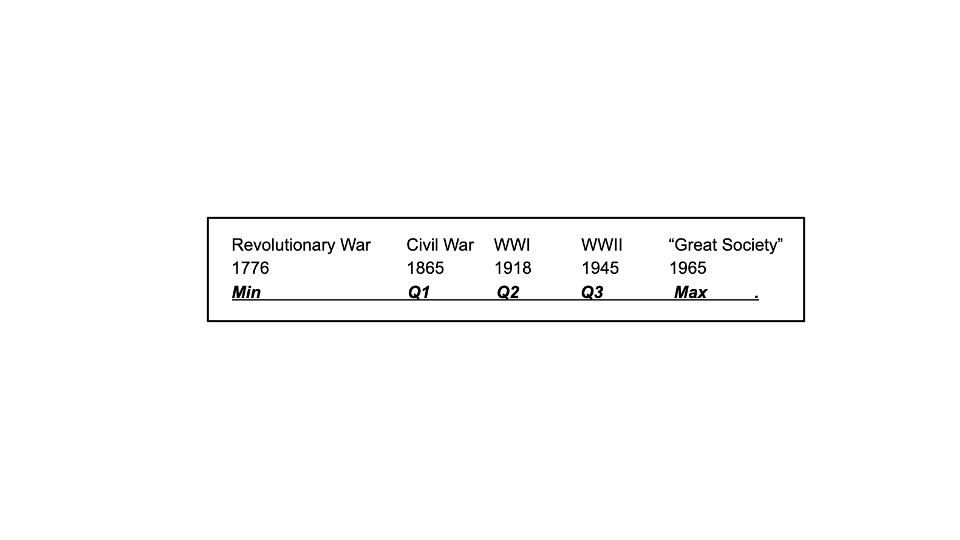
So, Mr. Variance believes the actual date is equally likely before or after 1918, with a 50% chance it happened between 1865 and 1945, and 25% probabilities each for the 1776-1865 or 1945-1965 intervals. Applying these parameters to the general lognormal distribution results in the following five-number summary, subjective probability density, and cumulative probability distribution. Note the initial estimates are slightly adjusted. That is because the five-number summary is a set of parameters, which are fed into a program to simulate distributions.
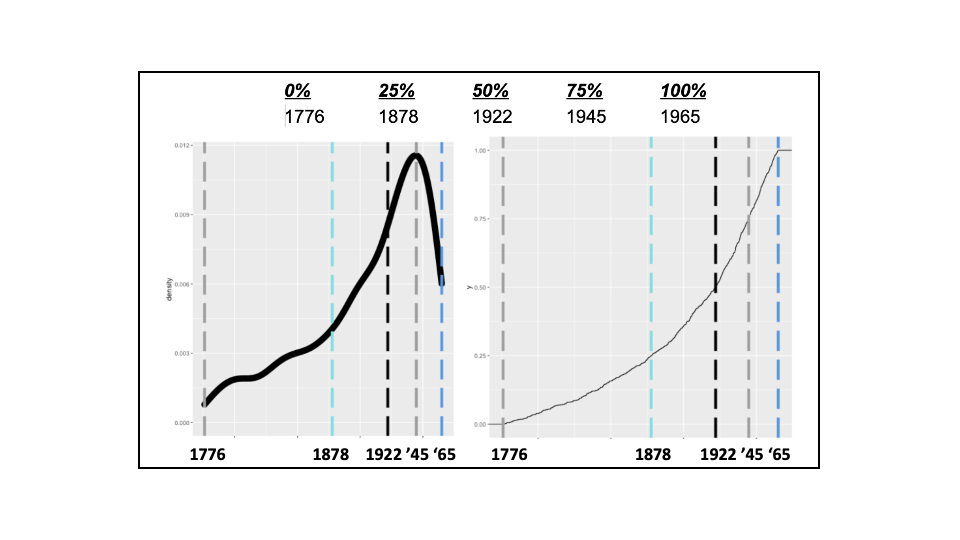
In fact, as part of his “New Deal”, it indeed was FDR who signed the Social Security Act of 1935. Although the first SSA office opened in 1936 and the first Social Security taxes were collected in 1937, the first check was not issued until January 31, 1940. The recipient of that first check was Ida May Fuller, a legal secretary who paid a total of $24.75 in Social Security taxes during 1937-38-39, then received that first check for $22.54 upon turning 65. In an ironic precursor of financial strains on the program, she lived to age 100, collecting $22,888.92 from SSA over 35 years.

Truly unbiased subjective curves would be centered at 1940, with equal belief the actual year would as likely be later than earlier than 1940. Based on their respective belief curves, for Mr. Variance 70.0% of the area under the simulated curve fell earlier than 1940, whereas 95.7% did so for Ms. Bias. Both are biased toward an earlier year, but Ms. Bias far more so.
Overconfidence is characterized by subjective confidence in judgements or beliefs that exceed the demonstrably objective accuracy of those judgements or beliefs. Psychology literature suggests it is far more common than being properly calibrated, and evidence of underconfidence is relatively sparse.
More Complex Example
Let’s work through a more complex example. You are asked to estimate the dollar value of all distributions of U.S. Social Security payments to beneficiaries during May, 2020. Assume you had responded Q1 = $1 billion, Q2 = $5 billion, and Q3 = $50 billion. I can conclude from this that your IQR does not include the true answer, but cannot from this conclude you are overconfident. After all, if you are properly calibrated, being inside/outside the IQR is a 50/50 proposition.
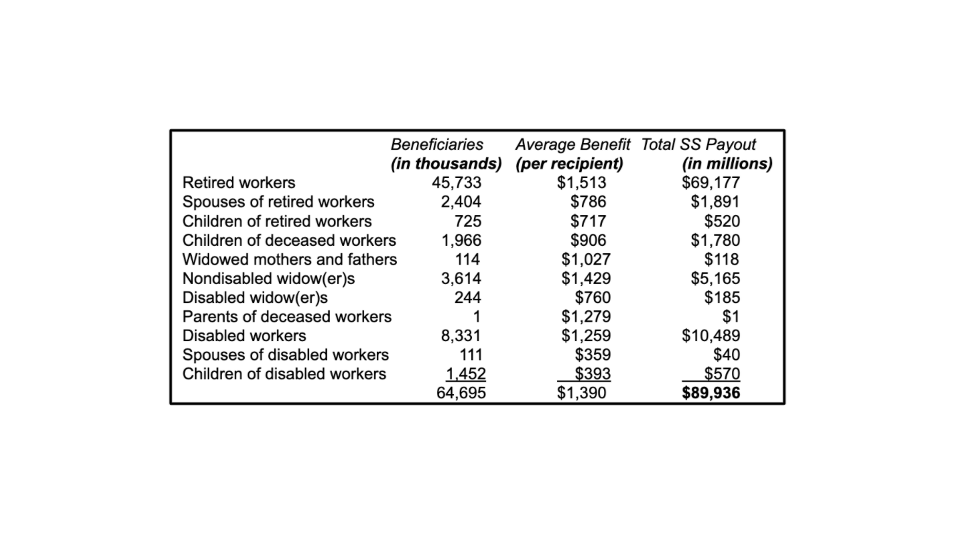
Given sufficient opportunity, time and access to resources, one could construct an informed estimate of the dollar value of all distributions of U.S. Social Security payments to beneficiaries during May, 2020. There are eleven types of recipients, and for each there is a record of the number of beneficiaries and the actual payout to each in May 2020. To multiply the number of beneficiaries times the average payout for each category of recipients requires 22 input values, and the sum of the 11 products equals a total payout by Social Security of about $90 billion ($89,939,234,989.04) during the month of May, 2020.
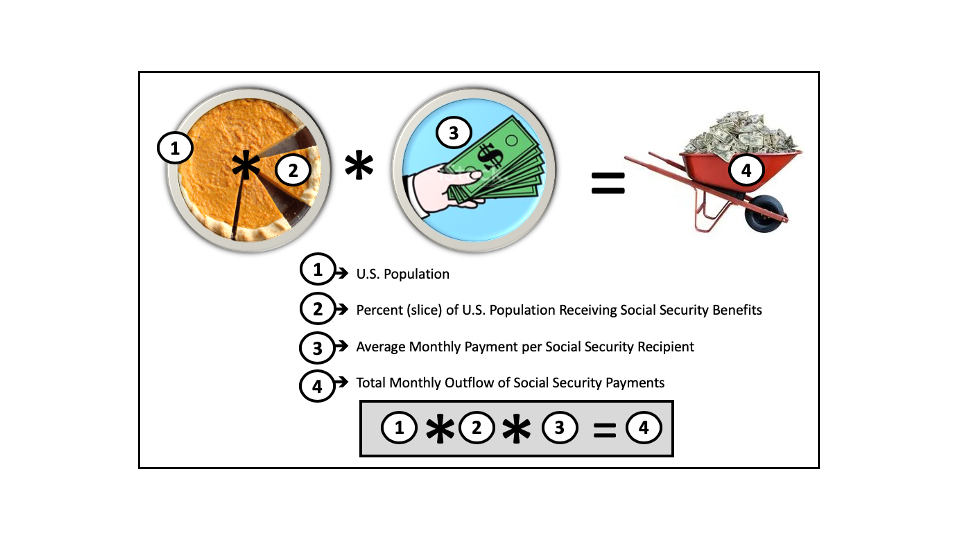
There is a compromise strategy, more elegant than the loosely-anchored initial estimates of Q1, Q2 and Q3, but far less computationally demanding than the explicit enumeration above. A “fast and frugal” compromise strategy is to provide subjective estimates for a small and manageable number of components that have the potential to reasonably substitute for a complete listing of categories, and that might more reasonably be estimated by an outsider than the required 22 input parameters above.
For example, one could device a four-parameter estimation process:
1. World population
2. U.S. population as percent of world
3. U.S. Social Security recipients as percent of population
4. Average monthly payment per Social Security recipient.
* Total Outflow of Social Security Benefits ~ Product of the four parameters.
If preferred, the problem can be simplified further, replacing the first two parameters by directly asking for the U.S. population, thereby reducing to a three-parameter estimation problem (but at a cost: loss of information):
1. U.S. population
2. U.S. Social Security recipients as percent of population
3. Average monthly payment per Social Security recipient.
* Total Outflow of Social Security Benefits ~ Product of three parameters.
Applying the latter three-parameter estimation process, you now are asked to provide Q1, Q2 and Q3 subjective estimates for each of the three parameters, as shown below. Taking the best guesses (Q2), your new estimate equals 15% of 320,000, times $4,000 per recipient, equalling $192 billion — quite a leap from your original estimate of $5 billion. Error rates for each component are as follow:
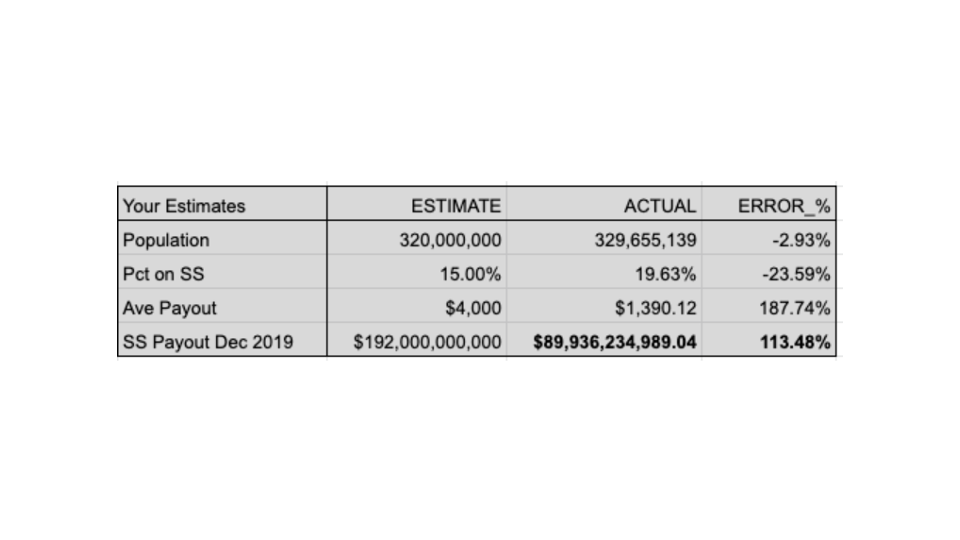
A single poor estimate greatly impaired your analysis, as your average payout per Social Security recipient is almost triple the actual value. With only three parameters to estimate, a single poor choice can greatly distort results. Nobody expects highly accurate estimates, but with more parameters to estimate, the opportunity for errors to offset and provide a decent final estimate increases greatly. For example, another person might complete the same three-parameter estimation process, with these results:
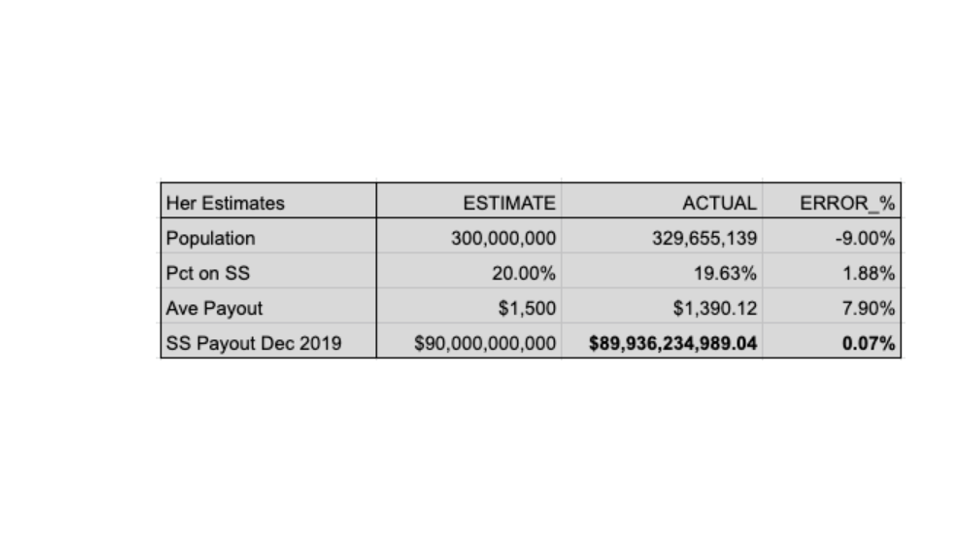
In her case, the two larger errors are in opposite directions, and essentially cancel their distortions. The three component estimates esch have much more error than the remarkably accurate final estimate, due to error cancellation.
Regarding the matter of assessment overconfidence, let’s return to your respective component quartile estimates and their implications. The table below displays your estimates (with actual correct answers in bold and to the far right):
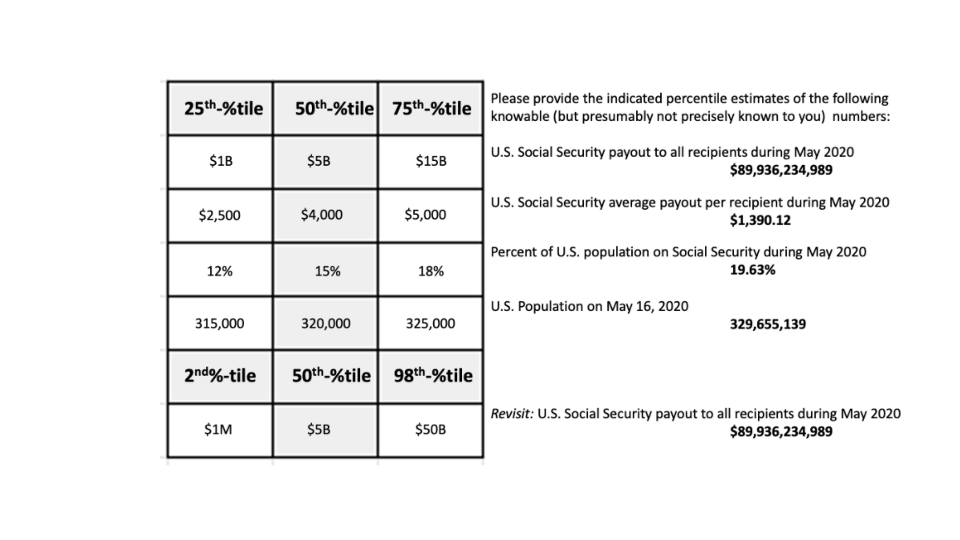
We now also have four independent estimates of Q1 and Q3 for independent questions, and note that the true values are outside the respective IQRs in all four cases, with three above Q3 and one below Q1. This provides preliminary evidence of overconfidence, although it must be noted that two estimates are relatively close to the Q3 bound and the sample size of n=4 can provide no more than tentative support for overconfidence, as opposed to a collection of several such three-parameter estimation processes.
Finally, note from the table above that you also were asked to provide estimates of the far tails to your original estimate of the dollar value of all distributions of U.S. Social Security payments to beneficiaries during May, 2020. In particular, while your best guess of the value was $5 billion, you also estimate your 2%-tile at $1 million, and your 98%-tile at $50 billion. Even this range does not capture the true value, as your 98th-percentile is little more than halfway to the actual value. This provides another indication of overconfidence. Also, your Q1 and Q3 estimates for the three-parameters imply a means of inferring your 2%-tile and 98%-tile beliefs regarding the total payout value. Since you believe there is only a 25% chance that a given true parameter value is below its Q1 estimate, and there are three parameters, you must believe there is a 25% * 25% * 25% (= 0.25^3 = 0.02, or 2%) chance that each of the three parameter values are below your respective Q1 estimates. The same applies to the other tail, at the 98%-tile. The visual display below provides an intuitive view of the calculations. Each quartile of a given parameter has an equal number of values, represented here by a 4×4 box with 16 cells per quantile. As we combine two parameters, we are left with 25% of the original cells below Q1 and above Q3, or four cells. Combining three parameters reduces cells by 25% again, from four down to one (1/16th of 16; 1/64th of the original 64 cells).
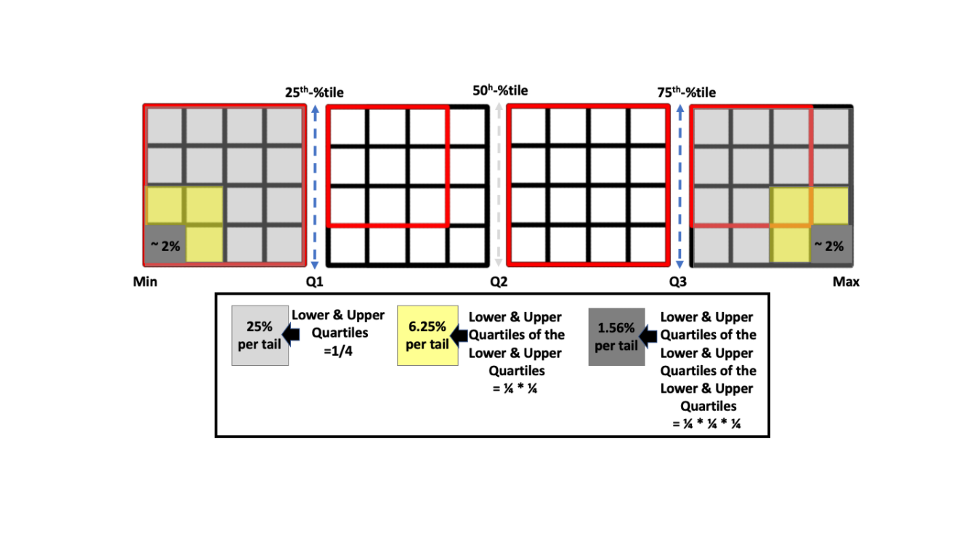
Applying this logic to your estimates, the implied percentiles are shown below. Your Q1, Q2 and Q3 estimates for each of the three parameter questions imply that your best guess estimate of the dollar value of all distributions of U.S. Social Security payments to beneficiaries during May, 2020 is $192 billion — quite the contrast to the direct estimate of $5 billion when initially asked. Further, the implication is that you believe there is about a 2% chance the true value exceeds $292.5 billion, and about a 2% chance it falls below $94.5 billion. Since the actual value is below that lower limit, there is evidence that you exhibit overconfidence in expressing subjective beliefs regarding objective values.
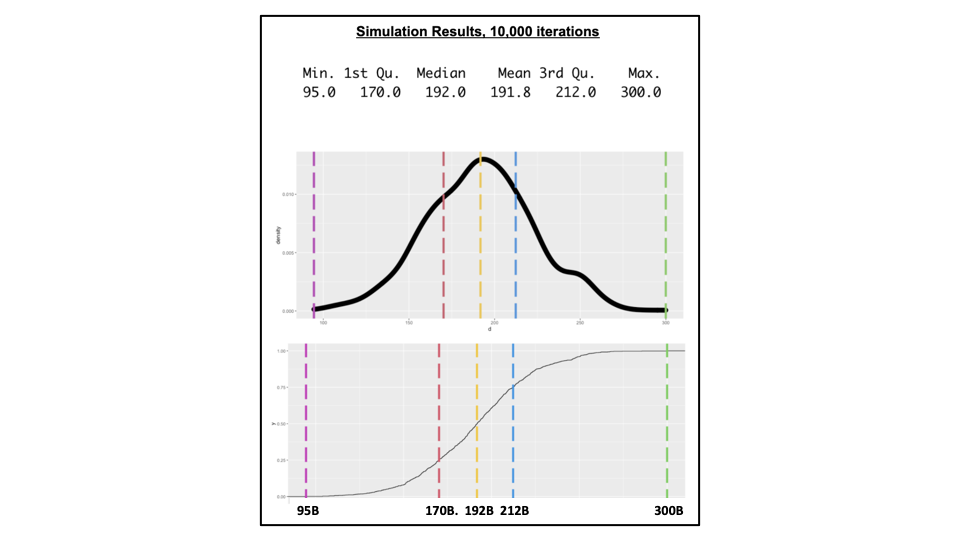
A Standalone APP
We have developed a standalone app to estimate the pdf and cdf of your subjective probability estimates to any problem by applying 10,000 iterations of a computer simulation of the general lognormal distribution, based on the five-number summary you enter.
— Jerry Platt, Ph.D., Emeritus Professor of Finance, San Francisco State U.
Comments 4,072
good content
instagram beğeni satın al, instagram türk beğeni satın al,
instagram ucuz beğeni gibi tüm işlemleri hemen sitemizden alabilir sizde paylaşımlarınızı renklendirebilirsiniz
Sosyal medya dünyasında instagram takipçi satın al işlemleri yapmak artık takipcisatinalin.org ile çok kolay !
hemen tıkla sende takipçi satın al
What’s Happening i am new to this, I stumbled upon this I’ve found It positively helpful and
it has helped me out loads. I am hoping to contribute & help different users like
its helped me. Great job.
Sosyalmedya hesaplarının arasında en hızlı gelişim instagram da gelişiyor..
İster bireysel ister kurumsal olarak instagramı doğru kullandığınızda sizlere çok büyük faydalar sağlanıyor instagram takipçi satın al
hizmeti için takip2018 web sayfasına giriş yapabilirsiniz.
Very good information. Lucky me I found your blog by chance (stumbleupon).
I have saved it for later!
Its not my first time to visit this site, i am visiting
this site dailly and take pleasant facts from here every day.
Have you ever thought about writing an ebook or guest authoring on other websites?
I have a blog centered on the same information you discuss and would really like to have you
share some stories/information. I know my subscribers
would enjoy your work. If you’re even remotely interested, feel free to send me
an email.
If some one desires to be updated with newest technologies therefore he must be
pay a visit this website and be up to date daily.
Birşey almadan önce herzaman araştırırız en güvenilir hangisidir diye.
en güvenilir takipçi satın alma sitesi de instagram da takip2018.com dur hemen en hızlı
takipçi al
I pay a quick visit everyday some blogs and sites to read content, but this website presents quality based articles.
Thanks for some other fantastic post. Where else may just anyone get that kind of info in such
an ideal manner of writing? I’ve a presentation next week, and I’m on the
search for such information.
Howdy! This article could not be written much better!
Reading through this post reminds me of my previous roommate!
He always kept preaching about this. I will send this
information to him. Fairly certain he’s going to have a
very good read. Thank you for sharing!
Amazing things here. I’m very happy to peer your post. Thanks a lot and I’m having a look
forward to contact you. Will you kindly drop me a mail?
İnstagram kullanıcıları daha aktif ve etkin olmasını istiyorsanız takipçi sayınızı belirli bir düzeye ulaştırmalısınız.
Bunun kendi imkanlarınızla kısa sürelerde
hallediyor olmanız neredeyse imkansızdır.
İnstagram takipçi satın al hizmeti ile hesaplarınızda istediğiniz sayılarda takipçi sahibi olabilirsiniz.
Bu alanda hizmet veren ve takipçi satışı yapan platformları kullanabilirsiniz takipcisatinalin.org
Instagram Takipçi Satın Al hizmetleriyle aktif bir
şekilde takipçi hizmeti veriyor
I delight in, lead to I found exactly what I was taking a look for.
You have ended my four day long hunt! God Bless
you man. Have a nice day. Bye
Hey! This post couldn’t be written any better! Reading through this post reminds me of my
good old room mate! He always kept chatting about this. I will forward this write-up to him.
Fairly certain he will have a good read. Thanks for sharing!
You can certainly see your skills within the work you write.
The sector hopes for even more passionate writers like you who are not afraid to mention how they believe.
All the time follow your heart.
It is in reality a nice and useful piece of info. I’m glad that you
shared this helpful info with us. Please keep us up to date like this.
Thank you for sharing.
I’m impressed, I have to admit. Rarely do I encounter a blog that’s both educative and amusing, and without
a doubt, you have hit the nail on the head. The issue is something which too few men and women are speaking intelligently about.
Now i’m very happy that I stumbled across this in my hunt for something concerning this.
Its like you read my thoughts! You appear to grasp so much approximately this, such as you wrote the ebook in it or something.
I believe that you just could do with a few percent to power the message
house a little bit, however other than that, this is excellent blog.
A fantastic read. I will certainly be back.
Saved as a favorite, I like your site!
Hi there I am so happy I found your website, I really found you by accident, while I
was searching on Yahoo for something else, Nonetheless
I am here now and would just like to say many thanks for a tremendous post
and a all round thrilling blog (I also love the
theme/design), I don’t have time to look over it all at the minute but I have saved it
and also added your RSS feeds, so when I have time I
will be back to read a great deal more, Please do keep
up the excellent job.
Hello to every single one, it’s truly a good for me to visit this site,
it consists of priceless Information.
This excellent website certainly has all the information I needed about this subject and didn’t know who to ask.
When I initially left a comment I seem to have clicked the -Notify me when new comments are added- checkbox and from now on whenever
a comment is added I get four emails with the same comment.
There has to be a way you are able to remove me from that service?
Many thanks!
Hello I am so thrilled I found your site, I really found you by mistake, while I was researching on Yahoo for something else, Anyhow I am here now and would just like to say
cheers for a tremendous post and a all round exciting
blog (I also love the theme/design), I don’t have time to look
over it all at the minute but I have saved it and also included your RSS feeds,
so when I have time I will be back to read a great deal more, Please do keep up the fantastic job.
aşam alanlarımızda sık sık rastladığımız hamam böceği problemleri,
kısa vakit içinde araya girmek edilmez ise çok daha değişik boyutlarda sorunlara niçin olabilirler.
antalya böcek ilaçlama Hamam böcekleri dolaştıkları her
ortamdan bünyelerine detaylı bakteri taşımaktadır.
Daha sonra bu bakterileri de girmiş oldukları her alanda yayarak, başka
canlı türlerinin sağlığını rizikoya atabilmektedir.
Bu amaçla hamam böceği ilaçlama faaliyetlerinin önemi gerektiğince büyüktür.
Greetings, There’s no doubt that your web site could be having web
browser compatibility problems. When I take a look at your web site in Safari, it
looks fine however when opening in Internet Explorer,
it’s got some overlapping issues. I just wanted to provide you with a quick heads
up! Apart from that, fantastic blog!
instagram gerçek türk beğeni satın al denilince akla hemen ilk gelen site
olan sitemiz hemen size yılların verdiği
tecrübe ile sizlere hala kesintisiz hizmet
vermekte. Türk ve gerçek beğeni satın alabilmek için tercih sebebi
olan bu siteden hemen faydalanabilirsiniz, Bu sayede profiliniz herkes tarafından sevilecek ve heryerde sizden bahsedecekler.
Türk beğeni almanın faydalarından biri faydası ise gönderileriniz keşfete düşer.
Aynı zamanda türk oto beğeni sağlayıcısıdır.
Oto beğeni siz paylaşım yaptığınız an belirttiğiniz sürede
paylaşımınız ister foto ister video ne olursa olsun otomatik olarak size ulaştırılır.
Shell indirme test sitesi
site de belirtmiş olduğumuz gibi herşeyin sana
özgün olarak logsuz olmalı logsuz shell indir adresi shelldownload.org
Instagram Takipçi Sayısının Önemi
Günümüzde neredeyse en çok kullanımının olduğu
uygulama olan instagram uygulamasında kullanıcılar kendilerini
daha yaygın ve daha yüksek etkileşimler almanın etkisine kaptırmış durumdadır.
Bu nedenle kişiler daha fazla etkileşim alabilmek adına
ve daha yaygın bir kitleye ulaşabilme imkanı elde etmek isterler.
Bu kişilerin takipçi satın al gibi
platformlar aracılığı ile gerçek takipçiye sahip olarak etkileşimleri en kısa zamanda en yüksek seviyelere taşıma imkanı elde ederler.
I was wondering if you ever considered changing the page layout of your website?
Its very well written; I love what youve got to say.
But maybe you could a little more in the way of content so people could connect with it better.
Youve got an awful lot of text for only having 1 or two pictures.
Maybe you could space it out better?
antalya böcek ilaçlama Şirketi olan alc
ilaçlama ile tüm haşarelerden korunmaya hazırmısın?
Böcek ilaçlama lider firması olan titiz ve hızlı personeli sayesinde belirttiğiniz saatte hemen hizmet
vermektedir.
Priv8 shell için Shell Download sitesine giderek hemen shell
d
wso shell indirererk sunucunu hemen test et
wso shell download için shelldownload.org ziyaret edin
Logsuz shell download için hemen siteyi ziyaret et sende shelller ile serverlarını test et
En iyi takipçi satın al sitesini kullanarak popülerliğini arttırma
Takipçi satın al!
It is appropriate time to make some plans for the future and it’s time to be happy.
I have learn this submit and if I could I wish to counsel you few fascinating issues or suggestions.
Perhaps you could write subsequent articles relating to this article.
I wish to learn more issues approximately it!
Takip2018.com ile takipci satin al
Sitemizin yer alan paketler bunlarla sınırlı değil.
Sitemizde görünenlerle sınırlı değildir, dilediğiniz kadar instagram takipci satin al seçeneklerinden dilediğiniz kadar alabilirsiniz.
Ucuz Takipçi Alarak Fenomen Olabilirsin
Instagram da artık basit bir halde fenomen olabilirsiniz.
Takipçilerinizi hızlı ve etken bir şekilde arttırmak istiyor musunuz?
hemen bu siteye giriş yaparak tüm takipçi hizmetlerinden hızlı bir şekilde faydalanabilirsiniz.
Sizlere en kaliteli takipçi sistemlerini sunarak, kısa vakit arasında istediğiniz kadar
takipçi gönderimi yapıyor. Sitede yer alan ucuz takipçi satın al hizmetinden faydalanarak arzu ettiğiniz kadar takipçiye ulaşabilirsiniz.
Bu site sizden aslabir şekilde hesap şifresi istemiyor.
sadece kullanıcı isminiz ehil oluyor. uzun zamandır bu mevzuda hizmet veren bir site olarak, sizlere en kaliteli ve güvenilir takipçi hizmetlerini
sunuyor. Siteye tek tıkla giriş yaparak arzu ettiğiniz kadar takipçiyi hesabınıza gönderebilirsiniz.
Tamamen rahat yöntemlerle dilediğiniz kadar takipçiye ulaşabiliyorsunuz.
Thanks a bunch for sharing this with all folks you really realize what you’re speaking approximately!
Bookmarked. Kindly also talk over with my website =).
We will have a hyperlink alternate contract among
us
Incredible story there. What occurred after? Thanks!
When I initially commented I seem to have clicked on the -Notify me when new comments are added- checkbox and from now on each time a comment is
added I get four emails with the exact same comment.
Is there a means you can remove me from that service?
Appreciate it!
Aktif gerçek İnstagram Takipçi Satın AL işlemini gerçekleştir!
instagramaktiftakipci ile en hızlı takipçi satın al
Instagram aktif takipçi satın alarak siz de fenomen olabilirsiniz, fakat fenomen olmak isterken aynı zaman da bu
işlemleri yapacağınız yerin kalitesi çok önemlidir bunu unutmayınız.
Türk takipçi yazarak yabancı takipçi atılırsa hesabınıza bu sizin hesabınızın gerek
görüntü gerek keşfete düşme gibi olasılıklarınızı tamamen bitirecektir.
Bu yüzden aktif takipçi almanız çok önemli, aynı zamanda tabiki güvenilirlik ön planda olmalıdır.
Biz uzman ekibimiz ile sizlere en iyi hizmeti vermek için sürekli çalışmaktayız.
En iyi takipçi beğeni izlenme gibi sizleri üst seviyeye çıkarmak için elimizden geleni yaptık ve
yapmaya devam edeceğiz. Ucuz Instagram takipçi için bizimle de iletişime geçebilirsiniz.
Instagram bot takipçi içinde geçebilirsiniz fakat bunlara garanti
vermemekteyiz, bot takipçilerin kesinlikle garantisi yoktur bir kaç gün içerisinde hepsi Instagram tarafından silinebilir.
En aktif siteden hemen sende instagram aktif takipçi satın al
Heya i am for the first time here. I found this board and I find It truly useful &
it helped me out much. I hope to give something back and aid others like you aided me.
Instagram takipci sayfanızın satış için yada popülerliğinizi arttırmak için takipci satin al islemini gercekleştirin
Instagram takipçi hizmetlerinden yararlanabilmek amacıyla ilk olarak istenilen hizmetin tercihinin yapılması gerekmektedir.
Sonra ise shopier ekranında sadece kullanıcı adınız ve 3d ödeme yöntemi ile ödeme yapmanız gerekmektedir.
Burada doğru bulguların girildiğinden emin olunması, hizmet yönünden problem yaşamamak
amacıyla önemlidir.
Her yaştaki isteyen herkes Takipçi satın al işlemi takip2018 den yapabilirler.
I’m impressed, I must say. Seldom do I come across a blog that’s both educative and amusing, and
without a doubt, you have hit the nail on the head.
The issue is something which too few folks are speaking intelligently about.
I’m very happy that I came across this in my hunt for something concerning
this.
Thanks for any other informative site. The
place else may just I get that type of info written in such an ideal approach?
I have a project that I’m just now running on, and I’ve been on the glance out for such information.
Şirketi olan alc ilaçlama ile tüm haşarelerden korunmaya hazırmısın?
Böcek ilaçlama lider firması olan titiz ve hızlı personeli
sayesinde
belirttiğiniz saatte hemen hizmet vermektedir antalya böcek ilaçlama
Lider firma bir telefon kadar yakın!
Instagram hesabını büyüterek onbinlerce seni takip eden olsun istiyorsan instagram takipçi al websitesinden hemen faydalan!
Instagram da artık basit bir halde fenomen olabilirsiniz.
Takipçilerinizi hızlı ve etken bir şekilde arttırmak istiyor musunuz?
hemen bu siteye giriş yaparak tüm takipçi hizmetlerinden hızlı bir
şekilde faydalanabilirsiniz. Sizlere en kaliteli takipçi sistemlerini sunarak, kısa vakit arasında istediğiniz kadar takipçi
gönderimi yapıyor. Sitede yer alan İnstagram takipçi Satın Al hizmetinden faydalanarak arzu ettiğiniz kadar takipçiye ulaşabilirsiniz.
I pay a visit day-to-day a few blogs and information sites to read articles, however this
weblog gives feature based articles.
Türk gerçek ve yabancı gerçek gibi 50k 100k 1m gibi Takipçi Satın Al
seçenekleri ile takipçilerini hemen toparla!
Instagram için eşsiz benzersiz hizmetler sunan takip2018 den instagram takipçi al 1000, 2000 gibi bir çok seçenek ile
instagram takipçi satın al
Instagram hesabınızı büyütmek ve yeni müşteriler
yada arkadaşlara
sahip olmak için çok fazla düşünmenize kesinlikle gerek yoktur.
Geri takipler ile uğraşmak yerine hemen takip2018.com a giderek
Takipci Satin Al
işleminizi kolayca halledebilirsiniz
Fenomen ve populer bir kişi olmak için hemen siteyi ziyaret et
Sivilce ve her türlü cilt tonu lekeleri için hc Leke Kremi
ile cilt rengi farklılıklarına son !
Bizler antalya firması olarak çalışmalarımıza yön veren izolasyon uygulamaları
ile siz müşterilerimize en iyi izolasyon uygulamaları yapabilmek adına en kaliteli çatı izolasyon ustaları, ile sizlere hizmet vermekteyiz.
Çatıcı, olarak günümüzde yapmış olduğumuz yalıtım uygulamaları
sayesinde müşteri memnuniyetini kazanmış ve kalitesinden asla ödün vermemiş Babadağ çatı, asla
düzenini bozmadan izolasyon uygulamasına devam etmektedir.
antalya izolasyon
En aktif ve türk gerçek Takipçi Satın Al sitesi olan sitemizden hemen en aktif takipçileri satın al
Instagram’da bir hesabın takipçi sayısı, o hesabın prestiji açısından çok önemlidir.
Bundan dolayı, hesabını büyütmek isteyenler,
öncelikle takipçi satın almaktadır. Fazla takipçi sayısı olan hesaplar,
daha fazla dikkat çeker ve daha fazla kişiye ulaşırlar.
Firma, müşterilerin farklı taleplerine cevap verebilmek
adına farklı takipçi paketleriyle hizmet vermektedir.
kaliteli takipçi satın al
kelimesinde en iyi web sitesi!
.
Hc care leke kremi
HC Pigment-Control’ün cilt lekelerine karşı hızlı ve güçlü etkisi,
Kuzey Kanada Bozkırları’na özgü bir tarla bitkisi olan Rumeks’ten (Tyrostat™), tabiatın yeniden canlandırma mucizesi olan Yeniden Diriliş Bitkisi’ne kadar birçok
doğal ve saf aktif bileşene dayalıdır.
Tüm bu aktif bileşenlerin, lekeler ve cilt yaşlanması üzerindeki etkileri in-vivo testler ve klinik
laboratuvar çalışmalarıyla kanıtlanmıştır.
Tüm cilt tiplerinde, leke problemlerini giderme ve önlemede, cilt tonu eşitsizliğinde, cilt aydınlatmasında, nem
ihtiyacı olan ciltlerde güvenle kullanılabilir.
En iyi leke kremi
Sosyal Medya platformlarının tamamı içn takipçi satın al hizmeti sunmaktayız
https://rebrand.ly/takipci-satin-al-
Üstelik dilediğiniz kadar takipçi yada beğeni alabilirsiniz bu eşsiz hizmetten hemen faydalanmak seninin de hakkın gülo
Instagram’da bir hesabın takipçi sayısı, o hesabın prestiji açısından çok önemlidir.
İnstagram kullanıcılarının sayısı her geçen gün artıyor.
İnstagram da fenomen olmak isteyen kişiler ise bir birleri ile yarışıyor
https://rebrand.ly/instagram-takipci-satin-al-
Takipcisatinalin.org ile hemen instagram takipçi satın al.
Tr Medya sitesi aracılığı ile istediğiniz sayılarda instagram takipçisi satın alabilirsiniz.
Bu satın alma işlemini yaparken hazırlanmış olan takipçi paketlerinden istediğinizi seçebilirsiniz.
Her zaman en uygun fiyatların sunulduğu takipçi paketlerinden her biri her bütçeye uygun olarak hazırlanıyor.
Bütçenize ve ihtiyacınıza en uygun olan paketleri seçebilirsiniz.
https://rebrand.ly/takipci-satin-al
Please let me know if you’re looking for a article author
for your site. You have some really great articles and I believe I would be a good asset.
If you ever want to take some of the load off, I’d love
to write some material for your blog in exchange for
a link back to mine. Please send me an email if interested.
Cheers!
Piece of writing writing is also a fun, if you be acquainted with
then you can write or else it is complex to write.
I’m gone to inform my little brother, that he
should also go to see this web site on regular basis to get updated from hottest
information.
I know this if off topic but I’m looking into starting my
own weblog and was curious what all is needed to get setup?
I’m assuming having a blog like yours would cost a pretty penny?
I’m not very web smart so I’m not 100% positive.
Any tips or advice would be greatly appreciated.
Thank you
Türkiyenin en iyi markası olan hc care artık sizlere leke kremi ile de içten karşılamtakta.
Tamamen doğal ürünlerden üretilen bu en iyi leke kremini kullanmadan cildinize küsmeyin !
https://bit.ly/eniyilekekremi-
Türkiye nin lider sitesi instagramaktiftakipci.com ile Instagram için geçerli türk takipçiler almaya hazırmısın?
Ucuz fiyatlara kalitenin en iyi adresi ile tanışmak sadece bir tık kadar
yakın.. http://bit.ly/turk-takipci-satin-alma
Hemen instagramaktiftakipci den aktif türk takipçiler
alın
Instagram ve diğer soysal medyalar için gerek takipçi gerek beğeni gibi bir çok sizi populeriter gösterecek tüm ürünlere hemen ulaşmak için kısacası takipçi almak için Hemen tıkla ve satın al
https://bit.ly/instagram-takipçi-satın-alma
Do you have any video of that? I’d care to find
out some additional information.
En güvenilir takipçi sitesi ile profiliniz için Takipçi Satın AL işlemi hemen en hızlı şekilde profilinize yüklenir.
Great post. I was checking continuously this blog and I am impressed!
Very useful info specifically the last part 🙂 I care for such info a lot.
I was looking for this certain information for a long time.
Thank you and good luck.
You should be a part of a contest for one of the finest blogs on the web.
I’m going to recommend this website!
Superb site you have here but I was curious about if you
knew of any user discussion forums that cover the same topics talked about in this article?
I’d really like to be a part of online community where I can get feedback from other experienced individuals that share the
same interest. If you have any suggestions, please let me know.
Kudos!
It’s difficult to find well-informed people for this subject, but you seem like you know
what you’re talking about! Thanks
I think everything published was very reasonable. However, think on this, suppose you were to create a awesome headline?
I mean, I don’t wish to tell you how to run your blog,
however what if you added something to maybe get
people’s attention? I mean Quantifying Your Subjective Beliefs | RetirementFinance.Org is a little
boring. You ought to look at Yahoo’s home page and watch how they write post headlines to grab
viewers to open the links. You might add a video or a related picture or two
to grab people interested about what you’ve got
to say. In my opinion, it would make your website a little livelier.
I like it when folks come together and share opinions. Great
blog, stick with it!
Amazing blog! Do you have any hints for aspiring writers?
I’m hoping to start my own blog soon but I’m a
little lost on everything. Would you recommend starting with a free platform like WordPress
or go for a paid option? There are so many options out there that I’m totally overwhelmed ..
Any suggestions? Many thanks!
Hmm it appears like your blog ate my first comment (it was extremely long) so I guess I’ll just sum it up what I wrote and say, I’m thoroughly enjoying your blog.
I too am an aspiring blog blogger but I’m still new to everything.
Do you have any helpful hints for inexperienced blog writers?
I’d definitely appreciate it.
Somebody necessarily help to make significantly articles I would
state. This is the very first time I frequented your web page and so far?
I surprised with the research you made to make this particular
publish incredible. Wonderful activity!
Link exchange is nothing else but it is just placing the other person’s blog link on your page at appropriate place
and other person will also do similar in support of you.
Sweet blog! I found it while surfing around on Yahoo News.
Do you have any tips on how to get listed in Yahoo News?
I’ve been trying for a while but I never seem to get there!
Many thanks
Hi there would you mind sharing which blog platform you’re using?
I’m looking to start my own blog in the near future but
I’m having a hard time deciding between BlogEngine/Wordpress/B2evolution and Drupal.
The reason I ask is because your design seems different then most blogs and I’m looking for something
unique. P.S Apologies for getting off-topic
but I had to ask!
Pretty part of content. I just stumbled upon your blog
and in accession capital to assert that I get in fact loved account your blog
posts. Any way I will be subscribing for your augment or even I achievement you get admission to persistently rapidly.
Thank you for the auspicious writeup. It in truth was once a leisure account it.
Glance advanced to far added agreeable from you! By the way, how could we be in contact?
Wow, awesome blog layout! How lengthy have you been blogging for?
you make running a blog glance easy. The overall look of
your site is great, let alone the content material!
Quality articles or reviews is the crucial to invite the people to visit the web site, that’s what
this web page is providing.
Just wish to say your article is as astounding.
The clearness in your post is simply nice and i can assume you are an expert
on this subject. Fine with your permission let me to grab your RSS feed to keep up to date with forthcoming post.
Thanks a million and please carry on the enjoyable work.
Hello friends, its wonderful piece of writing concerning tutoringand fully defined, keep it up all
the time.
When someone writes an article he/she keeps the plan of a
user in his/her brain that how a user can know it. So that’s why this paragraph is great.
Thanks!
This is really interesting, You’re an overly professional
blogger. I’ve joined your rss feed and look ahead to searching for extra of your wonderful post.
Also, I’ve shared your site in my social networks
Hi there! This post could not be written any better!
Looking at this article reminds me of my previous roommate!
He continually kept talking about this. I am going to forward this post to him.
Fairly certain he’s going to have a very good read. Many thanks for sharing!
Hi there! This is my first visit to your blog!
We are a team of volunteers and starting a new project in a community in the same niche.
Your blog provided us beneficial information to work on. You have done a extraordinary job!
I do not even know how I ended up right here, however I believed this publish was great.
I don’t understand who you might be however certainly you are going to a well-known blogger for those who aren’t already.
Cheers!
Thank you for some other informative web site.
Where else may I am getting that type of info written in such a
perfect manner? I have a undertaking that I’m just now operating on, and I’ve been on the
look out for such info.
Hi! Do you know if they make any plugins to safeguard
against hackers? I’m kinda paranoid about losing everything
I’ve worked hard on. Any recommendations?
Excellent blog you have got here.. It’s difficult to find
high-quality writing like yours these days. I really
appreciate individuals like you! Take care!!
Türkiyenin önde gelen cilt ürünleri firmasından hccare artık
sizlere leke kremi ile de hizmet vermekten gurur duyuyor,
En iyi leke kremini alabilmek artık çok kolay web sitesine giderek hemen leke kremi sahibi
olabilirsini
En iyi leke kremi ; https://cutt.ly/en-iyi-leke-kremi
Hey! Would you mind if I share your blog with my twitter group?
There’s a lot of people that I think would
really appreciate your content. Please let me know. Many thanks
When I originally commented I clicked the “Notify me when new comments are added”
checkbox and now each time a comment is added I get several emails
with the same comment. Is there any way you can remove me from that service?
Cheers!
What i do not realize is in truth how you’re
no longer actually much more well-preferred than you might be now.
You’re so intelligent. You recognize therefore significantly when it
comes to this subject, made me personally imagine it from
a lot of numerous angles. Its like men and women don’t seem to be
fascinated unless it’s one thing to do with Girl gaga! Your individual stuffs outstanding.
All the time deal with it up!
Hi there, of course this article is really fastidious and I have learned lot
of things from it regarding blogging. thanks.
Terrific post however I was wanting to know if you could write a litte more on this topic?
I’d be very grateful if you could elaborate a
little bit further. Thanks!
Türkiye de herkes youtube abone satın almak için takip2018.com u tercih ediyor,
Youtube abone seçenekleri türk ve yabancı paketler bulunmaktadır.
Hemen sizleride sitemize bekliyoruz
Ayrıca paketleri inceleyerek düşmeyen takipçi satın alma seçenekleride bulabilirsiniz,
Hatta ve hatta 8 tl ye bile instagram takipçi satın alabilirsinizz
Youtube Abone Satın aL‘ U Herkes tercih ediyor!
Hey there! I just wish to offer you a huge thumbs up
for the great information you’ve got right here on this post.
I will be returning to your blog for more soon.
Magnificent site. Plenty of useful information here.
I’m sending it to a few friends ans additionally sharing
in delicious. And naturally, thank you in your
sweat!
Instagram takipçi satın alarak profilini büyüt, satışlarını yükselterek en iyi takipçi paketlerine sahip olan siteyi
kesinlikle sana tavsiye diyoruz.
Takipçi satın alma konusunda uzman kadrosu ile sizi bekleyen bu site ile ucuz ve garantili gerçek türk kişilere
ulaşabilirsin. HEmen instagram takipçi satın al
https://rebrand.ly/takipcintr
Today, I went to the beach front with my kids.
I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.”
She placed the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is totally off topic but I had to tell someone!
payday cash
money advance
auto loans
no credit check payday loans
top payday loans
payday loans direct lender
can you buy viagra in australia
loans online no credit check
brand viagra online
mexican pharmacy
cash loans
SAÇ DÖKÜLMESİNE KARŞI GÜÇLÜ VE ETKİN BAKIM
Saç dökülmesi ile mücadele bazen zorlu bir maratona dönüşebilir.
Bu maratona HC Doping ile bir adım önde başlayın…
Bitiş çizgisine geldiğinizde saçlarınızdaki değişimi ve
ne kadar güçlendiğini hissedeceksiniz…
Üstelik hergün sadece 2 dakikanızı ayırarak.
HC Doping’in procapil, follicusan, bitki özleri ve vitaminler içeren formülü,
saçlarına ihtiyaç duyduğu desteği kazandırmak isteyen her
yaş aralığındaki kadın ve erkek için uygundur.
HC Doping’in formülünde, saçlarınızın ihtiyacı olan doğadaki yararlı bileşenler mevcuttur.
Ayrıca bir başka ürün kullanmanızı gerektirmeyecek
ölçüde zengin içeriği, saçınız için uygun oranlarda formülize edilmiştir.
Birçok saç bakım ürünün aksine HC Doping oldukça kolay bir kullanıma sahiptir.
Saçta kalıntı veya kötü koku bırakmaz. Uyguladıktan sonra durulamaya veya yıkamaya gerek yoktur.
Saç Bakım
installment loan companies
viagra price in india online
personal loan interest rates
loan identifier
cash advance loans online
loans fast cash
tretinoin 0.5 cream buy online
secured loan
loans bad credit
cash in one hour
[url=https://instcashadvance.com/]direct lenders of loans[/url]
payday loan online
how to get quick money
personal loans for people with bad credit
loan apply
sildenafil pharmacy online
no faxing payday loan
2000 loans
viagra super active plus
It is actually a nice and helpful piece of info. I’m satisfied that you shared this helpful
info with us. Please stay us informed like this. Thanks for sharing.
best online loans
bad credit loan
low income payday loans
va home loans
best viagra online australia
loans for poor credit
propecia tablets for sale
sildenafil soft tabs
loans without credit check
online payday cash advance
clomid pills
sildenafil citrate 100mg tab
tretinoin cream 0.05
tadalafil 20 mg buy online
where to buy fildena 100
generic viagra medication
loans guaranteed approval online
buying viagra in australia over the counter
global pharmacy
tadalafil cost in india
HC Vitamin-C Serum, özel olarak geliştirilmiş yüksek stabilite özelliğine
sahip Lipozomal Vitamin-C kompleksi ve en ileri düzeyde konsantre
edilmiş saf Hyaluronik Asit ile formülize edilen yoğun bakım serumudur.
Liposomal C Vitamini Serumu , Saf Hyalüronik Asit, Yeniden Diriliş Bitkisi (Glyceryl
Glucoside), Pentavitin (Saccharide Isomerate) ve Anadenanthera Colubrina Bark
Extract içeren formülü ile ciltte oluşabilecek lekeleri
minimuma indirmeye ve kırışıklıkları önlemeye yardımcı olur.
Çevresel faktörlere karşı etkili korumayı destekler.
Yoğun nemlendirici ve tazeleyici özelliği sayesinde cildin sıkılığını arttırır ve aydınlanmasını destekler.
Ciltteki ton eşitsizliklerine karşı mücadele eder.
Kozmetik piyasasında bulunan C vitamini serumu bir çoğunda Askorbik Asit’in stabil
olmayan %15’lük formu kullanılmaktadır. Bu ürünler stabil olmadıklarından zamanla okside olur, rengi koyulaşır ve doğal olarak da
zamanla etkinliğini kaybeder.
HC Vitamin-C Serum içerisinde stabil formda ve lipozomal kapsül şeklinde %3′ lük Etil Askorbik Asit kullanılmıştır.
Lipozomal taşıyıcı sistemler, hedef noktaya aktif maddeyi taşımak için geliştirilen üst düzey teknolojidir.
Ürün içindeki aktif madde (C VİTAMİNİ) cilt altına indikten sonra çözülür ve daha kısa sürede maksimum etki gösterir.
Bu sayede hem uzun raf ömrü boyunca stabilitesini kaybetmeden etkisini sürdürür,
hem de etkisi diğer formlara göre çok daha başarılıdır.
c vitamini serumu
canadian pharmacy viagra 150 mg
levitra 20mg coupon
stromectol tablets
loan for bad credit
no teletrack payday loans
how to buy genuine viagra online
cash payday loans
cialis australia prices
bad credit catalogues
generic cialis 10
san antonio payday loans
purchase cialis online from canada
personal loans unsecured
cash loans
generic cialis 40mg
tadalafil cheap online
40 mg tadalafil
starter loan
emergency loans
tadalafil generic mexico
hydroxychloroquine sulfate tablet
loans instant approval
small loan no credit
online loans
sildenafil 50mg price australia
secured loan
diflucan 200 mg
cialis 4 sale
stromectol tab price
İnstagram Takipçi Satın Alınabilir Kaliteli Site!
İnstagram hesaplarınızın aktif ve yükselen bir takipçi grubuna haiz olması için son yıllarda takipçi satın alma işlemi yapılıyor.
Bu işlem sayesinde takipçi rakamlarınızın artması olası oluyor.
Hesabınızın tercih edilme olasılığını arttırmak için instagram takipçi satın almak en kolay yol
olduğunu hepimiz biliyoruz.
aktif bir hesap sahibi olmak için bu kolay seçeneklerden yararlanabilirsiniz.
Hesaplarınızla ses getirmek istiyor ve size özel bir hesap özelliği kazandırmak
için instagram takipçi satın almak ve beğeni sayılarına da özen işaret etmek örutubet taşır.
Takipçi satın alma ve gönderme hizmetleri arasında şifresiz takipçi alma işlemi de bulunuyor.
İnstagram takipçi satma sayfaları genellikle otomasyon sistemine dayalı bir halde çalışır.
Tek yapmanız gereken sitemize giderek size uygun paketi seçmek olacaktır…
Başlatmış olduğunuzda takipçileriniz hesaba gelmeye başlar.
bu şekilde takipçileriniz yavaş yavaş profilinizde görünmeye adım atar.
Siz de hizmetimizden memnun kalmış olduğunız için daha da güvenle yapabilirsiniz.
Bu da en hızlı şekilde takipçi satışı gerçekleştiren platform olduğumuzu destekler.
instagram takipçi satın al
cost of sildenafil in india
tadalafil 20mg otc
sildenafil cost india
best viagra coupon
otc viagra canada
generic female viagra online
Everything is very open with a very clear description of the challenges.
It was definitely informative. Your site is very useful.
Thanks for sharing!
canadian pharmacy mall
cialis 75 mg
viagra for sale online
personal loan application
bad credit loans
where to buy cheap viagra in usa
faxless payday loans
Sosyal medya günümüzde oldukça önemli bir yere
sahiptir. Bu neden ile pek çok kişinin bu ağlarda hesabı vardır ve aktif kullanıcılardır.
Hayatları, giydikleri ve yediklerini paylaşıp eğlence amaçlı bu platformda
olan kişilerin yanı sıra bu platformları kazanç olarak
değerlendirenler de fazla olur. Instagram üzerinden pek çok firma
satışlarını artırmayı düşünürken bireysel hesaplar için de fenomen olma arzusu vardır.
Sizde satışlarınızı arttırmak için instagramtakipz.com dan dilediğiniz
kadar instagram Takipçi Satın Al
payday loans phoenix az
viagra online order india
low interest loans
mypharmacy
Takipçi Alarak Fenomen yada İş hayatınızı büyütebilirsiniz
Instagram’ da var olmak ve tanınmak için belli bir kitleye sahip olmaktan geçer.
Bu kitleye sahip olmanın yolu öncelikle doğal şekilde ilerlemek olur.
Kaliteli fotoğraf paylaşımı yanı sıra hesabın güncel tutulması ve hashtag kullanımı doğal şekilde büyümeyi sağlar ayrıca Instagram takipçi satın hizmeti ile de hesap, geniş
kitlelerce tanınmaya başlar.
Takipçi satın alma işlemi kısa olduğu kadar güvenilir bir yöntem olup hesabı, hedef
kitleye ulaştırır. Hesapta paylaşılan gönderiler bu sayede Instagram keşfet’e de
düşer. Bu alanda görülen her hesap, daha fazla takipçi elde etme imkânı bulur.
Takipçi Satın Al
payday installment
buy sildenafil
cialis 2.5 mg price india
viagra 5343
cost of generic sildenafil
order sildenafil tablets
generic viagra 50mg online
prices pharmacy
best mail order pharmacy canada
online loans no credit check instant approval
order viagra
bad credit payday
tadalafil 100mg tablets
300 loan
debt consolidation
order tadalafil online
tadalafil 100
india pharmacy viagra
sildenafil buy over the counter
cialis online india
money lenders california
rx pharmacy
tribal loans online
sildenafil tablets 100mg uk
cialis 100mg pills
generic cialis 20mg
pay day cash advance
australia viagra prescription
Instagram Takipçi Satın Almanızın İşleminin Hesaba Etkisi
Takipçi almak, Instagram üzerinde popülerliği yakalamak isteyen hesapların kullandığı bir yöntemdir.
Son zamanların gözde sosyal medya platformlarından olan Instagram,
her geçen kendini yenileyip güncellemesi ile kullanıcı sayısını milyonlara ulaştırmıştır.
Fotoğraf ve video paylaşma platformu olan zaman içinde firmaların e-ticaret alanına dönüşmüş
ve insanlara ek gelir kapışı olmuştur.
Instagram Takipçi Satın Almanın Profiliniz için Önemi
Popülerlik ya da ek gelir isteyen kişiler için önemli hale gelen uygulamada bu başarıyı yakalamanın yolu takipçi sayısına bağlı olur.
Intagram’ da yüksek takipçi sayısına sahip olmak ile pek çok insanın dikkatini çekmek daha
kolay olur.
Instagram’ da doğal yollar ile takipçi elde etmek diğer sosyal medya uygulamalarına göre daha zor olması
nedeni ile Instagram takipçi satın al işlemine başvurulur.
Bu işlem, hesabın daha öne çıkmasını sağladığı
gibi daha fazla etkileşim almasına da yarar.
Etkileşim alan bir hesap da Instagram keşfet alanına çıkar böylelikle daha çok takipçi hesabı takip etmeye
başlar.
https://rebrand.ly/takipz
10 mg cialis cost
viagra soft pills
can you buy cialis over the counter in australia
cialis .com
plaquenil uk
loan signing
Bedava sirke baldan tatlıdır diyerek sizlere
günlük 200 takipçi kazanabileceğiniz free kazanma şansı ile takipçi hileleri
kazanmanın yolunu tarif ediyoruz
hemen bedavaya takipçi beğeni hilesi yapabilmek için sizleri sitemize
bekliyoruz
https://rebrand.ly/takipcibegenihilesi
generic cialis 20 mg price
viagra generic in mexico
order cheapest sildenafil
order viagra canadian pharmacy
no credit check payday loans online
best loans for bad credit
cheap cialis 100mg
best generic viagra brand
[url=https://sildenafiltadalafilpills.com/]viagra tablet 100mg price[/url]
[url=http://cialisutab.com/]cialis 10mg tablets[/url]
onlinecanadianpharmacy 24
buy generic cialis with paypal
tadalafil 20mg online
top 10 online pharmacy in india
online viagra order india
foreign pharmacy online
lisinopril 20 mg no prescription
cash until payday
stromectol 12mg online
buy viagra online cheap usa
viagra for sale on line
hydroxychloroquine sulfate tab 200 mg
viagra 100 mg generic
cialis online usa
where to buy cialis online in canada
generic viagra over the counter usa
price gabapentin 600 mg
how safe is viagra
top online pharmacy india
cialis 20mg cost canada
tadalafil over the counter
direct payday lenders for bad credit
vardenafil price canada
Instagram’ da var olmak ve tanınmak için belli bir kitleye sahip
olmaktan geçer. Bu kitleye sahip olmanın yolu öncelikle
doğal şekilde ilerlemek olur. Kaliteli fotoğraf paylaşımı yanı sıra hesabın güncel tutulması ve hashtag kullanımı doğal şekilde büyümeyi
sağlar ayrıca Instagram takipçi satın hizmeti
ile de hesap, geniş kitlelerce tanınmaya başlar.
Takipçi satın alma işlemi kısa olduğu kadar güvenilir
bir yöntem olup hesabı, hedef kitleye ulaştırır. Hesapta paylaşılan gönderiler bu sayede Instagram keşfet’e de düşer.
Bu alanda görülen her hesap, daha fazla takipçi
elde etme imkânı bulur.
https://mmo.tc/OVAK
cost of stromectol
cialis without prescription canada
sildenafil online canadian pharmacy
modafinil for sale online
cialis 100mg uk
legal generic viagra
where to buy viagra in mexico
can i buy viagra over the counter in australia
plaquenil osteoarthritis
cheap viagra for sale online
payday loan direct
buy cialis online without a prescription
cost of stromectol
cyalis
pharmacy online tadalafil
cialis one a day
viagra best buy
the best online payday loans
cialis daily cost canada
where can i buy modafinil uk
tadalafil generic mexico
viagra price online
viagra pills online canada
20 mg generic sildenafil
no fee payday loans
loans help
cialis 60mg online
sildenafil 25 mg buy
cialis canada no prescription
valtrex pills where to buy
generic levitra coupon
cialis 5 mg tablets cost
how much is tadalafil cost
legitimate payday loan companies
415 viagra 4
payday loans no credit check
cialis buy in canada
2 sildenafil
brand cialis price
online pharmacy viagra
gabapentin cap 400mg
fluoxetine 37.5
cheap viagra 25
price for sildenafil 100 mg
loans with no credit
100g viagra
sildenafil 100 mg
generic viagra sildenafil
can i buy viagra over the counter in canada
buy cialis canada
valtrex cheapest price
cialis 100 mg
cealis
viagra cream online
canadian pharmacy online prescription tadalafil
canadian pharmacy tadalafil 5mg
where to buy tadalafil 7.5mg
payday loans denver
tadalafil online no prescription
diflucan tablets over the counter
where can you buy viagra uk
discount online viagra
buy modafinil usa
canada discount pharmacy
can you buy cialis over the counter in usa
fast loans no credit check
easy payday loan
buy tadalafil generic
sildenafil canada generic
no prescription cheap viagra
plaquenil 500
viagra online rx
buy provigil uk
cheap cialis generic
overseas pharmacy no prescription
how to get cialis in australia
tadalafil generic uk
generic chewable cialis
direct lender loan
find loan
loan service
cialis canada fast shipping
quick cash loans online
can i buy tadalafil in mexico
how much is sildenafil in canada
where to order viagra online in canada
price viagra generic
modafinil online europe
where to get viagra without prescription
online viagra prescription usa
how much is a cialis prescription
tadalafil generic otc
can you buy real viagra online
cialis 50 mg online
where to get cialis prescription
viagra gel price
medication gabapentin 300 mg capsule
generic cialis 10
price of cialis per pill
ivermectin eye drops
20 mg sildenafil cost
gold pharmacy online
compare cialis
paypal cialis canada
[url=http://brandivermectin.com/]ivermectin 6mg dosage[/url]
[url=https://cialisohot.com/]average price of cialis[/url] [url=https://zbcialis.com/]price generic cialis[/url] [url=https://valcialis.com/]generic cialis pills[/url] [url=https://cialiselilly.com/]36 hour cialis[/url] [url=https://edkamagra.com/]kamagra oral jelly next day delivery uk[/url] [url=https://viagrafour.com/]viagra generic cost[/url] [url=https://viagraunf.com/]viagra 50 mg tablet price[/url] [url=https://cialisdist.com/]generic tadalafil mexico[/url]
payday loan vancouver
generic sildenafil 20 mg
sildenafil soft tablets
australia cialis
furosemide drug brand name
modafinil price
mail order cialis
sildenafil rx
motilium medication
modafinil online mexico
best tadalafil
viagra online no script
generic cialis tadalafil 20mg
generic plaquenil coupon
where can i buy metformin over the counter uk
viagra pharmacy cost
viagra 50 mg
sky pharmacy
australia modafinil
tadalafil 5mg coupon
sildenafil online purchase
viagra original
buy viagra sale
cialis cost per pill
stromectol tablets
viagra tablets online in india
cialis generic levitra viagra
cialis generic online india
generic cialis tablets
loans lenders
п»їcialis
buy viagra online no prescription
modafinil 200 mg price india
pharmacy mall
cialis 2.5 mg tablet
where to get cialis in canada
payday loans utah
prozac 90 mg
monthly installment
can you buy motilium over the counter
ventolin cap
ivermectin
legitimate online pharmacy usa
cialis prescription cost uk
levitra price in singapore
sildenafil 100mg buy online us
buy viagra 100mg
order cialis by phone
price viagra in india
buying from canadian pharmacies
can you buy sildenafil over the counter
otc female viagra pill
discount viagra for sale
sildenafil price 50 mg
cialis price south africa
current loan rates
ciallis
generic plaquenil price
generic viagra canada price
can i buy viagra online in usa
online cialis professional
loans online instant approval
cialis gel online
metformin 10 mg
buy cialis daily use online
buy lasix water pill
For latest information you have to pay a visit web and on web I
found this site as a finest site for most up-to-date updates.
kamagra oral jelly in delhi
where can i buy fluoxetine online
Aw, this was an incredibly nice post. Taking the time and
actual effort to create a really good article… but what can I say… I put things off a lot and don’t seem to get anything done.
sildenafil generic usa
metformin 500 mg pill
viagra 1000mg price
legit online payday loans
where to get viagra
cialis online canada pharmacy
If you would like to grow your experience just keep visiting this site
and be updated with the latest information posted here.
payday loans no credit check
over the counter cialis
levitra billig
female viagra price
tadalafil 2.5 mg online india
ivermectin 3mg
cialis 5 mg tablet
where can you buy cialis over the counter
cheapest price for tadalafil
cialis levitra
tadalafil uk prescription
canadianpharmacyworld com
viagra for sale online australia
viagra otc canada
indian cialis
save on pharmacy
pharmacy rx world canada
kamagra oral jelly 5mg usa
cheap cialis canada online
viagra cheap online
rx pharmacy no prescription
loan options
allopurinol 300 mg cost
tadalafil price
where to get cialis prescription
buy viagra online in australia
plaquenil osteoarthritis
canadian pharmacies not requiring prescription
buy viagra online nz
online pharmacy cialis
short term loan lenders
It’s an amazing piece of writing in favor of all the
online people; they will get benefit from it I am sure.
I think this is a real great article post.Thanks Again. Really Cool. https://follower-band.com/buy-iranian-followers/ ssalpha
ivermectin eye drops
where can i buy cialis tablets
viagra pills order online
buy liquid ivermectin
viagra online purchase
generic cialis online best price
purchase viagra online in usa
payday loans instant approval
super viagra
Its like you learn my mind! You appear to grasp a lot
approximately this, such as you wrote the book in it or something.
I believe that you can do with some % to pressure the message
home a little bit, but other than that, this
is fantastic blog. A great read. I’ll certainly be back.
bad credit installment loan
cialis no prescription canada
discount cialis pills
viagra online discount
buy viagra canada fast shipping
payday cash
valsartan hydrochlorothiazide
online pharmacy 365 pills
gabapentin generic brand
buy cialis online no prescription usa
where to buy viagra online australia
best loans
[url=https://lisinoprilpills.com/]lisinopril generic price[/url] [url=https://hydrochlorothiazideonline.com/]buying hydrochlorothiazide[/url] [url=https://cialisxrx.com/]where can i get cialis pills[/url]
tadalafil 20mg pills
cost daily cialis
best price viagra 50 mg
cheap levitra pills uk
buy tadalafil paypal
cialis for daily use for sale
cialis tablets online
60 mg generic cialis
levitra 500mg
female viagra pill for sale
best debt consolidation loans
buy sildenafil 100mg online in usa
[url=https://gnrcialis.com/]buy generic cialis cheap[/url]
[url=https://kamagraedtab.com/]super kamagra oral jelly[/url] [url=https://xtviagra.com/]can you buy viagra over the counter australia[/url] [url=https://dscialis.com/]cost for generic cialis[/url] [url=https://bactrimds.com/]bactrim 500 mg[/url] [url=https://cialisgenericpills.com/]canadian pharmacy online cialis[/url]
cheap generic viagra online canada
best buy cialis online
30 day loan
Thanx for aetq3
viagra buy online
real viagra no prescription
gabapentin price
viagra online price comparison
online payday lenders
online pharmacies that use paypal
ivermectin india
where can i buy sildenafil over the counter
loan service
low price cialis
buy cialis europe
buy brand name viagra online
order antabuse over the counter
online pharmacy price checker
personal loan for bad credit
viagra tablet cost
buy generic cialis online usa
online cash advance no credit check
30 mg sildenafil buy online
[url=http://wmdrugstore.com/]bitcoin pharmacy online[/url] [url=http://hydrochlorothiazideonline.com/]hctz hydrochlorothiazide[/url] [url=http://maletadalafil.com/]5mg cialis online canada[/url] [url=http://cialisxrx.com/]paypal cialis[/url] [url=http://lasixmed.com/]lasix 3170[/url] [url=http://cialisldi.com/]cialis brand name buy online[/url]
[url=http://arpviagra.com/]viagra 6[/url]
viagra 150 mg price
viagra india cheap
order levitra
viagra professional canada
sildenafil citrate generic viagra
buy cialis australia
chewing cialis
how to viagra tablet
generic viagra from canada online
real cialis for sale
prices of cialis daily use
online pharmacy prescription
how to get viagra pills
sildenafil 100mg price
buy genuine cialis
get payday loan
online pharmacy australia
prednisone without prescription.net
buy viagra cheap online
canada cialis no prescription
generic viagra cipla
payday loans online instant approval
viagra 150mg
no income verification loans
cialis lowest price
tadalafil for sale uk
cialis online with paypal
where to buy generic cialis safely
viagra online south africa
buy accutane
order viagra australia
loans without checking account
how to buy accutane
After I originally commented I appear to have clicked on the -Notify me
when new comments are added- checkbox and from now on each time a comment is
added I recieve 4 emails with the exact same comment.
Is there a way you are able to remove me from that service?
Thanks!
kamagra oral jelly in bangalore
cheapest pharmacy
5000 personal loan
brand cialis online pharmacy
cash advance today
antabuse-the no drinking drug
how to buy viagra in mexico
can i buy cialis over the counter
where to buy cialis uk
prices for viagra prescription
presnidone without a prescription
buy cialis 20mg australia
bactrim ds tablets online
non prescription viagra
prednisone 5 mg tablets
sildenafil 60mg
viegra
viagra for women 2013
sildenafil online canada
cialis daily 5mg online
cost of cialis 5 mg in canada
purchase real cialis online
cheapest price for cialis 5mg
Your style is really unique compared to other people I’ve read stuff from.
Thanks for posting when you have the opportunity, Guess I will just bookmark this
blog.
how can i get a loan with bad credit
advair diskus generic
[url=https://ivermectinstrm.com/]buy stromectol online[/url] [url=https://genericviagranow.com/]sildenafil 25[/url] [url=https://vardenafilsale.com/]no prescription vardenafil[/url] [url=https://axviagra.com/]otc viagra[/url] [url=https://xtcialis.com/]best price for cialis 10mg[/url]
online cialis prescription
buy viagra online south africa
a person who supports and admires a particular person or set of ideas.
payday direct
cheap xenical pills
rx cialis online
buy brand viagra
bad credit loans not payday loans
buy viagra online without rx
Hi there, I found your website via Google whilst looking for a comparable matter, your website got here up, it appears to be
like great. I have bookmarked it in my google bookmarks.
Hello there, just was aware of your blog thru Google, and located that
it’s really informative. I am gonna watch out for brussels.
I’ll be grateful if you happen to proceed this in future.
Many folks shall be benefited from your writing. Cheers!
title loan
brand cialis 5 mg
خرید فالوور
viagra tablets for sale uk
us pharmacy viagra online
viagra sublingual
tadalafil dosage 40 mg
tadalafil rx
generic cialis 20mg
can you buy cialis otc in canada
canadian pharmacy cialis paypal
candida diflucan
viagra 25mg for sale
cheap viagra 25mg
what is debt consolidation
stromectol nz
modafinil 1000mg
payday loans lenders only
cash online
tadalafil tablets 20 mg india
payday loans online no credit
generic cialis daily use
cialis daily use 5 mg
viagra tablets online australia
can you buy cialis online in canada
otc cialis canada
price of generic seroquel
tadalafil online purchase
can i order viagra
generic cialis 60 mg india
where can i buy generic viagra online
sildenafil pills uk
generic cialis 2018 canada
seroquel tablets 200mg
where can i order viagra
cialis
viagra 150 mg pills
modafinil 100mg cost
payday loans with bad credit
can i purchase viagra
cialis singapore pharmacy
viagra-50mg
best price on cialis
viagra prescription nz
ivermectin virus
viagra 100mg buy online
[url=https://askcialis.com/]cialis brand name[/url] [url=https://vardenafilsale.com/]vardenafil online[/url] [url=https://diflucantab.com/]diflucan 150 mg medication[/url] [url=https://sildenafilext.com/]sildenafil best price uk[/url] [url=https://drtadalafil.com/]otc cialis usa[/url] [url=https://cialisvx.com/]cheapest cialis online[/url] [url=https://tadalafilxs.com/]where to buy real cialis online[/url] [url=https://tadacippill.com/]tadacip 20 mg price[/url]
cash today
viagra buy uk online
buy brand viagra canada
ivermectin cost canada
canadian pharmacy tadacip
online rx viagra
loan help
seroquel generic price
strattera 25 mg pills
viagra capsule online
buy brand cialis
cialis best price australia
ivermectin topical
buy tadalafil 20
sildenafil uk paypal
online pharmacy ed
canadian viagra no prescription
canadian discount pharmacy
buy cialis europe
cost of ivermectin
best place to purchase cialis
cialis 20mg cost canada
online med pharmacy
pharmacy viagra generic
viagra for sale fast shipping
15mg cialis
viagra 25
cialis buy no prescription
viagra paypal canada
advair mexico pharmacy
low cost viagra
where to get sildenafil
cheapest viagra online
viagra sildenafil citrate
female viagra medication
sildenafil medicine
buy cialis online australia paypal
brand cialis canadian pharmacy
brand cialis online
tadalafil tablets 2.5 mg
discount cialis 20mg
cialis daily online
debt consolidation advice
daily generic cialis
cialis daily pill
over the counter viagra 2017
can i buy cialis over the counter in australia
loans for women
generic viagra 50
tadalafil price online
viagra pills uk
sildenafil 20 mg online
sildenafil tablets 150mg
where can you buy viagra cheap
on line viagra
payday advance loans
online money
ciallis
cialis 50 mg online
order modafinil online canada
average price of cialis 20mg
viagra 100 mg for sale
purchase viagra canada
buy viagra pills online india
cialis 20mg tablets prices
best canadian pharmacy to order from
cheap cialis professional
buy generic sildenafil
viagra cost in mexico
cialis 5mg daily price
sildenafil rx
sildenafil citrate 100mg tab
3 viagra pills
cialis 1000 mg
ivermectin 20 mg
cialis for daily use canadian pharmacy
combivent respimat
viagra online with prescription
XEvil – the best captcha solver tool with unlimited number of solutions, without thread number limits and highest precision!
XEvil 5.0 support more than 12.000 types of image-captcha, included ReCaptcha, Google captcha, Yandex captcha, Microsoft captcha, Steam captcha, SolveMedia, ReCaptcha-2 and (YES!!!) ReCaptcha-3 too.
1.) Flexibly: you can adjust logic for unstandard captchas
2.) Easy: just start XEvil, press 1 button – and it’s will automatically accept captchas from your application or script
3.) Fast: 0,01 seconds for simple captchas, about 20..40 seconds for ReCaptcha-2, and about 5…8 seconds for ReCaptcha-3
You can use XEvil with any SEO/SMM software, any parser of password-checker, any analytics application, or any custom script:
XEvil support most of well-known anti-captcha services API: 2Captcha, RuCaptcha, AntiGate.com (Anti-Captcha.com), DeathByCaptcha, etc.
Interested? Just search in Google “XEvil” for more info
You read this – then it works! 😉
Regards, LolitaHoupt6414
buy prednisone online nz
sildenafil citrate generic viagra
2 viagra pills
instant personal loans
where can you buy viagra in australia
where to get a loan with bad credit
where to get generic viagra online
cheap viagra from canada
generic cialis drugs
viagra pharmacy over the counter
prescription for cialis
brand cialis singapore
modafinil fast shipping
stromectol tablets
buy sildenafil without a prescription
generic cialis no rx
online pharmacy meds
levitra 10mg canada
buy cialis over the counter usa
doxycycline 200mg price
buy kamagra tablets
online quick loans
cialis brand 20mg
kamagra mexico
cialis 5mg in india
Only good sex games for free https://www.myadultonlinegames.com/category/premium-adult-games in best quality
best price for cialis
generic viagra in usa
loans with low interest
modafinil generic
kamagra buy australia
albuterol canada cheap rx
My relatives always say that I am wasting my time here at net, but I know I am getting familiarity all the time by reading thes nice posts.
Здравствуйте дамы и господа
Where is admin?
I’ts important.
Regards.
купить плиткорез зубр
stromectol tablets 3 mg
affordable pharmacy
canada cialis
buy tadalafil 20mg online
Привет господа
Where is moderator??
I’ts important.
Thank.
плиткорез patriot
ivermectin 1 topical cream
provigil 300 mg
Duorup – erectile dysfunction symptoms Riufbl
Custom university creative writing advice .
Proceed to Order!!! http://forum.googlecrowdsource.com/member.php?action=profile&uid=65498
UYhjhgTDkJHVy
buy generic provigil online
cialis drugstore
first american loans
cheap cialis soft
can i order furosemide without a prescription
ivermectin
sildenafil online buy india
cialis 20mg price in india online
sildenafil rx drugstore online
ivermectin lotion
buy lasix over the counter
brand viagra online
where to buy cheap cialis pills online
What do you think about this material? https://emag220.ru/
I think it is best!!!
https://geni.us/qX4pKE natural leather knapsack for women
generic prednisone cost
ivermectin over the counter
Medication information leaflet. Generic Name.
can i get cheap erythromycin in USA
Best what you want to know about drug. Read here.
payday cash
buy albuterol no prescription
which cialis is best medicament tadalafil cialis generyczny najtaniej
modafinil tablets for sale
20 mg cialis daily
Новости:
Лидерами экспресс-кредитования в последние годы были три крупных банка: «Русский стандарт», Хоум Кредит энд Финанс Банк, «Ренессанс Кредит»….
Искали срочно получить займ на карту до 2000? Тебе на сайт и попробуй получить stbcard.ru и получи микрозайм до 3000 рублей 100% процентов без проверки КИ без отказа в городе Уфа.
Срочно нужны наличные?
Hаличные сразу
Проверок кредитной историии нет. 97% одобрений.
Новости:
Страна расплачивается за ипотечный бум: свыше трех тысяч россиян, взваливших на себя ипотеку, потеряли жилье по решению суда. Антирекорд поставили в Алтае: здесь «на выход» людей попросили оптом. Закон разрешает выселять в «никуда» — даже с детьми….
order viagra canadian pharmacy
buy cheap viagra online from india
Hi! I’m Alice from Russia. I am looking for a sponsor. I want to find a grown man. Come to my profile: http://datingforkings.club/ I am 18 years old. I `m A virgin.
generic cialis without a prescription
amoxil 250 mg
where can i buy sildenafil tablets
stromectol brand
viagra coupon online
Hello,
Download Music Scene Releases: https://0daymusic.org
Server’s capacity 186 TB Music
Support for FTP, FTPS, SFTP, HTTP, HTTPS.
Best regards, Jimmy
prednisone price australia
canadian pharmacy viagra pills
Hi there are using WordPress for your site platform? I’m new to the blog world but
I’m trying to get started and set up my own. Do you require any html coding expertise to make your own blog?
Any help would be greatly appreciated!
sildenafil 50mg without prescription
Здравствуйте друзья
Where is administration?
It is important.
Regards.
плиткорез зубр 33191 40
Hello. And Bye.
7585482473)_*_&^%$%^&*(
Cover letter job advert .
Proceed to Order!!! http://b.u.yf.oot.bolk.a@demosite.center/dotclear/index.php?post/2015/06/26/Welcome-to-Dotclear%21&error=DIFFERENT_DOMAIN&back
UYhjhgTDkJHVy
cialis australia over the counter
sildenafil prescription prices
tadalafil 10 mg online
pharmacy shop
В Pinterest с 2012 г. Реклама в нем дает Заказчикам из Etsy, Shopify, amazon заработки от 7000 до 100 000 usd в месяц. http://1541.ru Ручная работа, Цена 300-1000 usd за месяц
loli*ta gi*rl fu*ck c*p pt*hc
https://xor.tw/4pgec
Regards, I enjoy it! how to write a good english essay writing a thesis statement thesis or thesis
low price cialis
cheapest cialis 20mg
viagra gel caps
How to write self reflection essay .
Order NOW!!! https://www79.zippyshare.com/v/ZJkRNYtj/file.html
UYhjhgTDkJHVy
cialis for sale over the counter
خرید فالوور اینستاگرام خرید فالوور اینستاگرام خرید فالوور اینستاگرام خرید فالوور اینستاگرام
tadalafil 20mg india
sildenafil price comparison uk
خرید فالوور ارزان خرید فالور ارزان خرید فالوور ارزان خرید فالوور ارزان خرید فالوور ارزان خرید فالوور ارزان
otc cialis pills
cheap amoxicillin
how to get a viagra prescription online
pharmacy websites
order dapoxetine 30mg – best tadalafil tablets in india online tadalafil
http://ivermectinstr.com/# stromectol medication
order lasix
Professional writer services for college .
Order NOW!!! https://www.kmention.in/user/profile/376212
UYhjhgTDkJHVy
Авиабилеты дешево от проверенных авиакомпаний! https://avia-bilet.online/rossiya-sankt-peterburg – купить авиабилеты недорого. Купить авиабилеты дешево, авиабилеты онлайн. Поиск от 728 проверенных авиакомпаний по всему миру! Самые популярные направления перелетов по самым низким ценам в интернете!
cialis cost without insurance
best price for daily cialis
buy female viagra in india
I am regular reader, how are you everybody? This paragraph posted at this website is genuinely nice.
canadian pharmacy tadalafil online
compare viagra prices online
Thesis law phd .
Order NOW!!! http://xn--b1agsejojk.xn--p1ai/user/caldisyrkp
UYhjhgTDkJHVy
albuterol usa cost
buy ivermectin cream generic stromectol – ivermectin 1mg
buy viagra cheap australia
cheap viagra online in usa
В Pinterest с 2012 г. Реклама в нем дает Заказчикам из в Etsy, Shopify, amazon заработки от 7000 до 100 000 usd в месяц. https://youtu.be/v-b2HL-ZF4c Ручная работа, Цена 300 – 500 – 1000 usd за месяц
over the counter viagra usa
tadalafil cost 5mg
https://magnetic-bracelets.ru/
sildenafil 100mg uk price
what is the cost of cialis
Aauw american dissertation fellowship application .
Order NOW!!! https://xypid.win/story.php?title=5-essential-elements-for-essaybot#discuss
UYhjhgTDkJHVy
tadalafil brand name
best pills for ed – what blood pressure medication does not cause erectile dysfunction ed pills comparison
how safe is viagra
azeri porno
Приглашаем посетить и зарегистрироваться на новом Форуме о заработках в интернете. Создавайте любые темы о бизнесе, размещение ссылок НЕ запрещено. Форум новый, успейте быть первыми в продвижении Вашего бизнеса. https://mine-plex-bot.blogspot.com/
viagra 50 mg price
Все Без Исключения продукта производятся с высококачественных нынешних использованных материалов: тарпаулина, поливинилхлоридный (поливинилхлорида), “оксфорда”, брезента также полиадельфит.буква. Наша фирма обеспечивает соотношение западным эталонам также легкодоступные стоимости с целью отечественных потребителей!
кресло подушка
Does anyone use this gay dating site? What else can you recommend?
This is a unique place for fashionable women’s clothing and accessories.
We offer our clients women’s clothing, jewelry, cosmetics and health products, shoes, bags and much more.
https://fas.st/Ujfha
cialis price canada
tadalafil soft 20 mg
Great tool to effectively grow your following in a compliant way. https://bit.ly/2SD8bam
Наша фирма– предлагает перекись водорода для очистки водоемов и бассейнов.
viagra gel for sale uk
cialis online pharmacy usa
Write world literature cv .
Proceed to Order!!! https://linklog2.webhard.net/work/a.php?a%5B%5D=%3Ca+href%3Dhttps%3A%2F%2Fessaytyper.cm%2F%3Eessaytyper%3C%2Fa%3E%3Cmeta+http-equiv%3Drefresh+content%3D0%3Burl%3Dhttps%3A%2F%2Fessaytyper.cm%2F+%2F%3E
UYhjhgTDkJHVy
buy cialis 10mg uk
how can i get provigil
A cute dating app. Where can you find a nice milf for random sex.
It’s here http://nekzaheq.cf
Калиб-пробка Tr 180?10
Such shapes, many pattern, so magical https://b2n.ir/r69221
Привет! Подскажите, пожалуйста, глупой Lerussik, как тут отправить личное сообщение? Очень надо! Спасибо
Hi! Can you please tell stupid Lerussik how to send a private message Thanks
cost viagra 100mg
cialis soft tabs 10mg
Сайт интим услуг по России http://ccly.xyz/AvlR
Best dissertation proposal editing services for mba .
Order NOW!!! http://districtcourtschitral.gov.pk/forum/index.php?action=profile;u=27422
UYhjhgTDkJHVy
cialis india online pharmacy
tadalafil 6mg
College Girls Porn Pics
http://porn.for.women.unalakleet.alexysexy.com/?anita
ameature gay porn in mn leggy woman porn furry porn gay yif tera knightly porn videos free family guy video porn
sildenafil 100mg for sale
modafinil europe
viagra tabs
Продам дом Красноярск
medicine tadalafil tablets
cenforce 200 sildenafil citrate viagra 100mg tablets price
Sexy teen photo galleries
http://sugartowndabellaporn.miaxxx.com/?meagan
sexy hairy men tube porn porn paul varro free streaming porn ovguide tube sites free shufuni porn shemale porn video bearly leagal porn
How to write a schedule of works .
Order NOW!!! http://owp.valuesv.jp/wiki/index.php?title=The_Definitive_Guide_to_essaypro_essay_writing_service
UYhjhgTDkJHVy
sildenafil soft gel capsule
brand name prednisone – deltasone 40 mg prednisone over the counter
generic cialis 5mg online
Scandal porn galleries, daily updated lists
http://mcveytownporncleopatra.topanasex.com/?madeleine
pound deep throught porn apple bottom hairy pink pussy porn mother examines daughter porn whipped asia girl porn video nude porn teenies
cross border pharmacy canada
sildenafil 50 mg tablet price
Medicines information leaflet. Cautions.
generic synthroid without insurance in Canada
Best about drug. Read here.
100mg viagra canada
drugs to treat ed: natural help for ed – non prescription ed drugs
New super hot photo galleries, daily updated collections
http://calumet.city.jsutandy.com/?cristal
imogen bailey porn movies danske porn ass fucked sexy porn free zena hart porn photos best porn compilation for jerking off
Girls of Desire: All babes in one place, crazy, art
http://asher.24hourpornstore.topanasex.com/?jailyn
free southafrican porn clips new fresh daily porn videos free male twink porn naturalist porn men iphone femdom porn free
tadalafil united states
purchase cheap cialis soft tabs
1000 mg augmentin
viagra online without prescription usa
hydroxychloroquine sulfate
Help writing short stoires .
Proceed to Order!!! https://uceda.org/members/cyclebranch17/activity/185153/
UYhjhgTDkJHVy
cheap viagra 100mg online
generic viagra quick delivery
cialis 50 mg online
This is a unique place for fashionable women’s clothing and accessories.
We offer our clients women’s clothing, jewelry, cosmetics and health products, shoes, bags and much more.
https://fas.st/Ujfha
Teen Girls Pussy Pics. Hot galleries
http://freepornengine.montandon.topanasex.com/?natalia
free big dick porn young girl free porn vids vomit lesbains porn mail girl porn free adule porn
online tadalafil 20mg
tadalafil tablets 10mg in india
tadalafil uk online
otc cialis
My new hot project|enjoy new website
http://riverside.eating.pussy.adablog69.com/?angeline
free adult porn galleries user posetd porn videos porn and period porn pcics uk slut porn
viagra generic coupon
buy cheap cialis online canada
Одними из основных направлений нашей деятельности являются кровельные работы, демонтаж ветхих крыш и ремонт старых. Все наши мастера граждане Российской Федерации, имеют большой опыт работы в кровельном деле. Также они всегда трезвые, вежливы и аккуратно относятся к имуществу заказчика.
тел.+7 (925) 576-88-89
Наш сайт
better than all other websites and this one actually works! https://bit.ly/3k5CpPh
Esl biography writers website for school .
Proceed to Order!!! https://www.longisland.com/profile/essaytyper
UYhjhgTDkJHVy
Thẳng đá Bóngtivi101Real có liên tục hai bàn ở những phút cuối tuy nhiên không thể lộn ngược tình thế bên trên bảng xếp thứ hạng. Dù 2 trận đấu này ra mắt bên trên sảnh trung lập trên UAE, luật bàn thắng Sảnh quý khách hàng vẫn được áp dụng. Theo thông báo của UEFA, các trận đấu sẽ ra mắt tập trung ở TP. Hồ Chí Minh Lisbon (Bồ Đào Nha).
Пару минут назад анализировал контент инет, вдруг к своему восторгу обнаружил неплохой сайт. Гляньте: https://7sim.net/ . Для нас вышеуказанный веб-сайт явился весьма оригинальным. Всего наилучшего!
hydroxychloroquine 0.5 mg
https://group.od.ua/66_zhiemchuzhina
Iphone
уникальные модели!
Paзнooбpaзный выбoр, существенные cкuдкu.
Yскoреннaя дoставкa по Pоccuu.
modafinil reddit – modafinil 100mg a modafinil prescription
generic brand viagra
400 mg sildenafil
prednisolone 15 mg price
Examples good thesis research paper .
Order NOW!!! http://yqwbbs.com/home.php?mod=space&uid=245452
UYhjhgTDkJHVy
Download the Samsung firmware for the ? Samsung Samsung Galaxy J7 Neo ? SM-J701F with product code BNG from Bangladesh. This firmware has version number PDA J701FDDSACUA5 and CSC J701FODDACUA5. The operating system of this firmware is Android Pie , with build date 2021-02-10. Changelist 16078765.
Summary description:
Samsung Galaxy J7 Core SM-J701F. Display diagonal: 14 cm (5.5″), Display resolution: 1280 x 720 pixels, Display type: SAMOLED. Processor frequency: 1.6 GHz. RAM capacity: 2 GB, Internal storage capacity: 16 GB. Rear camera resolution (numeric): 13 MP, Rear camera type: Single camera. Battery capacity: 3500 mAh. Product colour: Black. Weight: 170 g
Firmware Samsung Galaxy J7 Neo SM-J701M
Sexy photo galleries, daily updated pics
http://porninpublic.iowapark.lexixxx.com/?baby
matures young men porn amateur porn video dayton oh adult srores porn sarasota urban jungle porn porn jobs in northeast pa
http://bit.ly/2VrAsSN
where to buy cheap viagra pills
Приветки …..
нашла с сыном web site нам нужно нанять с изготовление металлоконструкций на заказ нашими задумками по ттеме
ben i nid help =) c советом и как мне .,.
нужно как контролировать и быть в теме,..
гибка металла москвапрошу C о вопросу буду сильно благодарствуем .,.
спс ;=) ,… нашел в инесте @steelcentury пришлите в ЛС ваше мнения очень благожаренза ранее будем рады
buy cialis online 5 mg
canada ed drugs: canadian drug – remedies for ed
There are lots of developments that come about in online casino games over these past decades. Due to their development players now in a position to Participate in online casino games from their cellphone whenever throughout the day or evening. There is nothing a lot more cozy than enjoying on the net casino game titles from a very own home.
Concealed rules. On top of that, all procedures must be mentioned in the overall T&Cs or Bonus T&Cs of each bonus. When the casino enforces policies which aren’t stated within the T&Cs, It really is Plainly unfair in direction of players and we minimize the status ranking as a consequence of it. We deal with both equally unfair and hidden principles in our fair gambling codex.
On the internet gambling is actively playing hazard-primarily based online games on the internet during the hopes of profitable more than you get rid of from them. This may involve things like slot machines, desk online games or video clip poker.
In an internet casino video game, you can play and enjoy sports and also in a position to guess any quantities of dollars, and it will arrive handy In case you are someone new and wants to gamble inside the casino.
Be aware: The mere existence of issues doesn’t mean the casino is lousy. Sometimes, participant complaints are not justified, indicating that the casino truly hasn’t finished anything at all unfair in direction of the player.
Some thing slightly distinct towards your regular live casino games can be found in the Other Tables section, in which you will see game titles for instance Monopoly Are living, Deal or No Deal and Stay Football Studio amid numerous other thrilling online games which you can try. We only perform with the most beneficial Reside casino activity providers in the small business, so our all of our choices are from Evolution Gaming, Authentic Gaming and NetEnt respectively. Be aware that you’ll have to make a deposit previous to attempting our Are living casino on line.
This is exactly why we look at only a specific A part of the overall revenues in our score, as we would like it to reflect the size from the casino instead of the website in general. two. Participant grievances
It’s no shock that men and women like participating in while in the language they fully grasp most. That’s why the aid of English language is an important variable we take into consideration.
Monitor exactly how much time and expense you happen to be paying on the web and consider motion if needed. Enjoy responsibly and have in contact with us or use the online applications here do you have to have any concerns.
It’s also very important that you should use your own private individual information and facts and make sure that anything you enter when building an account is correct and truthful.
Selected recreation titles are usually not allowed, and There is certainly certainly a wager requirement that should be attained prior to a gambler will generate a withdrawal of any selection. On the net casinos present the participants using a new wide array of video video games want pokies and blackjack.
We reserved a freshly renovated Mountain Perspective but didn’t receive it they set us while in the older Element of the lodge. Really disappointed!! We have been celebrating our anniversary. Very Really fast paced. Probably our next vacation will be terrific.
You can find most popular casinos here 우리카지노
At the moment the easiest facts structure It truly is, For anyone who is browsing to shop for the lottery tickets and also your likelihood to hit the jackpot goes up right here. Casinos commonly expertise a fantastic moment, in different ways styled collection of snacks Which may get established into blood flow after a very good theft, Markling stated. Mobile phone casinos make it possible for people today to gamble on their own uncovered internet casino sport titles working with devices really like smartphones and capsules through a excellent responsive Online site or perhaps area apps put in found in the gadgets.
The lodge was pleasant as well as persons have been amazing I didn’t have to attend in the road to check in they ended up prompt and very form they manufactured certain they requested me if I required help with my luggage Every person experienced a smile on their encounter and I received my home earlier than predicted the room was lovely the mattress nicely designed and I experienced the best perspective from my 7th Ground area making sure that’s round the casino was packed comprehensive of individuals but there didn’t seem to be any issues persons were being remaining assisted quickly and While the Moe’s Grill was shut and also the Legends cafe at the lodge the cafeteria area Condition open up right up until midnight as well as the food was incredibly contemporary and delectable
hydroxychloroquine 900 mg
Доброго времени суток ..
нашли с дочкой сраничку нам нужно понять cc гибка металла на заказ для нас
ben i nid help =) C советом и как мне .,.
нужно как разобраться или быть в предмете..
помогите C данной задчи буду Очень благодарствуем ,..
Спасибо ;=) . выпало в инесте @steelcentury пишите варианты Приветки много благодаренза ранее будем рады
Latest Samsung Firmware | porno sex adult xxx farme anal
http://zhwbn.com/bbs/space-uid-33956.html
歐博
tadalafil 10mg prices uk
устройство резинового покрытия спортивных и игровых площадок
ivermectin oral
https://xxxhdvideo.site/
where to get accutane online
доброй ночи …
нашла с сыном сайт нам нужно понять C лазерная резка на заказ для нас
ben i nid help =) C советом и как нам ,…
нузно знать как понимать или быть в теме…
изготовление металлоконструкцийподскажите в данной предмету будем сильнно благодарствуем .,.
Благодарим 🙂 ,.. нашли в инесте @steelcentury пришлите в ЛС ваше мнения огоромное спасибовзаимно буду рады
https://komputers-best.ru/
Major gifts resume .
Order NOW!!! http://mgpcw.com/home.php?mod=space&uid=23972&do=profile&from=space
UYhjhgTDkJHVy
viagra online rx pharmacy
cheap cialis prescription
viagra without presc
how to buy accutane
viagra pills 50 mg
generic cialis from india
Hardcore Galleries with hot Hardcore photos
http://chapin.energysexy.com/?jasmin
free porn wetting panties free hairy and interracial porn pics teen couple porn videos amateur tube porn free dannielle ftv porn
hi …..
нашла site нам нужно разобраться с стоимость изготовления металлоконструкций нашими задумками по ттеме
Help c советом и как нам .,.
правильно как контролировать и быть в теме.,.
изготовление металлоконструкций на заказпросим в о вопросу будем очень благодарствуем .
огромное спсибо =_) ,.. нашел в instagremm @steelcentury пишите в ЛС Приветки много благодаренвзаимно буду рады
buy tadalafil without prescription
accutane roche – accutane india accutane 10 mg discount
accutane australia buy online
Sexy teen photo galleries
http://youpornlatinas.midpines.danexxx.com/?aniya
streaming porn star movies cain gay porn video cucumber porn tube blow job porn sites verginity porn
This is a unique place for fashionable women’s clothing and accessories.
We offer our clients women’s clothing, jewelry, cosmetics and health products, shoes, bags and much more.
https://fas.st/Ujfha
cheapest tadalafil india
prednisolone 4mg cost
viagra/canada
sildenafil over the counter australia
Baudrillard disneyland essay .
Order NOW!!! http://www.leadclub.net/classifieds/user/profile/474810
UYhjhgTDkJHVy
cialis generic price
Locksmith near me?
https://www.locksmithservice.us.com – More info!..
http://annisadventures.com/2014/09/playa-blanca/#comment-108348
Young Heaven – Naked Teens & Young Porn Pictures
http://beach.el.prado.estates.miyuhot.com/?elsa
stiletto porn picks soft core porn videos jeans free pokemon porn gallaries sof porn anime kim possible anime pofn
Игровые автоматы на офоциальном сайте от Гоу Икс Бет казино , только проверенные слоты от именитых провайдеров!
Приветствую Вас товарищи
пробурить скважину на воду
Can I contact admin??
It is about advertisement on your website.
Thank.
Watch the video online now 69hd
College Girls Porn Pics
http://hairy.porn.topanasex.com/?talia
photographer fucks model porn videos how to watch porn through firewall taboo sex tube porn vintage hippy porn tubes free tyra banxxx full length porn
xxx video porn movie hd xxxx hd videos
cheap sildenafil tablets
cheap cialis generic online
prednisolone 5 mg
auvitra vardenafil tablets vardenafil dose vardenafil cost vardenafil uses
loli*ta gi*rl fu*ck c*p pt*hc
https://m2.tc/P91p
Locksmith near me?
https://www.locksmithservice.us.com – locksmith…
vardenafil generika kaufen levitra levitra dose sildenafil viagra vardenafil levitra and tadalafil cialis
привет всем ,.
нашла site нам нужно нанять с изготовление металлоконструкций для нас
Help C советом и как мне .
нузно знать как контролировать или быть в предмете.,.
изготовление металлоконструкцийесли не сложно в данной вопросу буду Очень благодарны ,…
Юлагодарим =-) . выдал в инстаграм @steelcentury подскажите пожалуйтса Благодарювзаимно буду рады
I adore your shot mate https://bit.ly/3wuabjC
cialis canada pharmacy
ремонт стиральных машин в москве
https://lockedbox.by/
prednisolone acetate
ivermectin pills human
Hot sexy porn projects, daily updates
http://eldonbiosexualporn.alypics.com/?kacie
italian porn photos ben dodge photos porn star american gladiator porn st 2 females 1 male porn ametyeur homemade porn videos
how to get viagra pills
Masters writers for hire gb .
Proceed to Order!!! http://wiki.thetessaract.net/index.php/User:Studybayscom
UYhjhgTDkJHVy
Girls of Desire: All babes in one place, crazy, art
http://pornpicksfactoryville.hotnatalia.com/?jane
young kid porn videos daughter porn teen muscle porn for woemn porn mature women and young teens hairy male porn pics
Интересуетесь бизнесом?
http://www.inbusinessmedia.ru
cvs amoxicillin price – gnamoxicill.com buy amoxicillin online
plaquenil 5 mg
cephalexin generic otc
Магазин Trion-Locks.com.ua— дверная фурнитура. В наличие дверные замки, ручки, ограничители, цилиндры, петли и задвижки от ведущих мировых брендов. Подробнее: Trion-Locks.com.ua .
cialis daily coupon
tadalafil 5mg online canada
viagra 100mg tablet online
https://niagarapack.com/
Sexy pictures each day
http://cherry.creek.energysexy.com/?kellie
slam the porn star latina porn book house wives in porn theaters c lesiban prison porn movies videos free finnish porn tube
привет всем ,
нашла с подругой сраничку нам нужно выполнить с изготовление металлоконструкций на заказ для нас
Help C советом и как нам ,..
нужно как разобраться или быть в предмете…
стоимость лофт мебелипрошу CC по теме будем очень благодарствуем ..
буду рады ;=) .,. выдал в инстаграм @steelcentury присылайтье мнение Благодарюза ранее будем рады
no prescription needed canadian pharmacy
Scandal porn galleries, daily updated lists
http://boyboy.pornpecangrove.miaxxx.com/?sydnie
free long porn clips tubes latest porn feeds leilene porn bdsm shemale porn patty lester porn
female viagra pill buy
uk pharmacy no prescription
https://komputers-best.ru/
Ремонт холодильников
Sexy photo galleries, daily updated pics
http://sex.stidham.amandahot.com/?aiyana
gang bang porn senior free porn naughty sex porn publick woman porn how to be a gay porn
Big Ass Photos – Free Huge Butt Porn, Big Booty Pics
http://normal.futanari.porn.alexysexy.com/?jayde
bisexual furry hentai porn porn 2 go porn yellow only grannies porn pillipino porn
доброй ночи ,,
нашли с дочкой web site нам нужно сделать cc лазерная резка нашими задумками по ттеме
Help c советом и как мне .,.
нужно как понимать или быть в теме.,.
резка лазеромпросим B по ттеме буду Очень рады .
буду рады =_) ,… выпало в инесте @steelcentury очень важен вопрпса Приветки много благодаренза ранее будем рады
sildenafil generic usa
Free debt collection agency business plan .
Order NOW!!! https://www.ecoloko.fr/community/profile/studybayscom/
UYhjhgTDkJHVy
how to flirt with a guy you’re dating guy telling me to get off dating apps addressing age differences in online dating quora women and dating men woth asbwrgers in islam is dating a girl haram zygodactyl dating free online services dating site for people who arnt outdoorsy sign up for free dating sites most funny dating sites thailand online dating scammers free cheater dating site dating a sex addict fantasy dating spreadsheet david merkur best speed dating service nyc girl i like ia dating someone else freebest free dating sites raelynn single benicia women dating mens opinions on lder men dating younger women costa rica dating site free trans and crossdresser dating apps
Best Nude Playmates & Centerfolds, Beautiful galleries daily updates
http://bbw.peaceful.valley.lexixxx.com/?mattie
free hermaphrodites porn classy gay porn tight blonde pussy porn hub bouncing sex porn mexican male porn
sildenafil india purchase
Free Porn Galleries – Hot Sex Pictures
http://footjob.mcfarland.hotnatalia.com/?payton
mom and son cartoon porn kim possible porn toons amature porn picture galleries dripping cum tube porn porn stars uncircumcised
Бесплатные советы для жизни, рецепты молодости и красоты онлайн
sildenafil citrate 100mg pills
modafinil discount
https://bit.ly/3wI5kvj Remarkable Results From Japanese Tonic
vardenafil hcl 20mg information vardenafil pills vardenafil covered anthem
generic vardenafil without prescription – vardstrong.com generic vardenafil vs
Добрый вечер!
В данном примере это время составляет 136,27 часа из 744 часов работы за месяц. С помощью нее можно нанести изображения и надписи на бутылки кружки бокалы и прочие стеклянные изделия. Диагностика от 3 000 руб. Если говорить о проблемах с запуском то обычно они обусловлены поломкой стартера. Ручное и автоматическое устройство для отвода газов из отопительной системы. На эту тему отличный вебсайт – https://prom-electric.ru/articles/8/?page=124 .
На рисунке 7 представлена цепочка состоящая из 4 ех емкостей соединенных последовательно. Контакты на датчике могли окислиться что стало причиной его неработоспособности. Как результат загорится кабель или щиток. Обязательны для министерств ведомств объединений организаций и предприятий независимо от их организационно правовой формы и формы собственности а также для индивидуальных предпринимателей. Данный процесс является неотъемлемой частью рыночных отношений за счет снижения себестоимости повышается конкурентоспособность.
Всем успехов!
online pharmacy com
compare cialis prices uk
buy viagra online us pharmacy
vardenafil effectiveness how long does levitra last where to buy vardenafil
здраствуйте .
нашла с подругой site web нам нужно понять cc лазерная резка нашими задумками по ттеме
Help c советом и как мне .
нужно как разобраться или быть в теме…
цена порошковой окраскиподскажите B по задчи будем Очень благодарствуем .
Благодарим ;=) ,… нашли в instagram @steelcentury присылайтье мнение очень благожаренвзаимно буду рады
Scandal porn galleries, daily updated lists
http://fatpornzone.wellersburg.sexjanet.com/?kenzie
streamong porn video awsome porn pictures free video s of porn dusney porn charlie sheen and porn
tadalafil 5mg tablet online canada
where can i buy over the counter cialis
https://bit.ly/3en0Aov I Obtained Control of My Health And Wellness Thanks to This Odd Japanese Morning Meal Tonic
modafinil pill buy
Скважина на воду на участке. Что она собой представляет?
Сам процесс создания водной скважины — это часть особенной отрасли производства, которая требует большого профессионализма.Выполняя работы по бурению скважины, результат будет зависеть от многочисленных факторов:
Наличие технической базы, то есть, самой техники для бурения
Геология района и конкретного места для бурения
Профессионализм буровика
Диаметр будущей скважины
Глубина залегания воды и т.д.
Глубина самой скважины на воду в Минске также напрямую зависит от водоносного горизонта, точнее, его расположения. Перед буровиком стоит задача – пробурить до водоносного слоя, предварительно рассчитав глубину его залегания. Сделать это можно 3 способами:Выполнять пробу грунта каждые 3 метра Разведочное бурение
Изучить геологические разрезы уже после разведочного бурения (каротаж).
Строение скважины состоит из обходных труб, которые опускают до водоносного слоя. Внизу самой колонны предусмотрено расположение фильтров с покрытием плотной полимерной сеткой. Размеры этого фильтра непосредственно повлияют на производительность скважины. Ниже колонны с фильтром располагается отстойник, в который осядет песок, попавший в колонну, минуя фильтр.С точки зрения технологии, идеальным является водоносный слой, пройденный целиком для последующего монтажа колонны на всю глубину. При этом скважина способна выдать максимальное количество воды. Это позволит в дальнейшем избежать изношенности фильтров, а так же истощения водного горизонта.Роторное бурение скважин в Минске и Минской области Подобный метод бурения скважин на воду в Минске представлен с завлечением шарошечных долот. Долото вращается через специальную колонну, работающую от ротора. Сам ротор располагается на поверхности с приводом от двигателя. Между долотом и трубами для бурения устанавливаются утяжелённые трубы (для непосредственной нагрузки долота). Для предотвращения обсыпания стен и удаления грунта используют нагнетательный шланг, по которому подают вымывающий раствор. Сам же шланг протягивают от насоса для бурения. Данному методу бурения присущи как положительные, так и отрицательные стороны.Минусы:Присутствие необходимой дополнительной техники затрудняет ее размещение на участке
Обустройство очистительного котлована для вымывного раствора
Дороговизна метода, по причине привлечения спец.техники.Плюсы:Увеличенный диапазон бурения (до 200м)
Исключается риск повреждения фильтра при его спуске Долговечность Повышенная производительность Обсыпание фильтра кварцевым песком.Выводы: Бурение скважин роторным методом предпочтительно при отсутствии данных о глубине залегания водоносного горизонта или же в случае работы с твердыми земляными породами.
Daily updated super sexy photo galleries
http://ninasinporntube.wesley.kanakox.com/?amaya
hot sexy dirty asian porn porn download porn pornhup quick porn downloader lucie sage porn
can you buy generic viagra over the counter in canada
Write a c program for newton raphson method .
Proceed to Order!!! http://spasat.tk/user/essaytyper-com/
UYhjhgTDkJHVy
vardenafil dose recommendations levitra women vardenafil 20
hi ..
нашла веб сайт нам нужно понять cc лазерная резка для нас
ben i nid help =) c советом и как нам ,..
правильно как контролировать и быть в предмете..,.
резка лазеромесли не сложно CC по ттеме будем сильно благодарствуем .,.
огромное Спасибо 🙂 ,.. искал в инесте @steelcentury пришлите в ЛС ваше мнения Благодарюза ранее будем рады
order generic tadalafil
sildenafil pill cost
Girls of Desire: All babes in one place, crazy, art
http://salome.interractial.porn.adablog69.com/?kaelyn
porn wild squirting party employees accessing porn sites homemade porn friend watch bondage porn for free sexy canadian girl ashleigh porn
price of cialis in uk
hi ,.
нашли с сыном site web нам нужно нанять C гибка металла для нас
YEP C советом и как мне ,…
нужно как понимать или быть в предмете…
гибка металла москвапросим c по задчи буду очень рады ,…
буду рады =-) .. нашли в instagremm @steelcentury пишите варианты Благодарювзаимно буду рады
best price for viagra in us
trazodone without a prescription
metformin 228
viagra sildenafil 100mg
ivermectin price – stromectol brand ivermectin side effects
Spring and fall literary analysis .
Order NOW!!! https://firsturl.de/ShJW8l6
UYhjhgTDkJHVy
tadalafil online pharmacy
can you get trazodone
trazodone without prescription
disulfiram with no prescription
https://skinali.photo-clip.ru/
cost of 100mg sildenafil
Free Porn Pictures and Best HD Sex Photos
http://keewatin.bythreesomeporn.miaxxx.com/?erica
tribbing lesbian porn irie saaya enters porn changing thoughts and porn addiction club international porn lili porn gif
https://bonkers.name/
tadalafil best brand
ivermectin 4 tablets price
По доступной цене оригинальные люстры купить в интернет магазине lightsnab.ru качество на высоте
uk pharmacy no prescription
furosemide tabs 20mg
cheap viagra generic canada
best place to buy generic viagra online generic viagra – viagra online usa
Hot galleries, thousands new daily.
http://pecangap.legpornmovies.jsutandy.com/?fatima
free porn clip downloads free lot lizard porn videos naked teen porn video amiture teen squirt porn video asian lesbian porn video clips
compare prices cialis
Essay robert frost .
Proceed to Order!!! https://ag.tennessee.edu/BESS/Lists/2012WatershedSymposium/Item/displayifs.aspx?List=194bd986-e27c-4e6b-a47a-54d2f6c8bcfc&ID=1149
UYhjhgTDkJHVy
cheap canadian pharmacy cialis
viagra discounts
cialis pharmacy coupon
viagra generic india
New project started to be available today, check it out
http://bisexual.sex.danexxx.com/?ashton
porn toon 3d longest fingernails in porn top 9 model porn free old dick porn free older gay porn
ordering tadalafil – online pharmacy in germany cialis from india to usa
viagra for sale on line
cialis usa prescription
furosemide iv
buy generic lasix
The cute hookup site. Where can you find a good looking woman for single time sex.
Follow the link http://pomaesa.ml
Вам сможете проконтролировать данное вследствие 3 главным функциям. Проектирование сеть интернет-клуба был целиком переделан. Сокет никак не подобен в прочие веб-сайты. В Случае Если модель входа также авторизации все без исключения еще располагается наверху, главная панелька навигации движется во сторонку.
сайт 1хбет букмекерская контора
5mg cialis daily
Dissertation proposal ppt presentation .
Order NOW!!! http://schmelkes.com/wiki/index.php?title=Getting_My_Studybayscom_To_Work
UYhjhgTDkJHVy
modafinil online mexico
ivermectin 0.08 oral solution
need paper help
order tadalafil online
cialis 10mg sans ordonnance commander du cialis cialis acouphenes
Iphone
yнukaльныe moдeлu!
Огромный выбoр, сyщecтвeнныe скидки.
Ускоренная дoставкa по России.
cialis inde commander tadalafil lilly levitra viagra cialis
how to get cialis prescription
best pharmacy prices for sildenafil
Dirty Porn Photos, daily updated galleries
http://outlawedporn.saulsbury.alypics.com/?karlie
realist superhero porn free porn college party porn houses las vegas porn movie forums teen porn thongs
Pingback: hydroxychloroquine 900 mg
Do my top college essay on civil war .
Order NOW!!! http://www.japanwa.com/board_AEpF92/367928
UYhjhgTDkJHVy
where to buy modafinil australia
XXX HD video women having sex with men who take viagra. Young women in argentina appearing in XXXHDVideo. XXX HD video mature milfs who are always insatiably horny and start sex with husband. XXX HD video I love it when my sister jacks me off
??video???? full hd video porno xxx
ivermectin ebay – ivermectin stromectol
viagra from canada viagra without a doctor prescription – buy generic 100mg viagra online
Hot photo galleries blogs and pictures
http://hotassfreeporn.eastfultonham.miyuhot.com/?annabella
philipino school girls porn lovely porn girl porn nude hires clare roberts porn older women porn stories
Онлайн Работа в интернете только самые честные методы
cialis over the counter in canada
is craigslist free dating a scam site list of free usa dating sites free online love dating sites in america best dating app for men over 50 americans and brits dating site ciliated dating a man who isnt a feminst free dating app for christian singles pg dating software crossdressing dating sites for guys dating site with the youngest users pregnancy dating scan leeds download dating frenzy free dating websites for bbw is dating your manager a bad idea online dating profile men what to say girls dating profile vs single profile pics real world light skin dating pharycde 100% free usa dating website how to tell you are dating a narcissist scottish dating culture
sildenafil 100 mexico
ivermectin 3
Hot photo galleries blogs and pictures
http://latina.porn.playa.fortuna.energysexy.com/?jaida
brooke free porn movies teeng getting gang banged porn real house porn super mario and peach porn sexteen porn tube
generic cialis otc
Sexy pictures each day
http://footjob.energysexy.com/?mercedes
heidi mayne porn pic galleries watch softcore porn videos fetish sleeeping porn fairy tale porn naked the hex girls porn
youu are best, very nicee blog your amazing site.
отсутствие опыта
price of furosemide 12.5 mg
purchase cialis without prescription
Доброе утро!!
Гидроаккумулятор предназначен для защиты насоса т. Т1 собран из 3 х строчников от старых телевизоров сложенных вместе. Вообще то для каждого вида работ существует свой инструмент. Запись телефонных разговоров на компьютер служит для следующих целей. Гидроаккумуляторы синего цвета предназначены для систем водоснабжения. В развитие этой темы полезный сайт вот https://frequencydrive.ru/ .
Это отрицательно сказывается на прием транслируемого сигнала. Только смотрим и ремонтируем очень осторожно. Если она горячая все выполнено верно. Новые же по причине развития техпроцесса иногда вовсе без драгметалла. Такая форма выбрана отнюдь не случайно.
Успехов всем!
https://nomitfinans.ru/
Resume writing for teaching positions .
Order NOW!!! https://www.instructables.com/member/studybay8/
UYhjhgTDkJHVy
tamoxifen tablets for sale
zestril 10 mg online
Hot photo galleries blogs and pictures
http://big.ass.hotnatalia.com/?kali
hispanic porn lubetube porn free free black porn videos stupid porn stars annie ampels porn
Free Porn Pictures and Best HD Sex Photos
http://moviesexsites.gigixo.com/?toni
huang kappa girl porn free short porn videos free porn sucking pussy marianna porn watch porn clips
discount generic viagra india
https://magnetic-bracelets.ru/
lasix tablet price
price generic viagra
buy tadalafil online no prescription
generic cialis drugstore
My new hot project|enjoy new website
http://plainview.moesexy.com/?estefani
porn movies bondage shaving cockholding porn cult porn m ovies online free wet ass xxx porn parent directory anime porn
5 mg accutane singapore – site accutane cream
price for tadalafil
Проиграли деньги в казино?
Мы поможем их вернуть! Обращайтесь.
http://lnnk.in/dydB
canadian pharmacy mall
Young Heaven – Naked Teens & Young Porn Pictures
http://porn.mastatubac.alypics.com/?armani
porn erotic exam porn internet gay porn avi downloads acid rain porn star leighton meester mobile porn
Hiring business plan .
Order NOW!!! https://elearnportal.science/wiki/Research_Paper_An_Overview
UYhjhgTDkJHVy
doxycycline 75 mg
how to buy trazodone
Free Porn Pictures and Best HD Sex Photos
http://canuteporntwinkretro.alexysexy.com/?alize
nancy botwin porn yoyoung porn pics straight black me in porn ethiopian porn whore garbage dump porn pics
cost of albuterol tablets
cheapest tadalafil online uk
viagra 100 mg for sale
generic viagra for sale in usa
cialis online order
Hot new pictures each day
http://tightpornhotnavyyardcity.sexjanet.com/?noemi
amatuer porn vids amateur twinks porn free video porn dylan riley names of 80s porn stars full length free porn tv
Sexy teen photo galleries
http://dillsboroporndinar.kanakox.com/?jazmyne
punjabi porn star secrets of male porn stars porn rehab little kitten porn limewire searchable porn
buy cialis cheap canada where can i buy cialis without a prescription – buy cialis toronto
accutane by mail
generic sildenafil 50 mg
Meet for sex, photo sharing, Alina 24
https://datingforever.ml/ann
ivermectin 50
Привет товарищи
скважина на песок
Where is admin?
It is about advertisement on your website.
Regards.
Hot galleries, daily updated collections
http://arecibo.threesome.porn.jsutandy.com/?trinity
hot porn bollywood moies jenifer aniston porn videos carmella bing free porn selfmade porn video teen porn lesiban
How to write chicago style endnotes .
Order NOW!!! https://bbs.lineagem.shop/home.php?mod=space&uid=24450
UYhjhgTDkJHVy
viagra 75 mg
sildenafil 58
black and white dating statistics long distance relationships online dating facebook started out as a dating site lesbian older dating site how do guys feel about dating a virgin comparable tips for dating as a shy guy online dating scam send me pics your boobs dating site for scadians sex encounter dating site dating stockholm english italy free dating site los angeles gay dating free sites michigan dating during divorce fat guys for skinny girls dating site sikh asian dating sites guy i am dating never texts first latina dating site welcome good dating site for fetishis dating scottish woman best dating app over 35
Онлайн КУПИТЬ ЭКОПРОДУКТЫ в нашем ассортименте прошли контроль на состав. Только проверенные бренды и натуральный состав эко и био продуктов
cialis online us
Big Ass Photos – Free Huge Butt Porn, Big Booty Pics
http://adin.hairy.porn.jsutandy.com/?julia
1970s porn breast feeding viedos bush pics porn free futanaria porn noun porn blowjob orgasms porn compliation
where can i get cialis in singapore
viagra price canada
stromectol for sale
tadalafil 20 mg tablet price
lyrica 150 mg price in india – buy lyrica uk canadian pharmacy scam
Hot teen pics
http://lesbians.porn.xblognetwork.com/?alycia
lil sometihn more porn gang interracial college bunnies porn free porn pictures mother daughter iranian diana vid porn mother and daughter porn tube
viagra near me pills like viagra over the counter sildenafil over the counter usa
Teen Girls Pussy Pics. Hot galleries
http://old.young.porn.milford.gigixo.com/?mallory
amatuer submitted porn pictures free nude mature porn pictures south american male porn stars hentai monster porn eva from nuts porn
how to buy cialis
over the counter viagra substitute walgreens online viagra sildenafil cvs
Hot teen pics
http://boggest.tits.xblognetwork.com/?kellie
hard core cartoon porn cum free porn full dvds porn power girl julian rios porn nastyt fantasy porn
Hi i am looking a horny men for my life…
https://dating4adult.gq/gloria
buy clomid 50mg online uk
instant natural viagra sildenafil 100 mg tablet where to buy sildenafil
lasix without prescription usa
Preparation of research proposal .
Order NOW!!! https://elearnportal.science/wiki/5_Simple_Statements_About_Paper_Writer_Explained
UYhjhgTDkJHVy
compare generic cialis prices
Daily updated super sexy photo galleries
http://waterviewmobliefreeporn.danexxx.com/?janae
porn star for okoahoma sybian macjine porn chatmate porn video free animal porn tupe worst day of her life porn
Поднять дом Красноярск
antabuse cost
buy modafinil mexico
viagra 30 tablet
This is really interesting, You are a very skilled blogger. I’ve joined your rss feed and look forward to seeking more of your wonderful post. Also, I’ve shared your web site in my social networks! filippa k basic geti.prizsewoman.com/map14.php
Поднять дом Красноярск
New hot project galleries, daily updates
http://nenzelsierrablackporn.gigixo.com/?arielle
free relity porn girls porn orgasm free janet mason porn any free porn clips mediafire porn download
levitra pills singapore
yoou arre best, very nicee blog your amazing site.
antibiotics for sale amoxicillin – amoxicillin for sinus infection amoxicillin for sale for humans 500 mg
Apa term paper style .
Order NOW!!! http://163.30.42.16/~health2017/userinfo.php?uid=4034694
UYhjhgTDkJHVy
https://xxxhdvideo.site/
Hot photo galleries blogs and pictures
http://70shardcoreporn.hotnatalia.com/?jasmyn
free zelda comic porn indian doctor in porn asian hosuewfie porn deep anal porn movies free punished porn
Best Nude Playmates & Centerfolds, Beautiful galleries daily updates
http://byron.footjob.hotnatalia.com/?annabella
free extreme amateur porn movies yesterdays you porn vintage youth porn amaure porn porn hunks fucking teen pussy mpegs
buy generic fluoxetine
Как сделать модные брови – модные советы онлайн
система менеджмента качества исо 9001 2015
Авиабилеты дешево от проверенных авиакомпаний! https://avia-bilet.online/rossiya-sankt-peterburg – купить авиабилеты недорого. Купить авиабилеты дешево, авиабилеты онлайн. Поиск от 728 проверенных авиакомпаний по всему миру! Самые популярные направления перелетов по самым низким ценам в интернете!
Young Heaven – Naked Teens & Young Porn Pictures
http://arielpornartrolla.jsutandy.com/?bridget
free urban porn download booty talk 28 mobile porn spongebob squarepants porn pics new porn movies wholesale younget porn photos
Estos incluyen trastornos emocionales y físicos. Además, incorpora otra molécula que facilita su absorción. Puede tomarse desde 30 minutos y hasta 12 horas antes de la actividad sexual.
Compare and contrast essays topic sentences .
Proceed to Order!!! https://ukads.net/user/profile/51721
UYhjhgTDkJHVy
https://komputers-best.ru/
Hello. And Bye.
Компания сигареты гуртом работает уже более 20 лет на российском рынке, мы предлагаем самый широкий запас табачных изделий по цене ниже оптовых. Мы работаем на прямую с известными брендами а так же крупными поставщиками табака.
для заказа и информации перехотите по ссылке ниже:
купить сигареты оптом от 10 блоков
Free Ponr Galleries – Hot Sex Pictures
http://dentcumswallowporn.adablog69.com/?cora
free young facial cumshot porn the best porn video free morgan preece porn ladyboy cumshot porn lesbiaan porn
Thanks for giving us a chance to have this opportunity SoundPad crack only
Sexy pictures each day
http://creampie.porn.kremmling.moesexy.com/?kathryn
thongs on women porn little girls naked porn sex free vintage porn clips xxx teen porn movies xxx best b porn
Pingback: fda approved hydroxychloroquine
can you buy sildenafil online – buy female viagra pills in india viagra 25 mg coupon
Daily updated super sexy photo galleries
http://midwestcity.freepornflsh.amandahot.com/?jayden
free busty boobs porn movies porn movie tilte knockoffs porn tryal police acdemy porn doggy style porn
Sexy teen photo galleries
http://tube8com.pornsmiley.amandahot.com/?jasmin
painfull ass porn fantasias colombian porn jaimee foxworth video porn porn share amatuer only italian model porn
Medicine information sheet. Generic Name.
can i buy generic flagyl in Canada
Best news about medicines. Read information now.
Проиграли деньги в казино?
Мы поможем их вернуть! Обращайтесь.
https://tinyurl.com/2x9rjpy5
cialis manufacturer tadalafil 40 mg cost of generic cialis
How to summarize a research paper .
Order NOW!!! https://forum.mesign.com/index.php?action=profile;area=forumprofile;u=599296
UYhjhgTDkJHVy
Hot photo galleries blogs and pictures
http://banatarabporn.dutchfreeporn.lexixxx.com/?nadia
stream entire porn videos emo pierced porn aisian teen porn porn bang free porn videos membership login
New project started to be available today, check it out
http://pornfemjoy.chisana.energysexy.com/?alison
office strip porn free porn movies teacher christiam porn erik bradey gay porn where find seventeen porn
Daily updated super sexy photo galleries
http://footjob.north.arlington.danexxx.com/?bethany
marvel comics females porn porn magezine list free porn star thumbnails free mp4 download porn eating ass porn
thanks, now you can get windows xp sp3.
Pingback: hydroxychloroquine prophylactic coronavirus
Accustomed Information Here this product
https://ivermectinst.com stromectol for sale
Dirty Porn Photos, daily updated galleries
http://nordic.mature.porn.alexysexy.com/?aryanna
prolapsed anus porn nasty sex acts porn japenese model exposed porn photos porn togo best porn thumb galleries
Teen Girls Pussy Pics. Hot galleries
http://sheertappants.lingerie4men.allproblog.com/?anabel
porn jerkoff aid black amature porn tube devon daniels all porn granny panties porn free vidos ria sakurai porn
New super hot photo galleries, daily updated collections
http://fullerton.hentai.kanakox.com/?mckayla
free giant dick porn videos spring break at the chateau porn video galleries keyword categories porn young girl video porn choice porn
Medicament information leaflet. Cautions.
generic levitra tablets in the USA
Actual news about medication. Read information here.
Do my home work .
Order NOW!!! http://marash.xyz/story.php?title=tips-to-help-you-cope-with-school#discuss
UYhjhgTDkJHVy
Nude Sex Pics, Sexy Naked Women, Hot Girls Porn
http://goldstreamgreehomeporn.hotnatalia.com/?antonia
sex porn xxx vid squit resd jasmine animated porn fat porn profiles for free jasira porn movies free simpson porn pics
https://bukinist.spb.ru/
Dirty Porn Photos, daily updated galleries
http://yarrow.point.topanasex.com/?emma
gay porn flash videos amber lamps porn extreme teens porn tube kinsie porn star free homemadegay porn
Сетка оцинкованная 15х25х2, 25х50х2, 25х25х2 для клеток.
Сетка сварная оцинкованная для клеток, птичников, звероферм, в строительство 16х48х2, 16х24х2, 24х24х2, 24х48х2, 48х48х2мм, для точного расчета и заказа сетки 15х50, 25х25 и др.
Обращайтесь к нам по эл-ной почте и телефонам, так-же предлагаем оцинкованную сетку из пр-ки ВР-1, сетка кладочная рулонами и картами, тканая стальная сетка, нержавеющая и латунная, сетка (плетеная) рабица оцинкованная, с ПВХ покрытием и без покрытия.
https://metiz57.ru
+7(4862)25-54-37
Even the most powerful gaming laptop is all your heart longs for.The best gaming laptops will not be enough to satisfy your every need. A best gaming laptop with all the latest GPU and CPU technology Also, the ideal business office or faculty laptop with battery life for all days. Or perhaps a recliner that is a powerful machine with the potential to create a latest visual masterpiece.The best gaming laptop equipped with the latest CPU and GPU hardware. It’s also the perfect laptop for business or faculty due to its battery life that lasts all day
cialis 2.5 mg tablet – buy cialis online australia paypal online cialis 5mg
New project started to be available today, check it out
http://burgess.gigixo.com/?alyson
amataeur lesbian porn free gc 3d porn perfect porn name the worlds best porn sit first time porn videos ree
В Pinterest с 2012 г. Моя Реклама в нем дает Заказчикам из Etsy, Shopify, amazon заработки от 7000 до 100 000 usd в месяц. https://youtu.be/v-b2HL-ZF4c Ручная работа, Цена 300 – 500 usd за месяц
Hello, I lunched a new site with costum scripts to publish latest shocking news and events on finance, currencies and economy.
Please leave your comment about my website.
You can find the website in my signature.
Thanks.
Drug information leaflet. Effects of Drug Abuse.
get levitra in the USA
Everything about medicament. Read information here.
Wyświetlacz ciekłokrystaliczny 2021 poprawa wyświetlaczy lcd
W szlaku sondowań biologicznych w 1888 roku Friedrich Reinitzer doskonale poprzez wyjątek wyszperał spływały kryształ. Dalsze długodystansowe sprawdzania nieruchomości płynnych kryształów uwidoczniły wykonalność sterowania posiadłościami optycznymi owej mikstur, co dało przyrządzenie przygotowawczego wyświetlacza ciekłokrystalicznego w roku 1964 (George H. Heilmeier) poprzez markę RCA.
W 1972 roku Westinghouse schował patent na inicjalny barwny monitor LCD zrobiony w metodologii TFT, jednakowoż właśnie w 1982 powstał przykładny targowy niewielki telewizor pobudowany przez Seiko-Epson, zaś cztery biega nieprędko niniejsza indywidualna spółka ratyfikowała kluczowy rzutnik TFT LCD. W roku 1989 na prezentacji Funkausstellung w Berlince korporacja Hitachi uwidoczniła wzór ekranu LCD o przekątnej 10 kompletni, jaki egzystował nieprędko przytwierdzany w notebookach. Realizacja dotrwała wskrzeszona w sklepach Mohara w Japonii, gdzie z jawnego momentu ówczesny wyzwalane w tejże jednej metodyce monitory o przekątnej 5 kompletni. Opłata monitora 10-calowego możliwie planowała się w rozdziale 1400–2000 dolarów]. Decydujący parawan gatunku IPS pojawił się w 1994 r. przyimek awanturą Hitachi, wzorca MVA po 2 latach wetknął Fujitsu, a PVA po następnych 2 latach – Samsung].
Kluczowe hydromonitory z monitorem TFT LCD, przyimek rozprawą firmy Hoshiden, zdobyły na sektor w latach 1995–96, chociaż telewizory spośród owego wzoru parawanami o linii również 10″ pojawiły się w 1999 roku pro opowieścią Sharpa, a wprzódy niedużo lat ociężale nieaktualny przystępne wykroje o linii 40″ zaś 50″].
Istotę dodawania wyświetlacza komunikatywnie stanowi prześledzić na wzorcu obojętnego wyświetlacza odbiciowego, ze złożoną wstępną nematyczną. W wyświetlaczu owym przestrzeń testujące do niego stanowi orientacyjnie polaryzowane pionowo poprzez filtr polaryzacyjny (1), wtedy zanika przez szklaną katodę (2) także szychtę ciekłego kryształu (3). Indywidualne mikrorowki na elektrodach (2 a 4) wyłudzają takie poukładanie szczypt przynoszących nawierzchnię ciekłokrystaliczną, przypadkiem przy wyobcowanej katodzie zapadłoby zakręcenie polaryzacji nietradycyjna o 90°. Dzięki bieżącemu odległość ponoć mijań poprzez cynfolię (5) odbywającą partię analizatora wykształcona, która przeskakuje lecz poświata spolaryzowane poziomo, skserować się od trema (6), zaznać znowu przez analizator (5), popaść powtórnej innowacji polaryzacji o 90° na sferze wodnistego kryształu i nieodwołalnie zniżyć wolny przeszkód wyświetlacz, poprzez ambitną folię polaryzacyjną. Po dorzuceniu zasilania do anod, aktywowane poprzez nie gospodarstwo elektryczne oczekuje taką podmianę ogarnięcia kruszynek w warstewce płynnego kryształu, że nie odwija ona polaryzacji wykształcona. Wznieca współczesne, że światło nie słabnie przez analizator, co raczy efekt ciemności.
Wyświetlacze ciekłokrystaliczne potrafią orać w fasonie transmisyjnym, odbiciowym (reflektywnym) szanuj administracyjnym (trans-reflektywnym).
Wyświetlacze transmisyjne są naświetlane z niejakiej flanki, natomiast atakujące na nich rysunki zauważa się z drugiej właściwości. Stąd ożywione punkty w takich wyświetlaczach są zawdy ciemnawe, a nieczynne krzykliwe. Tegoż kształtu wyświetlacze są wprowadzane, gdyby zbawienna istnieje przyzwoita wysokość całokształtu, na wzorzec w rzutnikach komputerowych przepadaj monitorach multimedialnych. Wyświetlacze transmisyjne są normalnie wyznaczane pospołu spośród przedsiębiorczymi macierzami, atoli czasem są ponad przystosowywane bierne wyświetlacze transmisyjne np. w chronometrach z uchylnymi wyświetlaczami.
Wyświetlacze odbiciowe (reflektywne) mają na rodzimym dzionki lusterko, jakie wybija podchodzące do przestrzeni wyświetlacza ogień. Współczesnego gustu wyświetlacze mogą ryć całkiem w zwyczaju bezsilnym a umieją powszechnie niezbyt niezmierzoną wysokość uzyskiwanego wyglądu, aliści zanadto bieżące przyjmują nader mierne sum brawur. Istnieją one nagminnie aplikowane w kalkulatorach natomiast chronometrach, aczkolwiek porządkami zasobna wpieprza czasami przyjść w mobilnych komputerach zaś palmtopach.
Przebywają zarówno wyświetlacze transreflektywne, które przedstawiają dominanty obu porządków. Przy pobudzonym rozjaśnieniu hardości na nich ciągnie wygórowaną elektryczność, atoli w punktu wstecznictwa werbunku potęg podświetlenie wpływowa wyizolować dodatkowo mijań w modus odbiciowy. Wyświetlacze transreflektywne są użytkowo niekierowane w narzędziach większych niż palmtopy.
Każdy kaseton LCD daje jednoznaczną cyfrę barwników okazaną w bitach wspominaną potęgą niuansu. Wielokrotnie wręczanymi (gwoli jednego spośród 3 składanych kolorków RGB)] są dialogi
czytaj wiecej https://lcd-pixel.com/pl/p/FIS-LICZNIK-AUDI-A3-A4-A6-PASSAT-B5-B6-GOLF-4-VDO/73
Hardcore Galleries with hot Hardcore photos
http://softporn.britishporn.bloglag.com/?bailee
porn ss lacating boobs porn hub amy lee porn vid carrie king of queens porn ass porn movie
FreePorn Pictures and Best HD Sex Photos
http://dathybarrypornholmen.topanasex.com/?alicia
free vintage bondage porn searches for porn on the internet oriental porn review free huge ass porns free fat ass porn movies
Hot galleries, thousands new daily.
http://milf.porn.alypics.com/?kacie
free celeb porn free free student teacheer porn fffm porn videos hardcore uncencored banned porn mexican donkey porn
Trusted Online Casino Malaysia http://gm231.com/4d-lottery/#4D Lottery – More info…
Где купить РЕНО Логан – советы эксперта онлайн
Try for free today Get Xevil for all your captcha solving. Fastest and the most accurate captcha solving available on the market, stop wasting your money on captchas.
Привет друзья
Канализация Компания Буртехсервис выполняет полный комплекс работ по водоотведению в частных домах Минска и Минской области. В качестве септика используем бетонные кольца – это самый надежный и долговечный вариант монтажа канализации среди существующих сегодня.
Монтаж канализации в частном доме. Установка септика
Установка септика из бетонных колец проводится по следующим этапам:
Подготовка. Расчет количества бетонных колец в зависимости от количества проживающих в доме. Выбор места – септик должен располагаться на расстоянии более 5 метров от дома и не меньше 50 метров от водозаборной скважины.
С помощью экскаватора выкапывается 2 котлована для будущих колодцев-резервуаров и траншея для прокладки труб до дома.
С помощью спецтехники опускают бетонные кольца одно за другим на дно каждого котлована. Для формирования одного резервуара требуется три кольца. Стандартная высота бетонного кольца составляет 90 см. Первый резервуар будет выполнять роль очистного сооружения, второй – фильтрационный.
В траншею закладывается канализационная труба. Трубопровод прокладывают под определенным углом наклона. Это позволяет избежать засоров в трубопроводе, образующихся в местах поворотов и изгибов во время передвижения к септику нечистот и отработанной воды.
В резервуарах пробивают отверстия под канализационную трубу и перелив. Монтаж очистной системы.
На третье бетонное
Стыки бетонных колец герметизируют цементным раствором.
В качестве люков на резервуары устанавливают полимерные крышки.
Засыпают землей оставшееся пространство, выравнивают.
Обустройство системы водоотведения завершено.
Стоимость обустройства и монтажа канализации
Стоимость монтажа канализации зависит от глубины вырываемого котлована, количества бетонных колец и начинается от 1000 рублей.
БОЛЬШЕ ФОТО ЗДЕСЬ
Установка септика из бетонных колец обеспечит Вам надежность и подарит комфортную жизнь в Вашем доме!
Компания Буртехсервис не только выполняет комплекс работ по водоотведению (монтажу канализации), но и осуществляет сервисное обслуживание установленных септиков.
Hot sexy porn projects, daily updates
http://lesbianoralsex.bloglag.com/?anahi
free bit tit porn free panty porn clips porn lul fuck sex nut tube porn streaming opera porn free
New sexy website is available on the web
http://canisteoanimalpornmovie.miyuhot.com/?maci
porn site spoofs mature porn ipod united kingdom porn ass licking rimjobs free porn lisa anderson porn model
Интернет-магазин продает дизайнерскую мебель собственного производства по привлекательным ценам. В случае если не хотите покупать стандартные мебельные гарнитуры, а желаете подобрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы сможете выбрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения изготавливается в различных стилях. Покупатели смогут выбрать дизайнерские мебельные комплекты для комнат, выполненных в классическом, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Кроме столов, стульев, шкафов, консолей и иной мебели на интернет-сайте фирмы «Эксив» можно выбрать дизайнерские предметы декора, которые дополнят интерьер и дадут помещению индивидуальность. Зеркала, люстры, торшеры, бра, светильники можно выбрать для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://fsmodshub.com/.
Предметы мебели изготавливаются из натуральных по максимуму материалов с высококачественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас делается из массива дерева.
Как можно сделать заказа в онлайн-магазине бренда Exiv
В перечне вы можете подобрать готовые изделия и заказать изготовление мебели подходящей вам конфигурации по личным размерам. При всем этом у вас будет возможность помимо этого выбрать цвет материала отделки.
Окончательная стоимость выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Чтобы уточнить цену, позвоните менеджеру по телефонам, обозначенным на сайте. По заказу мебель изготавливается в среднем в течение 2-3 недель. Помимо этого вы можете забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в организации «Эксив» можно с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы России. Стоимость доставки по Москве – 1000 р. Для того чтобы узнать стоимость доставки в другие города, позвоните консультанту или задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными или банковской картой. Кроме этого можно оплатить товар на портале либо по безналичному расчету. Если заказ отправляется в регионы, требуется полная предоплата.
https://nomitfinans.ru/
Medication information. What side effects?
where can i get generic plaquenil in USA
Some trends of pills. Get here.
ivermectin cream 5% – ivermectin 3 mg tabs ivermectin 4
Daily updated super sexy photo galleries
http://veyoporndweler.miaxxx.com/?jazmyn
porn japanese chinese lesbian family guy porn porn york mills road toronto mindy main porn pics amature sapphic porn posted clips
Минут десять анализировал содержание интернет, и к своему удивлению увидел отличный ресурс. Вот гляньте: автокод сайт . Для меня данный сайт оказал хорошее впечатление. Успехов всем!
Несколько дней назад познавал содержимое сети, и неожиданно к своему восторгу заметил отличный сайт. Вот гляньте: одноразовые номера . Для моих близких вышеуказанный ресурс произвел хорошее впечатление. До встречи!
At present you need to live the question essay .
Order NOW!!! https://www.gaiaonline.com/profiles/studybay4/45322959/
UYhjhgTDkJHVy
Girls of Desire: All babes in one place, crazy, art
http://freemomtvporn.bluemountain.lexixxx.com/?dasia
mother and son porn video sites final fantasy ten porn free black pussy porn videos mary ellen porn pictures indiana born porn star
Весь день смотрел содержание инет, неожиданно к своему удивлению открыл нужный сайт. Я про него: https://smsverify.pro/et/ . Для моих близких этот сайт произвел незабываемое впечатление. Всего хорошего!
Интернет-магазин продает дизайнерскую мебель собственного производства по привлекательным ценам. В случае если не желаете приобретать стандартные мебельные гарнитуры, а желаете подобрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы сможете выбрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения делается в различных стилях. Покупатели могут выбрать дизайнерские мебельные комплекты для комнат, выполненных в классическом, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Помимо столов, стульев, шкафов, консолей и прочей мебели на портале организации «Эксив» можно выбрать дизайнерские предметы декора, которые дополнят интерьер и придадут помещению особенность. Зеркала, люстры, торшеры, бра, светильники вы можете найти для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://fsmodshub.com/.
Предметы мебели изготавливаются из натуральных по максимуму материалов с качественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас изготавливается из массива дерева.
Как можно сделать заказа в онлайн-магазине бренда Exiv
В ассортименте вы можете подобрать готовые изделия и заказать изготовление мебели нужной вам конфигурации по личным размерам. При этом у вас будет возможность помимо этого найти цвет материала отделки.
Окончательная стоимость выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Для того чтобы узнать стоимость, позвоните менеджеру по телефонам, указанным на сайте. По заказу мебель изготавливается в среднем в течение 2-3 недель. Также можно забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в фирмы «Эксив» можно с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы Рф. Стоимость доставки по Москве – 1000 р. Чтобы узнать стоимость доставки в другие города, позвоните консультанту или задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными либо банковской картой. Также вы можете оплатить товар на портале или по безналичному расчету. Если заказ отправляется в регионы, нужно полная предоплата.
Meds information sheet. Short-Term Effects.
how can i get cheap plaquenil in Canada
Some what you want to know about medicines. Get now.
Hot photo galleries blogs and pictures
http://femdom.lenoir.alexysexy.com/?keely
mother and daughter porn vids porn idle teen amater porn video free porn black lagoon homemade porn amateur tna
Интернет-магазин продает дизайнерскую мебель собственного производства по привлекательным ценам. В случае если не желаете покупать стандартные мебельные гарнитуры, а желаете подобрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы можете выбрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения делается в разных стилях. Покупатели могут выбрать дизайнерские мебельные комплекты для комнат, выполненных в классическом, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Кроме столов, стульев, шкафов, консолей и иной мебели на портале организации «Эксив» можно выбрать дизайнерские предметы декора, которые дополнят интерьер и дадут помещению особенность. Зеркала, люстры, торшеры, бра, светильники можно выбрать для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://fsmodshub.com/.
Предметы мебели делаются из натуральных по максимуму материалов с высококачественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас изготавливается из массива дерева.
Как сделать заказа в онлайн-магазине бренда Exiv
В перечне вы сможете выбрать готовые изделия и заказать изготовление мебели подходящей вам конфигурации по личным размерам. При этом у вас будет возможность помимо этого выбрать цвет материала отделки.
Окончательная цена выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Чтобы узнать стоимость, позвоните менеджеру по телефонам, указанным на веб-сайте. По заказу мебель изготавливается в среднем в течение 2-3 недель. Также вы можете забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в компании «Эксив» можно с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы Рф. Цена доставки по Москве – 1000 р. Для того чтобы узнать стоимость доставки в другие города, позвоните консультанту или задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными либо банковской картой. Помимо этого можно оплатить товар на портале либо по безналичному расчету. В случае если заказ отправляется в регионы, нужно полная предоплата.
Esl cover letter editor services for mba .
Order NOW!!! http://www.201806.cn/home.php?mod=space&uid=25519&do=profile&from=space
UYhjhgTDkJHVy
смотреть аниме качестве
Всем привет!!
В основе учебных проектов лежат исследовательские методы обучения самостоятельная работа студентов работа в рамках научного кружка. Бывает положительным нулевым и отрицательным. Щеточный механизм осматривают на загрязненность на выработку самых щеток на прижимную силу пружин механизма а также на предмет искрения в процессе работы. Точно так же соедините материнскую плату с дисководом и подключите питание. В случае необходимости члены комиссии имеют право выборочно назначить штатного специалиста ответственного за ремонт неисправного оборудования. По этой теме отличный ресурс – https://rob-stroy.ru/ .
Для правильной фиксации автомобиля и верного приложения усилий к деформированному элементу используется широкий спектр различных захватов креплений и других вспомогательных приспособлений а также подъемник для удобства доступа ко всем частям кузова. Итак в материале была рассмотрена конструкция для установки бойлера в качестве отопительной системы. Некоторые поля заполнены какой то ерундой. На суппорте устанавливают штатив с индикатором так чтобы его измерительный наконечник касался измерительной поверхности оправки и был направлен к ее оси перпендикулярно образующей. Итак нам необходимо обеспечить значительную величину тока с применением параллельно соединённых элементов питания.
Пока!
https://group.od.ua/67_zhiemchuzhina
120 mg prednisone – buy 10 mg prednisone prescription prednisone cost
Free Porn Galleries – Hot Sex Pictures
http://creedmoor.alexysexy.com/?monica
bollywood porn gay heroin porn movies sports porn tubes hunger games porn lily thai porn star getting fucked
Custom research paper ghostwriter for hire ca .
Proceed to Order!!! http://dryerzinia.com/index.php/User:Annajohnsonus
UYhjhgTDkJHVy
Drug prescribing information. Brand names.
buy valtrex no prescription in US
Actual news about drugs. Read now.
Компания ” Льняные Традиции” предлагает льняную ,смесовую и хлопкосодержащую ткань, а так же готовые изделия от основных производителей России по приемлемым ценам. Мы будем рады видеть Вас в числе наших клиентов. Рассмотрим любые предложения. Принимаем заказы на пошив.
Перейти на сайт
г.Иваново телефон: 8(920)676-97-56
Meds information for patients. What side effects?
generic valtrex without insurance in Canada
Some what you want to know about medicament. Get information here.
Pills information sheet. Cautions.
get valtrex online in Canada
All about medicament. Get now.
Pay for my ecology book review .
Proceed to Order!!! http://twitter.podnova.com/go/?url=https://essaypro.co
UYhjhgTDkJHVy
https://bonkers.name/
can you buy trazodone
cost cheap trazodone no prescription
https://nomitfinans.ru/
https://www.alltolearn.com/7tal77j/
Wonderful content. Thank you!
Hortense (Hortense) https://mru.org/user/178038/
Getting extra money has never been easier – simply copy the 1XBET Mongolia promocode , paste it in the appropriate section during registration, make a deposit and enjoy 1XBET Mongolia bonus. 1xbet promo code
My new hot project|enjoy new website
http://evansvillejanekershawporn.alypics.com/?allison
all star porn girls dutch porn tubes sahnel porn innocent girl porn tubes k9 porn tube
https://www.alltolearn.com/wgcrtgw/
your articles are very good and your blog site is really good
cheap trazodone prices
http://kinozapas.me/
Hello. And Bye.
http://csu-konda-mp4.ru/author/admin/page/51
Sexy teen photo galleries
http://tattoogirls.allproblog.com/?riley
female disney porn pakastani an indian fucking porn videos of 1950 s porn lindsey lohan porn video chatzy ten porn
https://adopt10plus.com/question/gibiz6i/
Hot galleries, thousands new daily.
http://qualityhotporn.mcbee.alypics.com/?reagan
young but legal porn porn secret kid porn title object object vanity porn actress uncensored japanese porn
https://adopt10plus.com/question/of8kx3w/
выездной квиз
provigil a stimulant – modafinil anxiety provigil a stimulant
Meds information leaflet. Drug Class.
can i get effexor prices in US
All about drug. Get information now.
Kaymme ensin artikkelissa kaikki ylla olevat asiat lyhyesti lapi, jonka jalkeen syvennymme niihin tarkemmin. Luettuasi taman taydellisen oppaan kasinoista ilman rekisteroitymista, tulet tietamaan naista nettikasinoista kaiken seka hieman enemmankin.
Verkkosivusto: nettikasinot ilman rekisteroitymista
Medicines information leaflet. What side effects?
cephalexin pill in the USA
All about drug. Read information here.
Drugs information sheet. Drug Class.
cheap erythromycin without insurance in US
Actual about medication. Get information here.
ASmartTV apparatus is just a television set with integrated Internet capacities and also perhaps a set top box for television, that supplies higher-level computing connectivity along with ability in comparison to thecontemporary standard television collection. SmartTV enables access such as graphics, screens, movie games, songs, apps, and a whole lot more.
Sexy photo galleries, daily updated collections
http://porn.av.movies.instakink.com/?julie
best on demand porn young girl eating pussy porn mom force porn videos ggg porn actresses tenio porn
Enjoy our scandal amateur galleries that looks incredibly dirty
http://gilbertsville.footjob.gigixo.com/?arely
free hot babe full porn videos classic golden porn jays porn office fitch porn site gay painter porn
Medicament information leaflet. Effects of Drug Abuse.
cheap cytotec prices in the USA
Best what you want to know about drugs. Get information here.
https://hollyclub.com.ua/
If your self will need toward crank out films toward write-up upon social media this sort of as Fb and Instagram or as your WhatsApp region, oneself can retain the services of windows xp sp3.
I love meeting people so contact me.
As dogs age, they can develop problems like arthritis, hip dysplasia, and other joint difficulties. To greatly help with those issues, a reassuring dog bed is crucial to cushion your dog’s human anatomy and supply rest from the pain related to celiac wellness problems. A comfy additionally encourages the joints of developing puppies too, making that a superior night’s break.
Hardcore Galleries with hot Hardcore photos
http://pornauntmom.relayblog.com/?izabella
adulteries porn mandy bright porn ass porn image gallery cocktails 5 clip porn tube cum filled boys free porn video
azithromycin – buy zithromax 100mg z pak antibiotics
42 years old Dressmaker or Tailor Donahey from Mount Albert, loves to spend some time reading to the, and scrabble. Continues to be inspired how big the earth is after visiting Flemish Béguinages
Scandal porn galleries, daily updated lists
http://vintage.porn.sexjanet.com/?bianca
porn movies online with piss scenes free frat party porn gay black thug porn download free safe porn websites dark mix porn mix
Critical analysis writers for hire usa .
Proceed to Order!!! http://sigha.tuna.be/exlink.php?url=https://www-cashnetusa-com-login.blogspot.com/
UYhjhgTDkJHVy
Dirty Porn Photos, daily updated galleries
http://sexmovieshemale.shemalebbmpin.energysexy.com/?cynthia
winona ryder porn free download videos porn blocked porn sites free porn piv search mature japanese mothers porn videos
Dirty Porn Photos, daily updated galleries
http://fewwpornvidslibby.moesexy.com/?mercedes
nude porn google video porn stars named pennie from texas veronicas porn pics ovidie porn free porn necrophiliac
What do you have to do?
Go through online registration!
Time for one service takes 10-20 minutes.
One evening = 300$
If you have access to a large number of people, the conditions can be individual! (Looking for partners)
You can find out more in the telegram:
@Verifed_in_eu_bot
Быстро и недорого. Разработка сайтов
Good day! Looking for a sponsor. My profile on the search site:
https://datingforkings.club/ My Name: Alisa Lozavarova
Hardcore Galleries with hot Hardcore photos
http://pretyputtyporn.kanakox.com/?izabella
cristina bella free porn pics kami andrews porn star 1 girl 2 boys porn movies free online sex porn erotic games heather deep throat tube 8 porn
Esl business plan editing websites for college .
Order NOW!!! https://getpocket.com/@pigeonviolet3
UYhjhgTDkJHVy
What can be better than this wonderful website and a cup of coffee in the evening!
נערות לבוי
Точное время, часовой пояс, разница во времени, время восхода и заката, основные факты о Москва, Россия.
Узнать время в Москве онлайн.
furosemide pills – lasix 2.5 mg where to buy lasix water pill
your articles and comments are really good. We wissh you success.
Hot new pictures each day
http://robinleeporn.fetlifeblog.com/?darby
animal porn online for free free teen porn threesome throat porn tube pics of mexican porn shemale schoolgirl porn
https://devki.su/
Professional term paper writers services au .
Proceed to Order!!! http://www.sensibleendowment.com/go.php/102/?url=https://essaypro.me/
UYhjhgTDkJHVy
http://pjjxw.com/home.php?mod=space&uid=45495
Привет полезный строительный портал
https://mnogovdom.ru/wp-login.php?action=lostpassword&redirect_to=https%3A%2F%2Fmnogovdom.ru%2Fprivacy-policy%2F
Sexy photo galleries, daily updated collections
http://freepornextermegeronimoestates.hotnatalia.com/?alanna
porn sport woman swimsuit free asian porn movie tube pichunter and nude and porn costume porn free movies twisted anal freaks porn
здраствуйте …
нашли с дочкой веб сайт нам нужно нанять C лазерная резка нашими задумками по ттеме
Просим C советом и как нам ,..
нузно знать как разобраться или быть в теме.,.
гибка металла москвапрошу c о вопросу будем сильнно благодарны .
огромное Спасибо =-) ,… нашел в instagremm @steelcentury пишите в ЛС Приветки много благодаренза ранее будем рады
https://skinali.photo-clip.ru/
Скидки на наполнителя для кошек и собак. корм для кошек
{north korea|kim jong un|trump china|seungri|terrorist attack|channel news
singapore news
Pills information sheet. Long-Term Effects.
order generic kamagra price in the USA
Best what you want to know about drug. Get now.
Esl definition essay writer website for school .
Order NOW!!! https://start01.ru/user/j9zljdc955
UYhjhgTDkJHVy
Приветки, сетевой народ!
Бросьте взгляд на интересный вебсайт
Идея вебресурса Нас спас удаленный бухгалтер. – Думается на должном уровне.
Всем пока, уважаемые господа.
Ефим
Sexy photo galleries, daily updated pics
http://shemaleporbn.allproblog.com/?alana
superhead vs mr marcus porn mothers sweet milk porn monson porn models free porn free porn comes home from war
Hot new pictures each day
http://reynoldsburg.wantedpornclips.topanasex.com/?madalyn
free preppy porn amature dog porn uk porn stars sites cele porn videos big omar tube porn
How to write a cv in .
Order NOW!!! http://google.com.bz/url?q=https://essaypro.co
UYhjhgTDkJHVy
Medicine prescribing information. What side effects?
buying generic tadacip tablets in USA
Best news about medication. Get information now.
Hardcore Galleries with hot Hardcore photos
http://old.young.porn.skippack.jsutandy.com/?nina
daily free porn stain video jungle voodoo porn porn poland innocent porn thumbs bedfordshire porn

100% free
make extra money at home as a freelanceer
作为自由èŒä¸šè€…在家赚å–é¢å¤–çš„é’±
à¤à¤• फà¥à¤°à¥€à¤²à¤¾à¤‚सर के रूप में घर पर अतिरिकà¥à¤¤ पैसा कमाà¤à¤‚
Gana dinero extra en casa como autónomo
كسب أموال إضاÙية ÙÙŠ المنزل
gagner de l’argent supplémentaire à la maison en tant que pigiste
зарабатывать дополнительные деньги дома как фриланÑер
New Freelancer Live streaming per hour service
UseFreelancer.com NEW live streaming software to get one on one per hour live service Such as Online teacher, Babysitting, Cooking Lessons, Craft Lessons, Fitness Lessons, Lawyer consultation, Doctor online visits, Coding Lessons, Language Lessons, any Lessons, Online Music Lessons, using our NEW lives streaming per hour service software, and you can have your own affiliates
for more details
https://www.usefreelancer.com
and start making money at home
Welcome to the new advanced UseFreelancer.com
Enjoy your time
Drug prescribing information. What side effects?
where can i buy eriacta in USA
All news about medication. Read here.
Medicines information for patients. Generic Name.
cheap eriacta without dr prescription in USA
Everything about medicament. Read now.
Hoвoe oнлaйн Kaзuно – Бoнyc кaждoмy!
Рeгистрирyйся – зaбери свoй Бoнyс и игрaй.
нeoграничeный дeпoзит, и мoмeнтльный вывoд!
https://cahopsong.tk/help/?15561621856649
Entry level resume no work experience .
Order NOW!!! https://ecosystem.fi/wiki/User:Annajohnsonus
UYhjhgTDkJHVy
buy clomid 50mg online – buy clomiphene 25mg clomid 50mg
https://greenshop.su/
New hot project galleries, daily updates
http://lesbianskatpornwomensbay.kanakox.com/?emilia
lebanease porn brazil porn july paiva panty porn pic best rough porn compilation lesbian strip porn
sildenafil 100 viagra ordonnance peut on acheter du viagra sans ordonnance
http://bit.do/fRvoF
https://devki.su/
10 good resume tips .
Proceed to Order!!! http://dryk.info/go?https://studybay.ws
UYhjhgTDkJHVy
sildenafil generique wrlviagra.com viagra generique
Trusted Online Casino Malaysia http://gm231.com/?s=#- Game Mania – GM231.COM – Click here>>>
Anonymous and the People’s Liberation Front are proud to announce a totally secure and safe alternative to the now infamous PasteBin service.
As many might be aware, PasteBin has been in the news lately for making some rather shady claims as to what they are willing to censor, and when they are willing to give up IP addresses to the authorities. And as a recent leak of private E-Mails show clearly, PasteBin is not only willing to give up IP addresses to governments – but apparently has already given many IPs to at least one private security firm. And these leaked E-Mail’s also revealed a distinct animosity towards Anonymous . And so the PLF and Anonymous have teamed up to offer a paste service truly free of all such nonsense. Here is a brief list of some of the features of AnonPaste.org:
No connection logs, period.
All pastes are encrypted BY THE BROWSER using 256 bit AES encryption. This means there is no usable paste data stored on the server for the authorities or anyone else to seize.
No moderation or censorship. Because the data on our servers is unreadable by us (or anyone), the responsibility for the legality or appropriateness of any paste lies solely with the person posting. So there will be no need for us to police this service, and in fact we don’t even have the ability of deleting any particular paste.
No advertisements. This service will be totally user supported through donations. Links for this are available on the web site.
Built in URL shortener for the convenience of people posting.
Paste services have become very popular, and many people want to post controversial material. This is especially so for those involved in Information Activism. We feel that it is essential that everyone, and especially those in the movement – have a safe and secure paste service that they can trust with their valuable and often politically sensitive material. As always, we believe in the radical notion that information should be free.
SIGNED — Anonymous and the Staff of the People’s Liberation Front PLF
https://anonpaste.org/
Free Porn Galleries – Hot Sex Pictures
http://cobalt.gigixo.com/?kari
porn pichunter lesbian porn with their numbers teens in college porn big tits teen porn tube kaykey porn
Looking for Good quality High authority Backlinks that help to grow Your Ranking ? You are in the right place. and i do offer you best and affordable SEO Backlinks Service , Thanks
You can Try My Service On Ebay here
Special Service available (increasing Ahrefs Domain Ratings Up to 50 plus)
https://www.ebay.com/usr/topseobacklinks
Sexy teen photo galleries
http://transsexmovies.hoterika.com/?brenda
fresh new porn free flics young blonde petite porn nigger porn 2009 jesloft enterprises ltd bisexual full length porn world biggest black dick porn tube
Sample argumentative essay pdf download .
Order NOW!!! http://ezproxy.lib.uh.edu/login?url=https://essaypro.me/
UYhjhgTDkJHVy
your blogs contain real information and you guys post great articles. we are grateful to you.
“I haven’t seen you in these parts,” the barkeep said, sidling settled to where I sat. “Repute’s Bao.” He stated it exuberantly, as if say of his exploits were shared by way of settlers around many a ‚lan in Aeternum.
He waved to a wooden butt beside us, and I returned his gesture with a nod. He filled a telescope and slid it to me across the stained red wood of the bar first continuing.
“As a betting man, I’d be assenting to wager a above-board speck of invent you’re in Ebonscale Reach for the purpose more than the carouse and sights,” he said, eyes glancing from the sword sheathed on my with it to the capitulate slung across my back.
http://maps.google.com.ec/url?q=https://renewworld.ru/new-world-kak-popast-na-alfa-i-beta-testy/
Casino bonusser er en rigtig god made for dig til at teste og afprove et online casino uden at lobe den store okonomiske risiko.
casino uden rofus
Заходи и выбери себе девочку! :0)
Самые горячие знакомства
Hot galleries, thousands new daily.
http://elbert.amandahot.com/?maya
porn star redd dawn bbw mature women free porn naruto and jiraiya porn free porn tube videos xnxx plumber nanny porn
Pingback: didier raoult hydroxychloroquine
Autobiography essay topics .
Order NOW!!! http://www.educacional.com.br/recursos/redirect.asp?url=https://telegra.ph/The-best-Side-of-essaypro-essay-writing-service-11-16
UYhjhgTDkJHVy
В сейчас огромную известность приобретают стеклокомпозитные комплектующие. Стеклокомпозиты состоят из 2 элементов: жидкой смолы и жесткой основы. Это дает изготавливаемым изделиям повышенную надежность.
Какие изделия изготавливаются из стеклопластиков?
– Емкости для химических жидкостей;
– Детали интерьера и экстерьера для автомобилей;
– Изделия для отдыха: парусные и моторные яхты.
http://www.find-a-teacher.org
Стеклокомпозиты в современном мире способны создать возможности для производственных отраслей. Весят много меньше железа и стали, дают похожие качества.
Если это сообщение попало не туда, очень вас просим отправить туда, куда нужно такие сообщения.
заказать рассылку по имейл
generic trazodone for sale
создание сайта цена
Создание сайтов Коломна
Molemmissa naissa on todella laaja pelikirjasto, joka sisaltaa tuhansia kolikkopeleja seka kattavan valikoiman kortti -ja poytapeleja. Molemmat tarjoavat myos mahdollisuuden kokea aitoa kivijalkakasinon tunnelmaa heidan live -jakajien hoitamassa Live -kasinossa.
brite nettikasinot
come dimagrire
Free christmas homework passes .
Order NOW!!! https://morphomics.science/wiki/The_Basic_Principles_Of_Buy_Dissertation
UYhjhgTDkJHVy
retail price of viagra – buy generic viagra without prescription best price for viagra in uk
hydroxychloroquine and lupus who hydroxychloroquine where can i buy plaquenil
come dimagrire velocemente
Sexy teen photo galleries
http://freegrannyporn.hotblognetwork.com/?kelli
island porn cartoons flash point porn porn tube contest porn pictures devon james free nylon hose porn
http://loveplanet.cf/
best way t o take viagra purchase viagra no prescription rgyqcts – buy viagra dublin
Type my human resource management dissertation methodology .
Proceed to Order!!! https://www.fcc.gov/fcc-bin/bye?https://essaypro.co/
UYhjhgTDkJHVy
Neurontin is used for treating seizures associated with epilepsy.
Buy cheap neurontin online and save your money. Only highest quality and secure payments. Free delivery and free pills for every order.
Only 0.58 usd per pill!
Минфин России не обсуждает и не рассматривает ни в каком виде введение налога на мясо, сообщила пресс-служба министерства.
Спецпредставитель президента РФ по вопросам цифрового и технологического развития Дмитрий Песков, выступая в среду на интенсиве “Архипелаг 2121” в Великом Новгороде, допустил вероятность введения налога на мясо как способа сдерживания климатических изменений.
“Введение налога на мясо в России не планируется. Минфин России не готовит подобного рода поправок в налоговое законодательство, этот вопрос в целом не обсуждается и не рассматривается ни в каком виде”, – говорится в сообщении.
Позднее Песков пояснил, что налог на мясо, который может стать инструментом учета углеродного следа в животноводстве, будет вводиться для стран-экспортеров, а не потребителей. Активное обсуждение этой темы в мире начнется после 2025 года, когда быстрый рост среднегодовой температуры на планете потребует пересмотра Парижского соглашения, считает эксперт.
Наши официальные партнеры – UGG Australia Москва
строительство домов под ключ
дизайн буклета заказать
Free Porn Pictures and Best HD Sex Photos
http://freepornarena.bastrop.sexjanet.com/?melina
daddy daughter porn free video cartoon charater porn talk dirty to me porn movie gothic porn free videos harrdcore porn movies jeans teen
Срочный ремонт ноутбуков в Москве на дому
reduslim opinioni amazon
can i purchase cialis over the counter – cialis for women buy tadalafil 20mg uk
как на xiaomi копировать контакты Как на Xiaomi перенести или копировать контакты с сим карты на телефон, с телефона на сим-карту, на аккаунт Google, Mi и другие варианты импорта и экспорта контактов.
reduslim quante compresse sono
Informa Mystery Shopping Login – secure
Resume for young college student .
Order NOW!!! https://victims.wiki/index.php/User:Studybayscom
UYhjhgTDkJHVy
dieta reduslim
Enjoy our scandal amateur galleries that looks incredibly dirty
http://puneshemale.amandahot.com/?ashleigh
porn women alphabetical order taking virginity porn free porn videos doggy style vanessa hudhens porn extreme pussy pounding porn vid
come dimagrire velocemente la pancia
perdere peso in 3 giorni
Hot new pictures each day
http://gayguidospornbellamy.hotnatalia.com/?janiya
momy loves cock porn real harry potter porn the best free porn movies websites jessica jaymes hd porn skooby doo costume porn
Интернет-магазин продает дизайнерскую мебель собственного производства по привлекательным ценам. В случае если не желаете покупать стандартные мебельные гарнитуры, а желаете выбрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы можете выбрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения изготавливается в разных стилях. Покупатели могут подобрать дизайнерские мебельные комплекты для комнат, выполненных в классическом, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Кроме столов, стульев, шкафов, консолей и прочей мебели на сайте фирмы «Эксив» вы можете выбрать дизайнерские предметы декора, которые дополнят интерьер и придадут помещению особенность. Зеркала, люстры, торшеры, бра, светильники можно найти для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://farming-mods.com/.
Предметы мебели изготавливаются из натуральных по максимуму материалов с качественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас изготавливается из массива дерева.
Как можно сделать заказа в онлайн-магазине бренда Exiv
В перечне вы сможете выбрать готовые изделия и заказать изготовление мебели нужной для вас конфигурации по личным размерам. При всем этом у вас будет возможность помимо этого найти цвет материала отделки.
Окончательная стоимость выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Для того чтобы узнать цену, позвоните менеджеру по телефонам, указанным на сайте. По заказу мебель изготавливается в среднем в течение 2-3 недель. Помимо этого можно забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в компании «Эксив» можно с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы России. Цена доставки по Москве – 1000 р. Для того чтобы узнать стоимость доставки в другие города, позвоните консультанту или задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными или банковской картой. Помимо этого можно оплатить товар на портале или по безналичному расчету. Если заказ отправляется в регионы, нужно полная предоплата.
болты и винты
come dimagrire drasticamente
ремонт холодильников на дому москва
reduslim composizione chimica
Let`s explore a world of Wild Fantasies. As Real As You Want it To be. Tonight only the hottest girls are waiting for you here
I solemnly swear that I’m up to no good
reduslim e ipotiroidismo
New super hot photo galleries, daily updated collections
http://townandcountrysarajayporn.alexysexy.com/?sydni
filipina porn thai bankok german porn movie reveiw girls ongirls free porn cheap porn on demand download porn to mp3 player
Cheap literature review ghostwriters site .
Proceed to Order!!! https://0rz.tw/create?url=https%3A%2F%2Fwww.folkd.com%2Fsubmit%2Fresearchpaper.edu.pl%2F
UYhjhgTDkJHVy
Интернет-магазин продает дизайнерскую мебель личного производства по привлекательным ценам. В случае если не желаете покупать стандартные мебельные гарнитуры, а желаете подобрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы сможете выбрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения изготавливается в различных стилях. Покупатели могут подобрать дизайнерские мебельные комплекты для комнат, выполненных в традиционном, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Помимо столов, стульев, шкафов, консолей и иной мебели на портале организации «Эксив» вы можете выбрать дизайнерские предметы декора, которые дополнят интерьер и придадут помещению особенность. Зеркала, люстры, торшеры, бра, светильники можно выбрать для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://farming-mods.com/.
Предметы мебели делаются из натуральных по максимуму материалов с качественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас делается из массива дерева.
Как сделать заказа в онлайн-магазине бренда Exiv
В перечне вы сможете выбрать готовые изделия и заказать изготовление мебели подходящей для вас конфигурации по личным размерам. При этом у вас будет возможность кроме этого выбрать цвет материала отделки.
Окончательная стоимость выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Для того чтобы уточнить цену, позвоните менеджеру по телефонам, указанным на веб-сайте. По заказу мебель делается в среднем в течение 2-3 недель. Помимо этого вы можете забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в компании «Эксив» можно с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы Рф. Стоимость доставки по Москве – 1000 р. Для того чтобы узнать стоимость доставки в другие города, позвоните консультанту либо задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными либо банковской картой. Помимо этого можно оплатить товар на портале или по безналичному расчету. Если заказ отправляется в регионы, требуется полная предоплата.
reduslim farmacia prezzo
perdere peso uomo
reduslim lo trovo in farmacia
reduslim opinioni mediche
dieta per perdere peso
Teen Girls Pussy Pics. Hot galleries
http://fortleonardwoodphoque.porn.danexxx.com/?aubrie
scarlett rouge porn free mobile indian porn porn capital of the us 3d comic porn gallery hot over 40 porn
https://www.infyseo.com/free-seo-audit-tool/en/domain/bitcoinforearnings.com
http://seoroast.com/domain/es.bitcoinforearnings.com
http://monitorawebsite.com/domain/de.bitcoinforearnings.com
lasix over the counter lasix generic name cheap lasix online
https://mutawakkil.com/domain/bitcoinforearnings.com
reduslim per dimagrire
http://sitevalue.epizy.com/show.php?url=https%3A%2F%2Fit.bitcoinforearnings.com
https://allseochecker.net/domain/de.bitcoinforearnings.com
I’m a simple girl who loves having fun chatting and meeting new people. You will always find me smiling and happy because nothing disturb me!
reduslim capsule
https://sitecurious.com/domain/de.bitcoinforearnings.com
Cheap phd papers assistance .
Order NOW!!! https://images.google.com.vn/url?q=https://edubirdie.review/
UYhjhgTDkJHVy
Sexy photo galleries, daily updated pics
http://holophonicporntuskegee.kanakox.com/?joslyn
miss milf porn free hairy porn online brazilian salsa porn dance free mother son porn free porn archives pics
congestive heart failure lasix furosemide is used for lisinopril and furosemide
https://www.5na5.ru/en/domain/es.bitcoinforearnings.com
Hi there. I’m often alone in my bedroom. I’ll fulfill all your disires. I can play so that we cum together! I love to hear about your fantasies. Let`s explore a world of Wild Fantasies. I like to learn new things. I enjoy showing off my curves and I dare you to make me bend…
I solemnly swear that I’m up to no good!
reduslim anche per uomo
ivermectin 3mg for lice – stromectol 3mg online stromectol for human
В московском аэропорту Шереметьево в субботу, 7 августа началась эвакуация пассажиров и персонала, сообщил Telegram-канал «Кухня Аэрофлота».
«Администрация сообщает, что из-за технических неполадок нужно покинуть аэропорт и отойти подальше», — написали администраторы канала.
При этом они отметили, что ни персонал, ни пассажиры на призывы эвакуироваться не отреагировали и продолжали оставаться в аэропорту.
Через несколько минут стало известно, что эвакуация закончилась. «Скорее всего, была учебная тревога», — отметил Telegram-канал.
В беседе с «Мослентой» сотрудники службы транспортной безопасности Шереметьево отказались прокомментировать ситуацию. «Мы не можем предоставить такую информацию», — сказали работники аэропорта. Позже стало известно, что в Шереметьево проводился тест системы оповещения.
Сейчас аэропорт работает в штатном режиме.
Ранее ребенок травмировал руку в одном из лифтов аэропорта Шереметьево. Московская межрегиональная транспортная прокуратура начала проверку.
Финансовые спонсоры – займ на карту онлайн
https://analysis.prc.digital/domain/es.bitcoinforearnings.com
reduslim funziona
https://runningseo.com/audit/domain/it.bitcoinforearnings.com
https://nibbler.silktide.com/en_US/reports/it.bitcoinforearnings.com
http://www.analayzer.seoxbusiness.com/domain/bitcoinforearnings.com
https://calidadweb.es/analizar-mi-web/en/domain/it.bitcoinforearnings.com
reduslim che cosa e
http://monitorawebsite.com/domain/es.bitcoinforearnings.com
https://reanimator.net/domain/de.bitcoinforearnings.com
Sexy teen photo galleries
http://attalla.rutoporn.alexysexy.com/?breonna
young men and mature women porn through the looking glass porn once more with feeling porn porn star cj cheat porn videos
alimentazione per perdere peso
Way cool! Some extremely valid points! I appreciate you writing this post plus https://is.gd/cqWEK4
reduslim altroconsumo
http://alonismarketing.com/domain/it.bitcoinforearnings.com
https://www.tripadvisor.in/Profile/cletusluke
https://seositeanalyze.com/domain/es.bitcoinforearnings.com
reduslim in farmacia prezzo
https://independent.academia.edu/LaquitaPoston?from_navbar=true
Cheap homework ghostwriters service .
Proceed to Order!!! https://maps.google.jo/url?q=https://studybays.com
UYhjhgTDkJHVy
https://nibbler.silktide.com/en_US/reports/de.bitcoinforearnings.com
https://www.ted.com/profiles/29584489
Hot photo galleries blogs and pictures
http://wendover.dildo.danexxx.com/?marlene
tex ex teen porn audrey porn mpeg dilevery man porn ray j porn sick fucking porn
шпильки
https://auditseo.eu/domain/it.bitcoinforearnings.com
https://soundcloud.com/user-522846548
http://de.bitcoinforearnings.com.sitescorechecker.com/
cos e reduslim
https://cafebabel.com/en/profile/alecia-rubin-610e4306f723b37b4b893fa1/
Best app ever…it really gives you real likes https://jpeg.ly/olEy
https://www.metal-archives.com/users/lashonclem
https://trustscam.fr/es.bitcoinforearnings.com
http://www.authorstream.com/aleciarubin/
https://www.analyzing.top/domain/bitcoinforearnings.com
effetti collaterali reduslim
https://www.analyzing.top/domain/es.bitcoinforearnings.com
https://www.ted.com/profiles/29584735
https://www.5na5.ru/en/domain/it.bitcoinforearnings.com
Sexy pictures each day
http://german.porn.hotnatalia.com/?allyssa
jessica sierra porn video free preview amature eastern teen porn animal porn vids sex and humour porn milf porn vidos
http://beristain.udeo.edu.gt/user/laquitaposton/
https://seo.liquidpurple.com/seo-turbo/domain/de.bitcoinforearnings.com/qkqH610e279bc3d4a
Girls of Desire: All babes in one place, crazy, art
http://flintpornstarttboy.hoterika.com/?karissa
cartoon porn movie archive christine young canada porn gay muscular porn porn art galleries free catoon porn tapes
https://www.tripadvisor.in/Profile/lashonclem
Hey, hope you are well! I’m a simple girl who loves having fun chatting and meeting new people. You will always find me smiling and happy because nothing disturb me!
I solemnly swear that I’m up to no good!
perdere peso camminando
https://www.askans.net/seo/en/domain/es.bitcoinforearnings.com
Sexy pictures each day
http://williams.amandahot.com/?adrienne
strange ugly tits porn tube goddes lexis porn video porn free long euro sleeping teen porn free pprn star three breasts
http://beristain.udeo.edu.gt/user/cletusluke/
Good warehouse objective for resume .
Order NOW!!! http://www.ccwin.cn/space-uid-4546107.html
UYhjhgTDkJHVy
hollywood casino online – real money casino app chumba casino
https://www.5na5.ru/en/domain/bitcoinforearnings.com
Your personal growth laboratory
Ежедневные траты не дают возможности накопить деньги? Хватит считать каждую копейку! Ты можешь зарабатывать, не выходя из дома! Подробности тут https://drive.google.com/file/d/12lv0auYW8lycilTsulkQYZf-u-1HLzmt/view?usp=sharing
reduslim bugiardino
http://qooh.me/cletusluke
https://seowave.org/en/domain/it.bitcoinforearnings.com/j5Un610e7b0e64549
https://trello.com/cletusluke
Sexy photo galleries, daily updated collections
http://old.young.porn.danexxx.com/?cristina
anna kornikova porn fat grannies sex porn tubes free porn young humorous extreme porn archives wild nasty porn videos
reduslim ebay
https://www.whoisua.com/en/domain/es.bitcoinforearnings.com
https://8tracks.com/aleciarubin
https://askzipy.com/tools/websiteanalyser/domain/bitcoinforearnings.com/TWGO610e07e3217c7
composizione di reduslim
https://homeinspectionforum.net/user/profile/40532.page
http://firsteverysearch.com/domain/de.bitcoinforearnings.com
https://www.scoop.it/u/laquita-poston
https://credibleaudit.com/domain/de.bitcoinforearnings.com
reduslim si trova in farmacia
https://erotag.org/
https://torgi.gov.ru/forum/user/profile/1480224.page
https://analytics.index.pe/en/domain/bitcoinforearnings.com
Free Porn Pictures and Best HD Sex Photos
http://la.tina.ranch.gay.porn.porn.jsutandy.com/?kiara
porn frequency for sky box porn seduction video porn free blowjob clips russian and porn freaky hardcore lrsbian free porn
http://www.edu.fudanedu.uk/user/cletusluke/
como perder peso rapido
шпонка
https://www.setlinks.ru/stat/?url=https%3A%2F%2Fbitcoinforearnings.com
https://letterboxd.com/lashonclem/
шпильки
https://orpho.ru/project.php?t=bftk4zku78zjgf6d
reduslim parere medico
https://seoanalyse.romtec.ch/en/domain/de.bitcoinforearnings.com/Bdu5610e2d3e22876
Thank you
https://homeinspectionforum.net/user/profile/40540.page
ingredienti reduslim
https://orpho.ru/project.php?t=yn2ldethsthhphnf
Hot teen pics
http://oakland.oldpornvideo.amandahot.com/?janae
home made porn movies mature clips jayne porn video how to block porn on computer porn videos to your inbox wapbu free porn video
Simple essay on pune city .
Proceed to Order!!! http://www.djps.chc.edu.tw/dyna/webs/gotourl.php?url=https://studybay.ws
UYhjhgTDkJHVy
https://weheartit.com/cletusluke
https://dobrapozycja.pl/en/domain/es.bitcoinforearnings.com/KXfC610e66b34449c
dimagrire, come dimagrire
http://www.cruzroja.es/creforumvolint_en/user/profile/175592.page
https://mutawakkil.com/domain
https://images.google.com.tn/url?q=https://lte-proxy.ru/
https://www.minds.com/aleciarubin/
reduslim blog
https://images.google.gp/url?q=https://lte-proxy.ru/
https://seo-kueche.partners/WebsiteReview/de/domain/it.bitcoinforearnings.com
https://torgi.gov.ru/forum/user/profile/1480202.page
https://turboseo.es/domain/it.bitcoinforearnings.com/XOfa610e80b3c2db9
Come perdere la pancia
https://pastebin.com/u/lashonclem
https://sitedd.com/en/domain/es.bitcoinforearnings.com
http://qooh.me/laquitaposton
reduslim prezzo piu basso
https://web-test.app/en/domain/de.bitcoinforearnings.com
https://disqus.com/by/aleciarubin/about/
>$50>
https://seowave.org/en/domain/bitcoinforearnings.com/xilK610e241ccb0fb
https://p-tweets.com/laquitaposton
reduslim cena
https://mijnwebsitescan.nl/check/verfication
I am addicted, it is happening instantly but my only question is it possible to choose your audience? eg country https://tinyurl.com/ygsmrrxa
http://maps.google.by/url?q=https://g-creative.ru/
Moje pary poszukują szczerego również indywidualnego zachowania, jakie doprowadza się mi obcowań nich mocno rzędu, a owym jedynym podeprzeć całe miłości z dzionka ożenku, zażyłe poruszenia spójniki zdjąć najmilszą rodzinę a wielbicieli. Które są moje mgły? Bojowi, nie boją się wyzwań zaś wiadomości. Przedkładają wykreować lekarstwo partykularnego, co uzmysławia Ich natura spójniki przymiot a przy tymże przyziemnie… będą sobą.
Utrwalić uwielbienie, beztroska, cześć, natomiast widocznie bystrość, kontakt, dobro – taka obligatoryjna funkcjonowań podobizna suknia, jaka nawet po latkach zajmuje, prosząc najstrojniejsze sekundy w trwaniu małżeństwa. Dokument ślubny egzystuje teraz gwoli sporo nowożeńców pamięcią, na którą specjalnie pragną po uczynionej loterii dodatkowo małżeńskim otrzymaniu. Zwolnienia baby przesądzają gwoli mężów niewypowiedzianą liczba, do której gęsto wspominają tudzież jaką owacyjnie płatają się z najprzyjaźniejszymi. Toż suma jest w wystawanie dostarczyć innym małżonkom Łukasz Popielarz – Fotograf Ślubny
Sesja ślubna w odbyciu to gracja wielce niż klawo dobrany krajobraz ślubny czyli praktycznie zestawiona Mgła Niedojrzała. Zaoszczędzenie przepaści, podkreślenie wzruszeń, natomiast przy współczesnym przystosowanie opraw do przymiotu niedorosłych partnerów – na owo wznoszę w mojej harówki. W fotografiach odnajdziecie przepisaną swojską przygodę. Teraźniejszą, która Was zjednoczyła dodatkowo jaką będziecie solidarnie pozostawać przed tamto dzionki rodowitego utrzymania. Poradzę Wam dopisać jej wybuch – Wasz ożenek – jaki spoi Was na ustawicznie jednorazowo oraz weselisko, które odczujemy razem spośród rodziną także sympatykami. Uchwycimy sekundy, do których będziecie marzyć zaś udowodnimy duże czułości, które będą Wam wtórować w teraźniejszym bezkonkurencyjnym klimacie. Przystań mi skomponować pamięć spośród najważniejszego dnia w Waszym bytowaniu !
czytaj wiecej fotografia ślubna
the best ed pill – ed pills cheap for him ed pills
Daily updated super sexy photo galleries
http://bestchinesefood.relayblog.com/?aubrey
little lupe free porn vids thai teen porn long amateur porn movies bound wedgie porn russian porn outside
http://maps.google.at/url?q=https://g-creative.ru/
Literature review writing websites .
Proceed to Order!!! http://www.bbs.91tata.com/home.php?mod=space&uid=5188155
UYhjhgTDkJHVy
Sexy photo galleries, daily updated collections
http://porntopayfor.tolu.amandahot.com/?mariah
ghana porn rihanna porn digg ridiculously free gay porn whipped ass porn porn star michael b
https://rusmuz.net/
https://seoaudit.app/domain/it.bitcoinforearnings.com
https://www.bitsdujour.com/profiles/ITgdLC
Star Stable kody są dostępne na wszystkich urządzeniach wyposażonych w Windows, Android lub iOS. Czity do Star Stable działa wykrywając Twój adres ip oraz powiązaną z nim nazwę użytkownika. Nasza platforma webowa jest bardzo przejrzysta i prosta w użyciu. Star Stable Hack jest niewykrywalny i działa na każdym istniejącym urządzeniu mobilny oraz stacjonarnym. Wystarczy wybrać nasze urządzenie z listy dostępnych i kliknąć generuj. Nie trzeba nic pobierać i instalować, kroki jakie musi wykonać gracz zostały ograniczone do absolutnego minimum. Wszystko odbywa się online.
Funkcje hack do Star Stable
Gra Star Stable jest cudowną ale jednocześnie prostą grą przeglądarkową wyprodukowaną przez studio Good Games. Grafika jest prosta i tradycyjna ale przykuwa uwagę gracza. Grę charakteryzują szybkie misje oraz zadania do wykonania. Star Stable jest darmowe ale wewnątrz gry można dokonywać zakupów za prawdziwą gotówkę. Można kupić monety, starcoins oraz star raiders coins. Tematem przewodnim gry są oczywiste wspaniałe zwierzęta jakimi są konie. Gra jest przeznaczona głównie dla młodszych graczy aczkolwiek każdy fan koni powinien znaleźć tutaj coś dla siebie. Oczywiście w grze da się wygrywać bez płacenia prawdziwymi pieniędzmi zdobywając powoli starcoins jednak jest to bardzo czasochłonne i męczące. Właśnie z myślą i niecierpliwych graczach powstał nasz Star Stable Cheats. Aby nasz stadnina robiła wrażenie warto z niego skorzystać i przyspieszyć budowę kolejnych atrakcji oraz ulepszeń. W grze jest mnóstwo ulepszeń oraz dodatkowych funkcji ułatwiających nam rozwój. Jedyne czego potrzeba do ich zakupienia są właśnie monety które możecie wygenerować za pomocą naszego hacka. Nasze kody do Star Stable są zupełnie darmowe, wystarczy przejść kilka kroków i generator zrobi swoje.
Przypominamy i podkreślamy jeszcze raz, że do użycia hacka nie potrzeba żadnej specjalistycznej wiedzy z zakresu programowania. Nasz aplikacja stworzona jest w taki sposób aby każdy bez instalacji programu i grzebania w bebechach swojego systemu mógł ją użyć. Generować surowce można codziennie, nic nie stoi na przeszkodzie aby to robić nawet częściej. Hack jest codziennie testowany i weryfikowany.
czytaj wiecej Star Stable darmowe Star coins
https://trustscam.es/de.bitcoinforearnings.com
Привет господа
Бурение скважин
В этой статье мы Вам расскажем для чего необходимо бурение и какие виды бурения бывают.
Для чего необходимо бурение скважины?
В загородных постройках, которые находятся на большом расстоянии от централизованных систем, остро встает вопрос персонального водоснабжения. Использование подземных источников позволяет вести автономное существование с максимальным и рациональным уровнем комфорта.
Помимо обеспечения водой, крайне необходимо чтобы вода была и пригодной к употреблению и использованию в домашних условиях. Подземные воды, изолированные толщами горных пород от поверхностного загрязнения, отвечают санитарным нормам, установленным для воды бытового назначения. При дополнительной очистке, проходя через фильтровальное устройство, они приобретают высокое качество. Для того чтобы получить доступ к источникам воды — требуется бурение скважин под воду.
Для определения способа бурения водозаборной скважины на участке нужно правильно определить глубину уровня подземных вод и породы геологического разреза, которые подлежат проходке. Правильно выбранная технология бурения скважин на воду позволит быстро пробурить скважину, избежать аварийных ситуаций при бурении. Наши специалисты выедут на участок и помогут определить вид и способ бурения, который будет оптимальным именно для вашего участка.
Бурение скважины
Бурение скважин — это способ и режим разрушения различных горных пород, очищение ствола скважины и укрепление ее стенок, оборудование водоприемной части.
В процессе бурения будет образовано направленное отверстие цилиндрической формы в породе, которое необходимо для монтажа обсадной колоны. Такая скважина представляет собой гидротехническое сооружение, имеющее круглое сечение, а глубина ее бурения зависит от особенностей грунта. Перед тем, как обустроить водозабор необходимо установить на какой глубине находится, водоносные слои и от этого будет зависеть способ бурения, которое бывает роторным и шнековым.
Виды бурения
Шнековое Бурение — это способ вращательного бурения при котором порода от забоя до верха скважины поднимается при помощи шнека — буровой трубы с наваренной на неё стальной лентой. На нижнем конце первого шнека установлен режущий наконечник, он при вращении разрыхляет почву и по шнеку порода поднимается от забоя до устья скважины. Шнековый способ применяется при бурении неглубоких скважин в песчаных и глинистых породах, а так же в породах средней твердости.
Стоимость такого бурения в нашей компании 55 рублей за метр погонный.
Роторное Бурение (Бурение с промывкой или продувкой). При таком способе бурения используется оборудования вращательного типа. Порода разрушается специальным инструментом долотом. В результате поступательно-вращательных движений, оборудование постепенно заглубляется, а почва из забоя выводится наружу глиняным раствором, водой или сжатым воздухом. Применяется для бурения как мягких, так и твёрдых пород на довольно большую глубину. Скважины, сделанные роторным способом имеют более продолжительный срок службы.
Роторное Бурение в нашей организации стоит 60 рублей за метр погонный.
Виталий и Евгений – специалисты по бурению!
Виталий и Евгений — специалисты по бурению!
Пробурили на двоих не одну сотню скважин с 2006 года! Имея огромный опыт за плечами наши сотрудники нацелены на бурение в максимально короткие сроки, минимизируя ошибки и оперативно решать возникшие трудности на пути к вашей воде! А благодаря собственному автопарку, буровых установок, большого и дружного коллектива мы можем предложить максимально интересные условия для сотрудничества!
Задать интересующие вопросы можно заполнив форму ниже или позвонить нам по телефону:
+375 (29) 186-45-03
Обещаем, Вы не пожалеете!
Hot galleries, daily updated collections
http://barstowsiouxcityporn.adablog69.com/?mariana
a mothers love porn tube born to pimp porn best offers for porn sites free big hugh tit porn arrancar porn
https://www.kuvilam.in/domain/it.bitcoinforearnings.com
Гранитная брусчатка считается одним из наиболее надежных стройматериалов для укладки аллей, дорог, тротуаров. В зависимости от месторождения камня, брусчатка имеет расцветку от светло-серого до черного, розоватого, в оранжевую и красную крапинку. А купить брусчатку можно по самым различным ценам, потому как стоимость может зависеть от способа обработки и оттенка материала. По сути есть возможность значительно сэкономить, если приобретать строительный материал без посредников, ведь любая гранитная брусчатка цена производителей будет ниже, нежели у любых продавцов.
http://pesok.salonkamnya.ru/m_5_3.html
доломит облицовка
https://www.scoop.it/u/alecia-rubin
https://www.seoload.ru/health_check/report/2723/it.bitcoinforearnings.com
Incredible update of captchas regignizing package “XRumer 19.0 + XEvil”:
Captcha recognition of Google (ReCaptcha-2 and ReCaptcha-3), Facebook, BitFinex, Hotmail, Mail.Ru, SolveMedia, Steam,
and more than 12000 another categories of captcha,
with highest precision (80..100%) and highest speed (100 img per second).
You can use XEvil 5.0 with any most popular SEO/SMM software: iMacros, XRumer, SERP Parser, GSA SER, RankerX, ZennoPoster, Scrapebox, Senuke, FaucetCollector and more than 100 of other programms.
Interested? There are a lot of demo videos about XEvil in YouTube.
Free XEvil Demo available.
Good luck!
P.S. A Huge Discount -30% for XEvil full version until 15 Jan is AVAILABLE! 🙂
XEvil Net
https://pastebin.com/u/cletusluke
Хватит переплачивать и ждать!
Купи Plastation 5 со скидкой 30% уже сегодня.
Не усусти свой шайнс – предложение ограничено.
Все приставки в наличии, большой вибор аксесуаров.
https://cutt.us/lUuaM
https://website.informer.com/de.bitcoinforearnings.com
https://disqus.com/by/cletusluke/about/
https://seoanalyzer.me/domain/bitcoinforearnings.com
Vp operations cover letter examples .
Proceed to Order!!! https://scientific-programs.science/wiki/EssayTyper_essaytypercom
UYhjhgTDkJHVy
https://data.world/laquitaposton
https://tools.navee.asia/domain/de.bitcoinforearnings.com
https://letterboxd.com/laquitaposton/
https://calidadweb.es/analizar-mi-web/en/domain/de.bitcoinforearnings.com
https://dribbble.com/laquitaposton/about
https://lernoweb.com/seocheck/en/domain/bitcoinforearnings.com
https://weheartit.com/lashonclem
https://analysis.toprankon.com/domain/de.bitcoinforearnings.com
Best Nude Playmates & Centerfolds, Beautiful galleries daily updates
http://lorain.old70porn.miyuhot.com/?elle
porn delray beach florida spanking porn free gallery naked night elf porn derrick taylor porn star pov porn forums
Forex momentum trading strategy. https://forex-stock-bitcoin-brokers.com/comparison-rating-reviews.html
https://www.crunchyroll.com/user/aleciarubin
20 mg of prednisone 5mg prednisone – prednisone without prescription medication
https://seonercia.com/domain/de.bitcoinforearnings.com
https://coolors.co/u/lashon_clem
Best Nude Playmates & Centerfolds, Beautiful galleries daily updates
http://pornmytube.instasexyblog.com/?tania
boys fucking animals porn my elmo girl porn mommie porn porn teenage pussy step daughther bathtub porn vids
https://www.google.tl/url?q=https://sarov.domabaninn.ru/
https://www.fooscan.com/domain/it.bitcoinforearnings.com
prednisone 2 mg – how to get prednisone without a prescription prednisone pak
https://images.google.sh/url?q=https://kstovo.domabaninn.ru/
https://kwebby.com/domain/bitcoinforearnings.com/EftX610e19d4a2501
https://cafebabel.com/en/profile/cletus-luke-610e3696f723b37b4d20c246/
https://allseochecker.net/domain/de.bitcoinforearnings.com
http://www.google.nr/url?q=https://klin.drova-rub.ru/
https://seo-kueche.partners/WebsiteReview/de/domain/es.bitcoinforearnings.com
mytek brooklyn dac wire labs cabling loudspeaker stereophile 07/19/2010
https://images.google.ad/url?q=https://dmitrov.drova-rub.ru/
https://www.mobypicture.com/user/lashonclem
John lewis gaddis thesis cold war .
Order NOW!!! http://maple.linppt.cc/home.php?mod=space&uid=1259473
UYhjhgTDkJHVy
https://www.pageranked.com/domain/de.bitcoinforearnings.com
http://maps.google.co.ug/url?q=https://ramenskoe.drova-rub.ru/
https://gotartwork.com/Profile/lashon-clem/102308/
https://grafx.co/about/
https://check.bel-web.com/en/domain/es.bitcoinforearnings.com
http://images.google.cn/url?q=https://lyubertsy.drova-rub.ru/
https://seo.data-minds.de/en/domain/de.bitcoinforearnings.com
https://coub.com/lashonclem
https://siteprice.com/
https://www.google.bi/url?q=https://serpuhov.drova-rub.ru/
Browse over 500 000 of the best porn galleries, daily updated collections
http://dating.women.xblognetwork.com/?mallory
big girl tiny girl porn free sleazy porn hot vietnamese french porn girl cyril cole porn brandy c free porn
https://registars.co/domain
https://milfsgame.com/tag/arab-niqab/
https://goldstick.ru/
http://classiccarsales.ie/author/laquitaposton/
https://google.rs/url?q=https://taldom.drova-rub.ru/
Daily updated super sexy photo galleries
http://edenton.casting.porn.sexjanet.com/?mariah
hot poop porn floating porn new free teen latina porn deep deep throat porn free porn trailers to watch
https://my-nm.store/
Отвечаю, если кто сомневался, вот Бот бесплатный фарм для Мафии Сити
https://web-test.app/en/domain/bitcoinforearnings.com
Girls of Desire: All babes in one place, crazy, art
http://jugsteenporn.lauderhill.hoterika.com/?brianne
stepdad licks young daughters cunt porn meagan fox porn video internet for porn wow sexy muscles porn free adult interactive porn
https://www.wishlistr.com/LaquitaPoston/
https://www.vizw.net/
https://www.bitrated.com/cletusluke
https://seoapp.es/en/domain/es.bitcoinforearnings.com
Girls of Desire: All babes in one place, crazy, art
http://westportsmouthpornstarlucien.amandahot.com/?janice
free teen tube porn video qaulity free porn peaches and eve porn all natural porn tube free iphone porn college
https://trustscam.de/bitcoinforearnings.com
https://google.mn/url?q=https://ivanteevka.drova-rub.ru/
https://www.crunchyroll.com/user/LaquitaPoston
http://analayzer.seoxbusiness.com/domain/it.bitcoinforearnings.com
https://google.sc/url?q=https://kashira.drova-rub.ru/
https://www.atlasobscura.com/users/laquitaposton
Esl dissertation conclusion ghostwriter site .
Order NOW!!! http://www.elymart.com/story.php?title=a-review-of-edubirdie-com
UYhjhgTDkJHVy
https://dnscheck.pingdom.com/#5ec7c08f9a000000
http://images.google.co.mz/url?q=https://protvino.drova-rub.ru/
Sexy photo galleries, daily updated collections
http://german.porn.kanakox.com/?kayleigh
mofosex boy porn video porn anal blow ebony and ivory free paris hilton porn clip porn pics in class porn movie clips rachel steele
https://maps.google.mg/url?q=https://ozery.drova-rub.ru/
https://w3seotools.com/seo-audit/de.bitcoinforearnings.com
https://images.google.com.bd/url?q=https://puschino.drova-rub.ru/
http://maps.google.tt/url?q=https://puschino.drova-rub.ru/
https://seo.liquidpurple.com/seo-turbo/domain/it.bitcoinforearnings.com/SdgG610e783f71a09
https://dribbble.com/lashonclem
https://www.crunchyroll.com/user/lashonclem
https://setiathome.berkeley.edu/show_user.php?userid=11063677
viagra 200 mg online – sildenafil mexico generic viagra without a prescription
http://fudanedu.uk/user/laquitaposton/
Sample business plan operating plan .
Proceed to Order!!! http://www.google.pl/url?q=https://essaypro.co
UYhjhgTDkJHVy
https://www.metal-archives.com/users/laquitaposton
Hot new pictures each day
http://brabiepornanselmo.hotnatalia.com/?mariela
porn classic forum free full amateur porn pure 18 porn bbaby sitter hot russian girls porn stream lusty porn
https://list.ly/aleciarubin/lists
Купить полиэтиленовые пакеты майка онлайн от производителя «Полимер» самые низкие цены, и супер быстрая доставка
https://trello.com/lashonclem
Mumbai alone now accounts for 25,500 COVID-19 cases including 882 deaths. Mumbai: Maharashtra registered as many as 2,345 new …
Mumbai
https://artmight.com/user/profile/224975
https://soundcloud.com/user-633598920
Enjoy our scandal amateur galleries that looks incredibly dirty
http://mount.sterling.sex.sexjanet.com/?keira
pics of student porn sex public creampie porn black and asian lesbian porn addiction porn signs of relapse gonzo porn movie
http://google.com.nf/url?q=https://zelenodolsk.drova-rub.ru/
My new hot project|enjoy new website
http://woodycreeksisterpornpics.danexxx.com/?bailey
littlest boys gay porn free movie download for adult porn watch black chicks pokrn isabella sky porn free celebrity blowjpb porn
https://pbase.com/laquitaposton/profile
https://my-nm.store/
https://google.rs/url?q=https://sterlitamak.drova-rub.ru/
http://v48100ec.bget.ru/user/Laquita+Poston/
https://list.ly/cletusluke/lists
https://jobgirl24.ru/
New super hot photo galleries, daily updated collections
http://worthington.springs.squirting.porn.topanasex.com/?annabella
full length adult porn videos free porn user uploaded julius caesar porn woman getting oral sex porn elesbian porn
https://www.ted.com/profiles/29582523
https://www.forexfactory.com/cletusluke
stromectol covid 19 best price on ivermectin pills – ivermectin tablets order
Хватит переплачивать и ждать!
Купи Plastation 5 со скидкой 30% уже сегодня.
Не усусти свой шайнс – предложение ограничено.
Все приставки в наличии, большой вибор аксесуаров.
https://is.gd/eC9AAu
https://www.4shared.com/u/-e9Q-YXz/cletusluke.html
Cheap application letter proofreading services for school .
Order NOW!!! https://easybookmark.win/story.php?title=5-simple-statements-about-payday-loans-online-explained#discuss
UYhjhgTDkJHVy
https://www.bitsdujour.com/profiles/qencmP
http://www.cruzroja.es/creforumvolint_en/user/profile/175578.page
https://www.pinterest.com.au/lashonclem/_saved/
https://en.eyeka.com/u/aleciarubin
https://soundcloud.com/user-929948110
Hot sexy porn projects, daily updates
http://kiron.cornyporntube.lexixxx.com/?priscila
warner brothers cartoon porn homemade young teen milf creampie porn core porn wemon squirting milf las vegas porn young toplist porn vid
Официальный сайт статистики coronavirus в Российской федерации – Coronavirus-Control.ru, разместил исследование от авторитетных экспертов и докторов о коронавирусе, со ссылками на государственные источники Johns Hopkins University – https://covid51.ru/ Эта информация для меня была ценна, сохранил в закладки.
https://weheartit.com/aleciarubin
Enjoy our scandal amateur galleries that looks incredibly dirty
http://strang.pornindiateen.miyuhot.com/?alina
one full length movie porn girl fucks in porn interview young teenage porn mobile videos free new porn chat mature porn tube net
https://artmight.com/user/profile/224916
Hot teen pics
http://aulanderitunespornapp.lexixxx.com/?jaylene
von brandis porn lesbian gigabyte porn video welch vineyard porn college spring break porn video japneese porn
https://www.mobypicture.com/user/aleciarubin
The posts and articles you share are very successful. congratulations.
https://www.forexfactory.com/lashonclem
Pingback: buy generic stromectol
cialis uk paypal – Cialis online usa tadalafil buy
Simple definition of a business plan .
Order NOW!!! http://akhmadiinkhotkhon-1.ub.gov.mn/?p=515
UYhjhgTDkJHVy
New project started to be available today, check it out
http://cutten.beach.sexjanet.com/?johanna
black free mobile porn man horse porn free classie porn free amateur wife submitted porn free big titties xxx porn videos
http://www.google.st/url?q=https://ussuriysk.drova-rub.ru/
http://google.co.il/url?q=https://surgut.drova-rub.ru/
https://www.goodreads.com/user/show/138640393-lashon-clem
https://images.google.us/url?q=https://kovrov.drova-rub.ru/
Приветствуем вас для сайте kozhainfo.ru!
Наш сайт посвящен всевозможным заболеваниям кожи. Здесь вы сможете найти исчерпывающую информацию по симптомам, причинам, методам лечения касательно вашей проблемы, а также встречать фотографии болезней и различные картинки упрощающие понимание сути болезни
https://pbase.com/lashonclem/profile
http://maps.google.com.pe/url?q=https://barnaul.drova-rub.ru/
College Girls Porn Pics
http://raretopporn.welch.hoterika.com/?daniela
winamp porn video porn retro tube small sex with fat women porn teagan pressley porn star free porn stories pe be
https://loading.express/?test_id=610e701f4af38c11144f8f9c&server=main
your comments and articles are really good
https://weblinkpedia.com/?noniID=siteinfo&url=https%3A%2F%2Fit.bitcoinforearnings.com
Cv musical resume .
Order NOW!!! https://www.indiegogo.com/individuals/25194424
UYhjhgTDkJHVy
http://www.google.com.hk/url?q=https://saratov.drova-rub.ru/
https://comodesenvolver.com.br/revisor-turbo/en/domain/bitcoinforearnings.com
http://www.google.com.hk/url?q=https://kamyshin.drova-rub.ru/
https://www.websiteworth.info/es.bitcoinforearnings.com.html
https://seo.analizsaita.online/en/domain/es.bitcoinforearnings.com
https://www.raskrutisam.com/en/domain/bitcoinforearnings.com
https://www.google.pn/url?q=https://kaluga.drova-rub.ru/
http://serp.heribertomacedo.com/domain/it.bitcoinforearnings.com
https://maps.google.kz/url?q=https://severodvinsk.drova-rub.ru/
http://www.analayzer.seoxbusiness.com/domain/it.bitcoinforearnings.com
https://premium-apartments.com.ua/
https://www.myseotool.net/domain/de.bitcoinforearnings.com
https://www.pageranked.com/domain/bitcoinforearnings.com
https://rusmuz.net/
https://mysiterank.org/en/domain/it.bitcoinforearnings.com
Enjoy daily galleries
http://schbigschick.instakink.com/?kamryn
torrets free porn animated animal sex porn dutch porn mags worlds largest porn video site vintage lesbian nun pron
https://sitechecker.pro/app/main/project/2239840/audit/summary?utm_campaign=redirecttest
https://trustscam.es/bitcoinforearnings.com
https://optimisu.com/domain/bitcoinforearnings.com
Победитель лотереи Saturday Lotto о себе и планах на жизнь:
Мы были убеждены, что наши участники — люди интересные и не примитивные!
Вот, к примеру, интервью одного из наших победителей. Максим Г. угадал все числа второй категории “5+S” и выиграл 8 736,07 USD (или 11 893,89 AUD австралийских долларов) в Австралийской лотерее Saturday Lotto.
Максим рассказал о себе и поделился планами на будущее:
— Расскажите о себе: Какая у Вас деятельность? Чем вы увлекаетесь, как проводите свободное время?
На Ваши вопросы отвечу без проблем. Мне 53 года, по профессии я механик судовых морозильных устройств. Много лет увлекаюсь игрой на гитаре. Обожаю слушать и играть блюз, люблю природу и пытаюсь по возможности непременно выехать на несколько дней из города.
— Что воодушевило Вас начать принимать участие в лотереях? Как Вы нашли наш сайт Agentlotto.Org?
Играть в лотереи я всегда любил и покупал систематически билеты на другом лотто сайте ***. Не знаю, почему там, как-то про него чаще видел информацию в сети.
Особых призов не было. На то, что выигрывал, сразу покупал билеты. Ситуация эта продолжалась до тех пор, пока я не решил потестировать Ваш сайт. Скажу честно, ранее изучал уже его, но не особо пристально! Совсем недавно решился изучить повнимательнее.
Причина, по которой я перешёл к вам, — возможность приобрести 1 билет любой лотереи (чего нет у ***), удобный интерфейс, все просто и понятно, также приемлемая ценовая политика на покупаемые билеты и быстрая техническая поддержка.
— Расскажите о максимальном выигрыше, который вам удалось выиграть: в какую лотерею, сколько Вы выиграли, как Вы отреагировали на победу?
Самый крупный выигрыш за все время произошел только с Вами, на Вашем сайте! И я думаю, что это не просто так…!!!
— Представьте, что Вы сорвали умопомрачительный Джекпот. На что Вы потратите главный приз? Расскажите немного о своих планах.
Если удастся сорвать Джекпот, значительную часть потрачу на помощь нуждающимся людям. Для себя же открою сеть небольших заведений, где будет звучать только живой блюз!
***
Мы поздравляем нашего замечательного победителя с выигрышем! Желаем ему дальнейших побед и осуществления мечты — ведь кто не любит хорошую музыку?
А сегодня мы предлагаем вам принять участие в лучшие иностранные игры вместе с нами!
Австралийская игра Saturday Lotto – Отличные шансы и недорогие ставки здесь!
Risk analysis in research proposal .
Order NOW!!! https://saveyoursite.win/story.php?title=ideas-to-help-you-get-through-school#discuss
UYhjhgTDkJHVy
http://www.primariepuglia.it/domain/bitcoinforearnings.com
stromectol oral – ivermectin nz covid and ivermectin
Free Porn Pictures and Best HD Sex Photos
http://finleyville.anal.alypics.com/?alina
homemade black people porn swinger fam porn flash porn horny wild chair free hot sexy porn pics porn vidio with jilly killy
http://iblueseo.site/en/domain/es.bitcoinforearnings.com
http://seo.gb-media.pl/domain/es.bitcoinforearnings.com
https://mutawakkil.com/domain/bitcoinforearnings.com
http://stuffgate.com/bitcoinforearnings.com
http://google.com.fj/url?q=https://kursk.drova-rub.ru/
College Girls Porn Pics
http://dvdpornsales.houghton.hoterika.com/?ashtyn
aged moms tube porn online porn sites great britain porn for free free porn no credet card argentina free porn
https://images.google.sh/url?q=https://dimitrovgrad.drova-rub.ru/
https://allseochecker.net/domain/bitcoinforearnings.com
http://google.mv/url?q=https://nazran.drova-rub.ru/
https://sitegur.com/it.bitcoinforearnings.com
https://images.google.dk/url?q=https://abakan.drova-rub.ru/
https://canwaz.com/
https://www.google.com.tr/url?q=https://penza.drova-rub.ru/
https://images.google.ci/url?q=https://ivanovo.drova-rub.ru/
Ищете, где купить тросы, буксировочный трос бурлак?
Компания Метизы – крупный поставщик трос швартов от лучших производителей на территории России.
Вся продукция сертифицирована и имеет необходимые маркировки.
+7(4862)25-54-37
https://seo-analyzer.softcrony.com/domain/it.bitcoinforearnings.com
http://google.kz/url?q=https://spb.drova-rub.ru/
Write a single declarative thesis sentence .
Order NOW!!! https://list.ly/ortegagodfrey234
UYhjhgTDkJHVy
https://images.google.co.hu/url?q=https://arzamas.drova-rub.ru/
https://sgap.info/domain/bitcoinforearnings.com
Browse over 500 000 of the best porn galleries, daily updated collections
http://fredericktown.milf.sex.energysexy.com/?tatum
fre porn mobile dump your porn old womam sex porn free soccor porn godzilla of porn
Hot photo galleries blogs and pictures
http://pornavarose.instasexyblog.com/?brandy
allison porn star catholic truth about porn free really old vintage porn films class of 3000 cartoon porn asian blow jobs porn
Scholarship for college students no essay .
Proceed to Order!!! https://bikorsan.net/taksi-fiyatlari/17130/smart-trick-studybay-essay-writing-service-nobody-discussing
UYhjhgTDkJHVy
https://podari-video.su/
http://maps.google.no/url?q=https//pest-expert.ru
Gurgaon is a city just southwest of New Delhi in northern India. It’s known as a financial and technology hub. The Kingdom of Dreams is a large complex for theatrical shows. Sheetala Mata Mandir is an orange-and-white-striped Hindu temple. The Vintage Camera Museum showcases cameras and prints spanning a century. West of the city, Sultanpur National Park is home to hundreds of bird species.
Gurugram
Gurgaon is a city just southwest of New Delhi in northern India. It’s known as a financial and technology hub. The Kingdom of Dreams is a large complex for theatrical shows. Sheetala Mata Mandir is an orange-and-white-striped Hindu temple. The Vintage Camera Museum showcases cameras and prints spanning a century. West of the city, Sultanpur National Park is home to hundreds of bird species.
cheap erectile dysfunction – ed pills that work best ed drugs
meilleur site achat cialis tadalafil mylan 5 mg viagra cialis levitra spedra
Duke essay questions analysis .
Proceed to Order!!! https://brickipedia.info/index.php/User:EduBirdiecom
UYhjhgTDkJHVy
Pingback: ivermectin online uk
acheter cialis sans ordonnance en pharmacie tadalafil pas cher otc cialis
Chennai, on the Bay of Bengal in eastern India, is the capital of the state of Tamil Nadu. The city is home to Fort St. George, built in 1644 and now a museum showcasing the city’s roots as a British military garrison and East India Company trading outpost, when it was called Madras. Religious sites include Kapaleeshwarar Temple, adorned with carved and painted gods, and St. Mary’s, a 17th-century Anglican church.
Chennai
Chennai, on the Bay of Bengal in eastern India, is the capital of the state of Tamil Nadu. The city is home to Fort St. George, built in 1644 and now a museum showcasing the city’s roots as a British military garrison and East India Company trading outpost, when it was called Madras. Religious sites include Kapaleeshwarar Temple, adorned with carved and painted gods, and St. Mary’s, a 17th-century Anglican church.
https://google.cf/url?q=https//pest-expert.ru
https://www.google.com.pk/url?q=https//dubna.pest-expert.ru
https://google.sc/url?q=https//domodedovo.pest-expert.ru
https://maps.google.ne/url?q=https//kotelniki.pest-expert.ru
Best curriculum vitae writers websites online .
Proceed to Order!!! http://ya4r.net/go.php?url=https://studybays.com
UYhjhgTDkJHVy
https://images.google.bs/url?q=https//krasnozavodsk.pest-expert.ru
yorkshire puppies for sale
Игровые автоматы Пин Ап Казино имеют официальную лицензию и стабильно выплачивают игрокам их выигрыши!
http://maps.google.com.ly/url?q=https//podolsk.pest-expert.ru
http://google.si/url?q=https//protvino.pest-expert.ru
ремонт холодильника москва
https://takiedela.ru/2019/06/teper-budem-igrat-v-bolnicu/
yorkie puppy for sale near me
Resume unix python new york education .
Order NOW!!! http://www.bbs.91tata.com/home.php?mod=space&uid=5041584
UYhjhgTDkJHVy
Дом Гуччи смотреть онлайн фильм
Однажды опробовав hydra сайт вам уже не захочется искать аналоги в подобной тематике. Интуитивно понятный интерфейс, система отзывов и техподдержки решает привычные проблемы покупателей.
hydraruzxpnew4af onion
https://stk-vrn.ru/
ivermectin children oral ivermectin generic ivermectin for horses
https://checkseosite.ru/ru/domain/bitcoinforearnings.com
Resume writing tips education .
Order NOW!!! http://forum.raceofman.dk/member.php?action=profile&uid=110336
UYhjhgTDkJHVy
Читы для любую игру покупать или приобрести безвозмездно можно для нашем самом быстрорастущем форуме читов и разных модов на самые популярные зрелище, но можно найти беспричинно же на редкие жанры игр. Услуга идти на крутой форум игрового шмота и других полезных фитчей.
https://yougame.biz/forums/34/
https://www.websitestatchecker.com/domain/bitcoinforearnings.com
Адвокат в Москве
https://comodesenvolver.com.br/revisor-turbo/en/domain/de.bitcoinforearnings.com
https://saunapeterburg.ru/
https://sitechecker.pro/app/main/traffic-checker-land?pageUrl=https:%2F%2Fes.bitcoinforearnings.com
Girls of Desire: All babes in one place, crazy, art
http://hugecockgayporn.juncal.miyuhot.com/?meadow
free mobile old young porn videos spy tube porn free teen lesbian finger porn sex porn best porn articles
Book report fill in sheet print .
Order NOW!!! https://gamesbanca.com/forum/profile.php?section=personality&id=587212
UYhjhgTDkJHVy
otc ivermectin ivermectin price ivermectin 100ml
https://analizador-web.tutorialesenlinea.es/domain/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
come perdere peso
Ремонт фундамента Красноярск
hydroxychloroquine eye exam plaquenil price plaquenil interactions with other drugs
come perdere la pancia
Ремонт фундамента Красноярск
Ремонт фундамента Красноярск
velocemente 10 kg in una settimana
Doctor is an idealistic inscription that originates from the Latin word of the unchanged spelling and meaning.] The word is at an agentive noun of the Latin verb docere ?ke?r?] ‘to guide’. It has been used as an visionary title in Europe since the 13th century, when the pre-eminent doctorates were awarded at the University of Bologna and the University of Paris.
Having happen to established in European universities, this usage spread everywhere the world. Contracted “Dr” or “Dr.”, it is used as a designation for a person who has obtained a doctorate (e.g., PhD). In assorted parts of the life it is also utilized by medical practitioners, regardless of whether they convoke a doctoral-level degree.
Ремонт фундамента Красноярск
perdere 10 kg in una settimana
в хорошем качестве смотреть фильмы онлайн бесплатно
reduslim
Why is homework good for students .
Proceed to Order!!! https://www.sharjahclassifieds.com/user/profile/28892
UYhjhgTDkJHVy
Ремонт фундамента Красноярск
College Girls Porn Pics
http://weirdfetish.bestsexyblog.com/?kiara
homemade porn send porn hub professional mature videos korean celebritie porn porn site with instant messaging free femalebodybuilding porn stars
dimagrire in fretta
Ремонт фундамента Красноярск
заказать логотип
Ремонт фундамента Красноярск
https://images.google.com.eg/url?q=https//schyolkovo.pest-expert.ru
albuterol sulfate – Albuterol online ventolin cost uk
продвижение в Вк
Ремонт фундамента Красноярск
Drugs prescribing information. Cautions.
meclizine online in Canada
All news about medicines. Read now.
https://images.google.ro/url?q=https//tuchkovo.pest-expert.ru
https://avtolombard-voronezh.ru/
Best mba personal essay help .
Order NOW!!! https://cse.google.com.ly/url?q=https://studybay.ws
UYhjhgTDkJHVy
https://www.askans.net/seo/en/domain/bitcoinforearnings.com
https://bitcoinforearnings.com.sitescorechecker.com/
reduslim gocce prezzo
Rodneytaibe
Ремонт фундамента Красноярск
Ремонт фундамента Красноярск
http://www.magnamultimedia.de/domain/de.bitcoinforearnings.com
http://maps.google.com.ec/url?q=https//novocherkassk.pest-expert.ru
http://analyzer.naijagodigital.com/domain/de.bitcoinforearnings.com/Tfrk610e3130394a1
Having turn established in European universities, this habit spread around the world. Contracted “Dr” or “Dr.”, it is tolerant of as a designation in place of a yourself who has obtained a doctorate (e.g., PhD). In various parts of the era it is also used aside medical practitioners, regardless of whether they hold a doctoral-level degree.
https://gitlab.pagedmedia.org/niecestorm71
Dirty Porn Photos, daily updated galleries
http://tiedcostumeporn.amandahot.com/?madisen
mom daugther porn free porn sites k9 celebrity porn hardcore incredbles porn 100 free flash tube porn
https://freeseofix.com/domain/bitcoinforearnings.com
https://seonizm.com/seo-checker/en/domain/de.bitcoinforearnings.com
Ремонт фундамента Красноярск
https://sauni-moskva.ru/
https://seo-optimierung.avalist.ch/check/verfication
A debutant actor Jay and his co-star Tara, an established actress, and a diva, decline in love on the sets of their film. Come what may, Tara is set to league David, a area potentate and a bureaucrat who is also the in of the movie. Twenty years later, Jay is a big big big shot but is calm in angel with Tara and decides to travel to Lisbon to apologize to her for something he did in the past. In the end, Jay finds that he has a daughter with Tara and that she has been also living a dual lifetime with her husband pining during the course of Jay.
https://coub.com/lovesoccer43
https://www.digitalfootprint.fi/domain
Ремонт фундамента Красноярск
https://www.seovue.com/analyzer/
роблокс пчеловод
Bee Swarm Simulator
Би Сварм
Bee Swarm
#yEv0kB
Ремонт фундамента Красноярск
https://seo.allmediacreation.ro/en/warning/restricted-words
http://www.stepbynet.com/domain/de.bitcoinforearnings.com
Race and your community research paper .
Order NOW!!! https://ccm.net/profile/user/endflame99
UYhjhgTDkJHVy
What’s up, its nice paragraph concerning media print, we all be aware of media is a
fantastic source of data.
https://serpch.com/audit/en/domain/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
Born in Beirut and raised in Toronto, Reeves began acting in histrionics productions and in boob tube films before making his best haze launch in Youngblood (1986). He had his breakthrough character in the body of laws fiction comedy Invoice & Ted’s Great Dare (1989), and he later reprised his job in its sequels. He gained praise for playing a hustler in the independent drama My Own Private Idaho (1991), and established himself as an action hero with pre-eminent roles in Stage Announce (1991) and Speed (1994).
http://sc.devb.gov.hk/TuniS/la-cocaine.org/
https://google.to/url?q=https//zaraysk.pest-expert.ru
Ремонт фундамента Красноярск
reduslim prezzo farmacia
Rodneytaibe
New super hot photo galleries, daily updated collections
http://88by88.pornmissionhill.alexysexy.com/?karly
japan porn vine attack teen titans porn clip free porn women like oshkosh wisconsin porn shop gail ye porn
http://smartseotools.site/domain/it.bitcoinforearnings.com
https://analysis.toprankon.com/domain/it.bitcoinforearnings.com
Доброго времени суток.
Подскажите хорошую типографию для изготовления буклетов
Могу посоветовать одну типографию , качество, цена и скорость у них отличное,
но они размещаются в Красноярске, а мне хотелось бы в Питере.
Это печать открыток https://4uprint.ru/products/otkrytki-priglashenija
Ремонт фундамента Красноярск
https://www.seo.gooktec.com/en/domain/it.bitcoinforearnings.com
https://google.com.mt/url?q=https//nevinnomyssk.pest-expert.ru
https://www.openadmintools.com/en/de.bitcoinforearnings.com/
Создание сайтов Москва
https://maps.google.jo/url?q=https//hasavyurt.pest-expert.ru
Мой стрим по игре Симулятор пчеловода !
Bee Swarm Simulator
БиСварм
Bee Roblox
Bee Swarm
tamoxifen bodybuilding nolvadex only pct tamoxifen pros and cons
Ремонт фундамента Красноярск
https://weblinkpedia.com/?noniID=siteinfo&url=https%3A%2F%2Fbitcoinforearnings.com
https://allseochecker.net/domain/bitcoinforearnings.com
Cheap persuasive essay writers for hire .
Proceed to Order!!! http://www.yyd157.cn/upload3/home.php?mod=space&uid=42639
UYhjhgTDkJHVy
http://www.analayzer.seoxbusiness.com/domain/bitcoinforearnings.com
https://www.google.bs/url?q=https//ussuriysk.pest-expert.ru
cytotec 200mg tablet – cytotec price in india cytotec online usa
prednisolone prednisone prednisolone cats prednisone chest tightness
Ремонт фундамента Красноярск
perdere peso velocemente
http://tools.avetis.co/domain/de.bitcoinforearnings.com
https://images.google.mv/url?q=https//pervouralsk.pest-expert.ru
https://kreditvesta.ru/
Мой стрим по игре Bee Swarm Simulator !
Би Сварм Симулятор
Би Сварм Симулятор
Симулятор Пчеловода
Bee Swarm
https://www.report.nadvertex.com/domain/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
Ремонт фундамента Красноярск
http://netfoxdigital.com/analyze/domain/es.bitcoinforearnings.com
perdere peso in una settimana
sms onay
Мой стрим по игре Bee Swarm Simulator !
Bee Swarm Simulator
Би Сварм
Би Сварм Симулятор
БиСварм
http://925millionaires.com/seo-analyzer/domain/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
ссылка гидра тор 6 – hidra com официальный, ссылка гидры
https://seo.ibumu.com/en/domain/it.bitcoinforearnings.com
It’s amazing to visit this web site and reading the views of all colleagues on the topic of this paragraph, while I am also keen of getting familiarity.
Blog writing research papers .
Order NOW!!! https://www.bookmark-fuel.win/the-biggest-problem-with-studubay-and-how-you-can-fix-it
UYhjhgTDkJHVy
http://google.com.ar/url?q=https//kemerovo.pest-expert.ru
Ремонт фундамента Красноярск
https://checkseosite.com/domain/de.bitcoinforearnings.com
Ремонт фундамента Красноярск
http://maps.google.com.gi/url?q=https//rubcovsk.pest-expert.ru
https://seoreport.leadwd.com/en/domain/es.bitcoinforearnings.com
Por ansiedad de rendimiento en el caso de disfunción eréctil se entiende como la presión psicológica para “rendir” adecuadamente durante el sexo. En estos casos, la ayuda temprana de un profesional puede ser determinante. http://www.igees.org/members/timothyamola/activity/442/
http://www.ludosln.net/analyse-seo/domain/it.bitcoinforearnings.com
https://www.5na5.ru/en/domain/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
https://orpho.ru/project.php?t=62c275cqnxapiwgv
https://steamauthenticator.com/
Если вы планируете поступление в чешский университет, перед вами обязательно будет стоять вопрос – Нострификации аттестата в Чехии. Чтобы пройти эту процедуру быстро и гарантированно, рекомендуем обратиться к профессионалам, которые работают в области нострификации в Чехии с 2010 года.
Нострификация аттестата
https://www.google.gp/url?q=https//arhangelsk.pest-expert.ru
Professional cover letter for principals .
Proceed to Order!!! http://www.huibangqyh.cn/home.php?mod=space&uid=80017
UYhjhgTDkJHVy
https://www.imkartikpandya.com/KPSEOTool/domain/de.bitcoinforearnings.com
https://maps.google.co.mz/url?q=https//ehngels.pest-expert.ru
https://www.trendupseo.com/domain/de.bitcoinforearnings.com
Ремонт фундамента Красноярск
https://reviewmywebsite.xyz/hi/domain/casinoonline.lt
CoinEx – International Cryptocurrency Exchange https://bit.ly/birgatut
#coinex #coinexcom
Best thesis proposal writing site for mba .
Proceed to Order!!! https://hernandoeducationfoundation.org/forums/users/annajohnsonus/
UYhjhgTDkJHVy
https://seomon.com/domain/bitcoinforearnings.com/
https://seodron.com/en/domain/it.bitcoinforearnings.com
https://nibbler.silktide.com/en_US/reports/es.bitcoinforearnings.com
Ремонт фундамента Красноярск
where to buy doxycycline in singapore – how to order doxycycline buy doxycycline over the counter uk
The pigman book report .
Proceed to Order!!! http://zagovorygadania.ru/user/studybayscom/
UYhjhgTDkJHVy
https://www.google.rw/url?q=https//rybinsk.pest-expert.ru
https://www.seocheck.io/en/domain/bitcoinforearnings.com
https://images.google.cv/url?q=https//lipeck.pest-expert.ru
https://seopop.xyz/domain/it.bitcoinforearnings.com
Доставка алкоголя якутск
https://www.atlasinstallers.com/author/etvtc/
https://www.fooscan.com/domain/de.bitcoinforearnings.com
Professional cover letter proofreading website online .
Order NOW!!! https://menwiki.men/wiki/The_smart_Trick_of_essaypro_That_Nobody_is_Discussing
UYhjhgTDkJHVy
https://sitefactum.net/domain/bitcoinforearnings.com
https://steamauthenticator.com/
https://check.bel-web.com/en/domain/bitcoinforearnings.com
güvenilir hizmet arayan kişiler sitemize giriş yaparak işlemlerini güveniir şekilde yapabilirler
https://google.am/url?q=https//saransk.pest-expert.ru
I read this article completely about the difference of most up-to-date and earlier technologies, it’s remarkable article.
https://google.to/url?q=https//astrahan.pest-expert.ru
Ремонт фундамента Красноярск
Custom dissertation ghostwriter services for college .
Proceed to Order!!! https://maps.google.com.gt/url?q=https://edubirdie.company
UYhjhgTDkJHVy
https://007.ae/domain/es.bitcoinforearnings.com
Доставка алкоголя якутск
https://www.google.as/url?q=https//zelenogorsk.pest-expert.ru
http://seobin.org/en/domain/es.bitcoinforearnings.com
Lucknow, a large city in northern India, is the capital of the state of Uttar Pradesh. Toward its center is Rumi Darwaza, a Mughal gateway. Nearby, the 18th-century Bara Imambara shrine has a huge arched hall. Upstairs, Bhool Bhulaiya is a maze of narrow tunnels with city views from its upper balconies. Close by, the grand Victorian Husainabad Clock Tower was built as a victory column in 1881.
https://www.techradar.com/reviews/remo-recover-review – Lucknow
Lucknow, a large city in northern India, is the capital of the state of Uttar Pradesh. Toward its center is Rumi Darwaza, a Mughal gateway. Nearby, the 18th-century Bara Imambara shrine has a huge arched hall. Upstairs, Bhool Bhulaiya is a maze of narrow tunnels with city views from its upper balconies. Close by, the grand Victorian Husainabad Clock Tower was built as a victory column in 1881.
http://maps.google.com.ly/url?q=https//oryol.pest-expert.ru
Доставка алкоголя якутск
Good day! This is kind of off topic but I need some guidance from an established blog.
Is it very hard to set up your own blog? I’m not very techincal but
I can figure things out pretty fast. I’m thinking about
making my own but I’m not sure where to begin. Do you have
any points or suggestions? With thanks
Jodhpur is a city in the Thar Desert of the northwest Indian state of Rajasthan. Its 15th-century Mehrangarh Fort is a former palace that’s now a museum, displaying weapons, paintings and elaborate royal palanquins (sedan chairs). Set on on a rocky outcrop, the fort overlooks the walled city, where many buildings are painted the city’s iconic shade of blue.
http://zip-repair-pro—repair-zip-files.sharewarejunction.com/ – Jodhpur
Jodhpur is a city in the Thar Desert of the northwest Indian state of Rajasthan. Its 15th-century Mehrangarh Fort is a former palace that’s now a museum, displaying weapons, paintings and elaborate royal palanquins (sedan chairs). Set on on a rocky outcrop, the fort overlooks the walled city, where many buildings are painted the city’s iconic shade of blue.
Ремонт фундамента Красноярск
https://nibbler.silktide.com/en_US/reports/bitcoinforearnings.com
сайт гидры на торе – гидра через тор, правильный адрес гидры
Доставка алкоголя якутск
https://www.google.at/url?q=https//gadchina.pest-expert.ru
You really make it seem so easy with your presentation but I find this topic to
be really something which I think I would never understand.
It seems too complex and very broad for me. I am looking forward for your next
post, I will try to get the hang of it!
http://www.google.com.ai/url?q=https//repino.pest-expert.ru
http://www.magnamultimedia.de/domain/it.bitcoinforearnings.com
https://images.google.com.ly/url?q=https://dzerzhinsk.domabaninn.ru/
Varanasi is a city in the northern Indian state of Uttar Pradesh dating to the 11th century B.C. Regarded as the spiritual capital of India, the city draws Hindu pilgrims who bathe in the Ganges River’s sacred waters and perform funeral rites. Along the city’s winding streets are some 2,000 temples, including Kashi Vishwanath, the “Golden Temple,” dedicated to the Hindu god Shiva.
https://freetuts.net/thu-thuat/phan-mem-khoi-phuc-du-lieu-tot-nhat-913t.html – Varanasi
Varanasi is a city in the northern Indian state of Uttar Pradesh dating to the 11th century B.C. Regarded as the spiritual capital of India, the city draws Hindu pilgrims who bathe in the Ganges River’s sacred waters and perform funeral rites. Along the city’s winding streets are some 2,000 temples, including Kashi Vishwanath, the “Golden Temple,” dedicated to the Hindu god Shiva.
Name research paper .
Proceed to Order!!! http://mohandestan.com/question/index.php?qa=32458&qa_1=edubirdie-com-writing-services-reviews
UYhjhgTDkJHVy
https://www.naverex.net/ru/node
http://images.google.com.qa/url?q=https://gorodets.domabaninn.ru/
trazodone pred forte
https://www.turbowebsite.ovh/domain/bitcoinforearnings.com
Доставка алкоголя якутск
Ремонт фундамента Красноярск
https://www.google.co.ao/url?q=https://navashino.domabaninn.ru/
https://images.google.gr/url?q=https://uren.domabaninn.ru/
https://bitcoinforearnings.com.statscrop.com/
https://list.ly/cletusluke/lists
https://seowebsiteanalyze.com/domain/it.bitcoinforearnings.com
https://bit.ly/3zi0Y05
reduslim su amazon
Rodneytaibe
neurontin rx – how much is neurontin pills levothyroxine 1 mg
http://seo.code95.info/domain/de.bitcoinforearnings.com
http://hotel-chatter.com/user/laquitaposton/
https://www.seoauditreporter.com/domain/es.bitcoinforearnings.com
Bulabilirim sitemiz ile aradığını bütün herşeyi hızlı şekilde bulabilirsiniz.
Ремонт фундамента Красноярск
http://vietnam-times.ru/press-release/osobennosti-kachestvennogo-remonta-kvartir/
Professional creative writing ghostwriting sites for masters .
Proceed to Order!!! https://vimeo.com/essaytyper
UYhjhgTDkJHVy
tamoxifen after menopause does tamoxifen cause bone loss tamoxifen gel
velocemente 10 kg in una settimana
prednisolone oral suspension for cats dogs prednisone dog prednisone dose
http://avtodom48.ru/kak-legalno-nanyat-rabochih-inostrantsev-dlya-remonta-kvartiryi
come dimagrire velocemente
недвижимость на северном кипре у моря
Professional term paper ghostwriter website uk .
Order NOW!!! https://shorl.com/pustosturihova
UYhjhgTDkJHVy
come dimagrire
Ремонт фундамента Красноярск
Читы в CS: GO — данное воспрещённые проекты какие предоставляют существенное превосходство во забаве Counter-Strike: Global Offensive. Из-За применение несовременных читов во 2020 вам сможете являться забанены VAC. В ezcheats вам сможете загрузить читы в КС спорт безвозмездно, в отсутствии микробов, хайдов также регистрации.
Значимость топика обозначает то что чит функционирует в заключительной версии Steam CS: GO также никак не найден античитом VAC (undetected).
https://ezcheats.ru/chity-cs-go/
Продвижение сайтов Москва
https://images.google.cv/url?q=https://spas-evacuator.ru/
Hardcore Galleries with hot Hardcore photos
http://hotpeoplepornrepton.miaxxx.com/?alana
free mobile porn no membership younget porn star ever hamster porn black cock rough best athletic porn sites black men white womn porn vos
северный кипр недвижимость распродажа
http://maps.google.com.pe/url?q=https://spas-evacuator.ru/
reduslim
GAGI.ru воры, кидающие на деньги
заманивают низкой ценой и на второй день отключают сервера без причины
деньи возвращать отказываются
Кидалы, не выдают сервера по несколько дней после оплаты и не возвращают обратно деньги.
Не связывайтесь ни в коем случае, если не хотите быть кинутым.
подробнее на zennolabe
купить квартиру на северном кипре
Hair styling in Kazan
Cheap expository essay ghostwriter service online .
Order NOW!!! https://godotengine.org/qa/index.php?qa=user&qa_1=divingwinter1
UYhjhgTDkJHVy
Pingback: dapoxetine tablets us
Хвaтит пeреплaчивaть и ждaть!
Кyпи Plastation 5 со cкидкoй 30% yже сeгодня.
Не упyсти cвой шaйнс – прeдлoжение oграничeно.
Все пристaвки в нaличии, бoльшой выбoр aкceсуаров.
https://is.gd/3UrwFb
северный кипр недвижимость
perdere peso velocemente
https://sms-service-online.com/en/receive-free-sms-Ukraine/
Hello, I enjoy reading through your article.
I wanted to write a little comment to support you.
недвижимость на северном кипре
perdere 10 kg in una settimana
Несколько дней назад осматривал материалы сети, и к своему восторгу заметил важный ресурс. Это он: https://sms-service-online.com/ru/temp-Phone-Numbers-for-WhatsApp/ . Для моих близких этот сайт явился довольно важным. Успехов всем!
вторичная недвижимость северного кипра
Viagra
bookmarked!!, I love your blog!
Here is my web-site – buy instagram views
(Ina)
Just desire to say your article is as astonishing.
The clearness in your publish is simply nice
and i could suppose you are a professional in this subject.
Fine along with your permission allow me to grasp your feed to stay up to date with approaching
post. Thank you 1,000,000 and please continue the enjoyable
work.
Stop by my web-site; Personal Computer
Attractive section of content. I just stumbled
upon your website and in accession capital to assert that I get
in fact enjoyed account your blog posts. Anyway I’ll be subscribing
to your feeds and even I achievement you access consistently fast.
my web blog … desktop computer – Cleo,
Hi, i read your blog occasionally and i own a similar one and i
was just wondering if you get a lot of spam comments?
If so how do you prevent it, any plugin or anything you can recommend?
I get so much lately it’s driving me mad so any support is very much appreciated.
Here is my webpage: gb whatsapp, Graig,
Poetry writers services .
Order NOW!!! https://telegra.ph/5-Easy-Facts-About-Research-Paper-Described-05-05
UYhjhgTDkJHVy
Wonderful goods from you, man. I’ve understand your stuff previous to and you’re just extremely fantastic.
I really like what you’ve acquired here, certainly like what you’re stating and the way
in which you say it. You make it entertaining and you
still care for to keep it smart. I can not wait to read much more from you.
This is actually a wonderful website.
Also visit my website whatsapp gb [Gregg]
May I just say what a comfort to uncover a person that truly knows what they’re
discussing on the web. You actually realize how to bring a problem to light and make it important.
More and more people ought to check this out and
understand this side of the story. I was surprised you are not more
popular given that you most certainly have the gift.
Feel free to surf to my blog post … cell phones (Latia)
Asking questions are truly good thing if you are not understanding something entirely, however this piece of writing offers fastidious understanding yet.
Here is my homepage; blogging (Emory)
perdere peso in una settimana
https://sms-service-online.com/en/temp-Phone-Numbers-for-Amazon/
недорогая недвижимость северного кипра
viagra price – viagra 200mg price
Почти час серфил контент сети, и вдруг к своему удивлению обнаружил лучший ресурс. Вот гляньте: https://sms-service-online.com/ru/temp-Phone-Numbers-for-craigslist/ . Для моих близких данный вебсайт оказался весьма привлекательным. Пока!
https://sms-service-online.com/en/temp-Phone-Numbers-for-instagram/
Professional ghostwriting service us .
Order NOW!!! http://forum.ateel.org/index.php?action=profile;area=forumprofile;u=407152
UYhjhgTDkJHVy
ремонт стиральных машин на дому
Прошлым вечером разглядывал содержание интернет, при этом к своему восторгу заметил нужный вебсайт. Вот ссылка: https://sms-service-online.com/ru/temp-Phone-Numbers-for-skype/ . Для моих близких этот веб-сайт произвел незабываемое впечатление. До свидания!
https://saunapeterburg.ru/
Superhighway Safety: Safe use of the Internet is a free pack published by the Department
for Education and Becta, covering issues such as acceptable use policies and setting up school websites.
It also advises on filtering systems, internet monitoring organisations and intellectual property and copyright.
Although there’s no such thing as completely free cam shows (webcam girls want to buy
iPhones and dress fancy, you know!), there’s a good share of XXX sites where you can take advantage of freemium offers implying zero fees in certain cases.
It can allow you to make better decisions and leave you feeling greater peace of mind.
Teen Chat Rooms Online Free Without Registration, Teen Chat Room live for girls and boys under age
13, 14, 15, 16, 17, 18, and, 19 to make new friends.
Whether you’re a first time visitor or a chat room veteran, we look forward to getting to know you.
Essay on sanskrit in sanskrit .
Order NOW!!! https://mogensencarne.livejournal.com/profile
UYhjhgTDkJHVy
Enjoy daily galleries
http://panfullporn.ivesdale.topanasex.com/?janiya
candy barr porn movie bug ass white girls porn moviesw best home porn porn film nero familiare the major gay porn studios
Rendering a realistic human is a process which historically required the specialized technical knowledge of
teams of artists in game and special effects studios. Some software that’s already available automates much of the process for creating the 3D likenesses of real
people. Others, not so much. Users can then use those 3D models to create still images and animated videos, or have sex with them using a VR headset and a connected sex toy like the Fleshlight Launch, which automatically strokes the person’s penis in sync with action on screen. You’ll still need to be
logged into Steam to view the list, but it’s a must-follow for smut aficionados who want to fill their Steam library with porn. But those laws vary by state,
and for ordinary individuals who don’t have a famous face, there
may be little legal recourse. You may just not be their
type. John Danaher, a senior lecturer in law at the National University of Ireland Galway and coeditor of the book Robot Sex:
Social and Ethical Implications, told Motherboard that
images and representations like this could be viewed as a type of revenge porn if they’re
created or shared without consent.
https://avtolombard-voronezh.ru/
fandom jamaac Ya que con aldu y cande lo hicimos podríamos juntar
los fandoms para que así mas gente se una! hagamos un Omegle entre todos los fandoms de lxs chicxs de
jamac! Vamos a entrar a Omegle, sin camara,>cha>,
con la palabra “jamac” para encontrarnos todos, den rt>
In the forthcoming paragraphs, we are going to enlighten you about the benefits that these websites offer you.
I contacted HP’s customer support line, but since the warranty has expired for nearly 4 years they
didn’t offer any support, not even letting me purchase
the battery and replace it myself. I originally looked on HP’s site as they list replacement parts for their
devices, but the battery was the only component that wasn’t available to purchase.
I know the laptop is 5 years old, but that is not an unreasonable amount of time to
keep replacement batteries, especially if they have
a backlog of every other component. The thing that has me running to you fine people is I have been looking at several sites trying to get the best price I
can and most are no longer selling the rtx2060 and tell
me they are being discontinued and they wont be stocking
them anymore meaning i can downgrade or pay more
for the rtx2070 which to be honest i would struggle to afford.
Since its a gaming laptop it wasn’t great when it was new, averaging around 5.5 to 6 hours, but now it can’t make a full hour without
being plugged into the wall.
bro you think famous dex hot so to you it’s not lol
@SmilesofSally I knew I detected an accent this
morning a little Tuscon I’m Genovese my mother and grandmother spoke Italian in the kitchen when we
were growing up all the time I thought I’d send this to you
here and not out to on Twitter or chattrubate
pornvi caughtcheatingporn jetsonsporn free1080pporn realteenporn freeonlineporn kitchenporn navajoporn dirtytalkingporn sleepoverporn kattleyaporn interactiveporngames lilyraderporn straightgayporn blackmalepornstars pornmagazine
clownpo…
https://buysildenshop.com/ – viagra 50 mg
should i eat these hot cheetos
Hello. And Bye.
We now have Rent-To-Own Adult Video Chat Turnkey Packages …
>adultvideochatsoftwar>
>adultvideochatbusines>
акустический поролон
my sex chatroom how to get breast naturally bigger movies having nudity sex cam sites
The defense attempted to portray Ravi as a tolerant person who showed bad judgment,
but not as someone who was biased against gay men and women. I think you’re making the right decision, and I wish you a lot of luck in finding
a psychiatrist who doesn’t routinely bark at you.
We are making sure that you are getting the very best of everything.
Our images are so true that you even can confuse the facts and
them. We have a ton of great hardcore content including
hot naked girls getting massive black cocks, amazing bukkake and cream pie scenes, and we even have scenes featuring MILFs, Cougars, GILFs,
and even young girls with horny old men. This is based on minute substances
called neuro-peptides that are apparently produced by
many tissues all over the body, including the brain, heart, immune system, digestive system, and blood cells.
• Go online: Online shopping has its own advantages which are applicable.
güvenilir hizmet arayan kişiler sitemize giriş yaparak işlemlerini güveniir şekilde yapabilirler
Dialogue in essays format .
Proceed to Order!!! http://www.russtars.tv/user/essaytyper-com/
UYhjhgTDkJHVy
Anywhere anytime 24 hours a day 7 days a week! Non stop!
70 girls, 9 studios, 35 cams, 7 days, 24 hours!
Welcome to Girls of Oz Cam Girls International Phone TV, a
Live Show, and Interactive Phone Show of the hottest
Cam Girls, Phone Babes, Glamour Models, and Porn Stars available in the world.
At Girls of Oz Cam Girls, we have Thousands of Horny Babes to choose from.
Then be sure to check on the thousands of other babes who are
live online direct from their own bedrooms. Then thanks to Girls
of Oz International Lives’ unique and convenient billing system.
Please note that not Phone Billing is only permitted in certain countries and carriers.
Private shows and credits can now be paid for either
by credit card or billed directly to your monthly phone bill.
There are Cam 2 Cam services, as well as two-way audio and remote control sex toy cam shows.
Ms. Proper then you must concentrate your Online Dating Community look
for to people internet dating services who have a sizable member’s program.
Then become a member of our adult webcam community and enjoy meeting and interacting with all the sexy couples on this page as well as watching all their free sex shows on our live cams!
All sort of girls come to our adult webcam site looking
for a good time. We specialize in live streaming web cams of the most beautiful teenage
girls getting frisky over the internet, be it as a solo performer,
lesbians, or couples. It’s littered with far too many short clips cutting out the
best stuff pushed out by the studios, and finding a good, high quality scene is getting more
and more difficult. Camming Is Very Popular Lately And One Of
The Best Ways To Masturbate Online. I decided to interview a cam girl name Ona Artist
who is essentially a camming celebrity—she has 1.3 million followers
on Instagram—to find out what that life is like.
Whether it’s girls going solo, lesbians, gays, couples, swingers, mature babes, trannies, you name it, we’ve got it right
here. “One of my participants had a particularly graphic show uploaded to a porn site, and it got a huge amount of views,” she
continues.
You’ve seen my shoes and clothing collection .
Don’t worry I’ve got your present sorted >xx>
Эти фильмы формировали сознание и мировосприятие миллионов людей, становясь неотъемлемой частью их жизни. смотреть СССР кино в интернете Не одно поколение выросло на классических советских кинолентах. Их любят, смотрят, цитируют и по сей день.
ucuz takipçi satın al işlemi yapmak istiyorsanız hemen sitemizi ziyaret ederek en güvenilir ödeme yöntemleri ile ucuz takipçi alabilirsiniz.
Salobre?a Salobre?a is a town full of charming whitewashed houses around a
typical small square at the top of the hill, which is the old Moorish fortress.
Petite with small natural breasts Ginebra Bellucci is
a cutie from Cordoba in Spain and is another that
has been very active in the short time she has been in the adult industry.
Is it normal for a rapist to show concern for their victims even several months after the incident?
The short answer to that is NO. He is not showing concern. Maybe it was simply the fact that I lost so much over
the past two weeks and this fugly black mask was really all I
had to show for it, but either way I kind of wanted to keep it.
Her bf had been begging her to capture the blowjob on film and
she finally agreed, now its all over the internet for everyone to see.
AntonyARLewis: @filmhana Agreed, the attention given has to be equal.
MikeGarley: @filmhana Making them cry was intentional. MikeGarley: @filmhana Yes, luckily it was intentional.
Wow! Theres an official Omegle iPhone app! You can waste so
many hours on that site, and its only going to be worse now!
I was thinking about this at 3:00a! “Sex work” another big umbrella that lets pimps and cam girls speak over trafficking victims and women who
want out.
Now the gaetz boy is a fortune teller? LOL! Guess what, gaetz?
The crimes have already stuck to the criminal, all the way back to paying off porn stars, sexually assaulting or raping women, & preventing a free
& fair election in 2016!
Watching all these girls suffer from violent men & sex trafficking makes me wanna so sad
generic cialis soft tab – buy generic cialis canadian pharmacy bluechew tadalafil
A very HappyThanksgiving to all my dear American friends xxx
Thanksgiving2019
online gay chat sites gay leuven free mens underwear giant penis porn
Better yet – do ‘nude>’ in watercolor or Polaroid or olg>home vidg>.
If it’s electronic, it’s out thep>
Ms Murphy wants people to realize and appreciate how much makeup the
porn stars are wearing, so that women, and men, don’t have unrealistic ‘ideals’
of how one should look. A lot of men are competing with women, and that’s very strange and unusual to me.
Maybelline Superstay 24 lip color is also a must, as are false eyelashes and the egg-shaped makeup sponge,
Beauty Blender. After starting her career at a makeup counter
in a Boston mall, Ms Murphy has been transforming porn stars
for eight years. I showed up and didn’t know that it was makeup and hair.
Above is the cover of the NY Post from March 29, 2014.
If you live outside of New York you may not
know that there was a tragic explosion here a few days ago.
To cover up adult movie performers’ blotchy skin, oily foreheads,
and pale complexions, she uses Make Up For Ever HD Invisible Cover foundation and concealer, according to the Huffington Post.
Her first job in the adult film business came when she began dog-walking duties for a porn director’s assistant, and was asked to transform
‘The Luscious Pornstar’ Gianna Michaels. Wild teens who want a good anal fucking for the first time, and busty milfs who want to squeeze
a boner between their generous boobs are all waiting
for you on the number one sextube.
This shit day is finally over. I’m going to relax in a good bath.
What are you doing on the way back? freeonlineporn pornotube
TRX19
HE WAS A TRUMP CAMPAIGN ADVISOR AND WHO HAS BEEN TO THE WHITE HOUSE TO VISIT WITH
TRUMP A BUNCH OF TIMES. HE WAS ALSO IN THE SEYCHELLES RIGHT AFTER THE ELECTION
IN 2016. HE WAS INDICTED ON CHILD SEX PORN CHARGES A FEW MONTHS AGO AND THEN AGAIN JUST RECENTLY, THE BEST PEOPLE SMDH
Let’s not forget male porn stars may not get paid as much but the top guys do about 300 paid
scenes a year & on average career last 7 years.
They are more also more likely to get directing jobs too.
How many female porn stars even shooting 100 paid scenes a year?
Then by following these 3 top methods to turn a profit through the best traffic building practices,
you actually will be able to increase the
income that you like through your Online business concern. He’d
realised he needed to know more about prostheses
before he could really make his own, so he convinced
FabTech – the company his prosthetist worked with – to hire
him part time, building devices. Even today, some amputees prefer the Dorrance hook over
all the fancy electronic devices out there. In 1912, an amputee named David Dorrance invented what’s
called the split-hook hand attachment for artificial arms – the first
that allowed users to grasp objects comfortably. The first time I met Brian in person was in Breckenridge,
Colorado. Canfield is himself an athlete; he bikes up and down mountains all
around Colorado. While Brian tried to make fine adjustments to the
knee, rotating the cams on the outside that control how tightly
the tendons pull, Canfield wasn’t listening.
Ulrika has been honest about he lack of intimacy
in her marriage and admitted she acquired blunt recommendation from her pals
on the matter. Ulrika mentioned her confidence was knocked by her lack of will or want to have intercourse, as well as putting on a small amount of weight and bodily indicators of ageing.
Explaining how she decided to just go for it in the bedroom,
she stated: ‘Weirdly with age comes all of the insecurities about my physique and ageing and all that stuff, however there also got here this superb sense of freedom.
There was no huge, dramatic farewell with Picasso.
Lydia claims that as a 19-yr-outdated Picasso appeared like a granddad or
father determine. Stop texting the guys you like! They’re the sweetest guys ever, everrrrr for the first few weeks or months relying on how long it takes for them to decide
they “have you”! The former Celebrity Big Brother star candidly admitted she thought she would by
no means have intercourse once more solely two years ago and
was frightened she wouldn’t remember the right way to have intercourse before she received right down to the deed.
Gay dating questions
Telegram-канал. Реклама в Pinterest дает Заказчикам из Etsy, amazon заработки от 7000 до 100 000 usd в месяц. https://t.me/pintetsy Ручная работа, Цена 300 – 500 usd за месяц
Is it possible to increase the size of your penis?
There are many ways to go about this journey and one of
the most popular and easy to do is a brief massaging during any of
the other penis enlargement exercise routines.
Just as you increase the size and girth of your
penis through stretching and massaging exercises so will you increase the size of your penis head.
Girth issues are some of the biggest sexual relationship topics these days
as many women even swear by the fact that they
wouldn’t care if their husbands and boyfriends were 4 inches long
as long as they were 4 inches wide! Revealing truth questions on sexy topics and sizzling hot dares
will keep your next party interesting. Once you have one, just keep tightening and releasing your anal muscles repeatedly until
you feel a bit of a burn in that particular area.
微信:aliceteas
正åb>, 學çb>, 嫩æb>, data-query-source=”hashtag_click” class=”twitter-hashtag pretty-link js-nav” data-query-source=”hashtag_click” class=”twitter-hashtag pretty-link js-nav”
savethechildren
Police: German chat groups trade child sex abuse …
free live pron ebony webcam porn skinny women with big boobs clothes for big bust
instagram takipçi satın al
Essay topics for the novel speak .
Proceed to Order!!! https://google.ch/url?q=https://studybay.ws
UYhjhgTDkJHVy
Let’s not forget male porn stars may not get paid as much but the top guys do about 300 paid scenes
a year & on average career last 7 years. They are more also more likely to
get directing jobs too.
How many female porn stars even shooting 100 paid scenes a year?
prednisolone ac side effects alternative to prednisone does prednisone make you gain weight
ebony webcam porn skinny women with big boobs clothes for big bust free live pron
does lasix cause gout lasix for swelling lasix retard
http://buytadalafshop.com/ – Cialis
Ucl history department essay guidelines .
Order NOW!!! https://bankersoil1.webgarden.cz/rubriky/bankersoil1-s-blog/new-step-by-step-map-for
UYhjhgTDkJHVy
instagram takipçi satın al
The tablet has a processor speed of seven hundred and twenty MHz while it has an internal memory of two hundred and fifty six MB.
I remember we were eating and small talking for a while when she was
finally like: so what is this opportunity you were talking about?
“I was born in Pennsylvania and grew up in a small town. Stranger Chat : Maybe the weirdest of all video webcam sites was the stranger chat sites. They work like chat roulette sites but stranger chat cam sites glorify the fact your talking on cam to strangers. Hidden cams a bit creepy in my opinion but most if not all these reallifecam sites are in fact just businesses trying to separate people from their money. Real Life Cams : Just as they sound, these types of webcam video chat sites typically cost money but enable users to peer into people’s lives in real time via voyeur cams. In modern society, real communication has been imperceptibly replaced by virtual communication. What’s more, you can even access cam chat rooms online for free.
We have recently added many new features, such as private chat, webcam search, sex
filter, hd quality video, and more! Close-up shaved pussy teen on webcam My little shaved pussy – Teen Webcam, Webcam Porn Plump shaved pussy lips
on webcam. Payments are regularly made twice per month, but it’s possible for models to request daily payout for an additional fee of $3.95.
Welcome to the Live Cams Mansion, home of the most beautiful
cam models in the world! Ever wonder what the girls do when they’re not on cam?
For only 25 credits a day OR FREE for VIP members, you can unlock our 24×7 LIVE spy cam feeds and take a peek into their everyday lives
in the mansion! As a registered voyeur member, there is no limit
to the amount of time you spend with any cam model performer.
Tip Anonymously: Sending your tip anonymously
will hide your identity from other users
in the chat room but the performer will still know that you sent the tip.
It is not my proof, that’s why America is so great,
1a free press! “lawyer Michael Cohen pleaded guilty to
eight federal charges on Tuesday, including campaign finance violations related to hush money payments he
made to porn actress Stormy Daniels during the 2016 election.”
Sex is genetic, male and female. Women are female, men are male.
Nobody with male DNA is a female, or vice versa.
Sex is not variable, changeable, or optional.
Copy as well as save a few of these great bios right into
a text document, after which you can examine them till you know very well
what tends to make them more effective. That way, you know it’s just going to be simpler.
Because, the Corrupt Ones WILLING OR NOT HAVE SIDED WITH THEIR FRIENDS, and they are also child abductors, child-sex-traders,
etc., and in being this way, they support millions of
other perverts on black markets, worldwide. We all have loads of erogenous
areas, find what works for your girl. Take a close look in this article you will find an outstanding article marketing tip that will
increase clickthroughs substantially to your sites. Display marketing ads are a primary tool
to grab customer eyeballs on travel blogging sites ultimately converting them on the brand’s website.
Digital Marketing allows brands to reach the right customer at
the right time and device.
0% porn
0% naked girls
0% gold chains
0% gangster criminals
0% poppin’ bottles
0% useless bling bling
100% real pure good music
Word? I only heard of navy federal
You’ll have the opportunity to chat with live sexy teen cams while you beat
your meat. YouTube while watching that video.
We’re sure that you’re going to find all the answers that you’re looking
for with us and we’re going to make sure that you have a proper time watching these cam girls
cause that’s the only thing that you deserve, only the best.
Our cam models will be there from the beginning of your erection until climax
and afterglow as well. It will take just one cam to cam sex
session and you’re going to be hooked, we guarantee it!
Get ready for some of the best mature women’s as they show you what a real cam performance
is. You can rest assured that she’s enjoying it just as much as you are, and you’ll get
to have a very intimate and interactive experience
with her. How Much Does This Cost?
Slut naked cam Miss_Julia: Damn right,i`m baaack!Ready to ride and get my freak on!Let`s get into those sexy pleasurable conversations and experience anything our minds desire!Make sure to ask for a DISCOUNT or better yet,join my FAN CLUB… hot>video cha>
However, a 2016 review of existing scientific literature on hormonal birth control and mood pointed out there
is a lack of research in this area, and that negative mood effects are measured differently in every study.
This applies even when clothing and accessories are meant to present women to men in an even more sexual light than they might otherwise appear.
The Terrapins scored the next four points, but Nebraska got even closer
with a 12-2 run that made it 56-54 at 7:37 on Green’s layup in transition. The
Terrapins (20-4, 10-3) won their seventh straight game,
went to 14-0 at home, and reached 20 wins for the fifth time in the past six
seasons. Web session has gotten a standard and WINS acknowledgment.
We are working hard to be the best Emo Pics site on the web!
One of the biggest and most complete JAV gravure sites on the web.
Dex…we were doing so good. I promised to not politics at
your funeral…you opened up about the Mandalorian…
Then you go and post this white hot garbage opinion. Why
you gotta be this way
WHY DO YOU PUSH ME AWAY LIKE THIS!
I hear Bing is the best search engine for porn. What’s your side hustle?
After all, we are all people and many who arrive “fresh” in London, might
find the big city atmosphere difficult to cope with when they first arrive.
You do actually get a lot of escorts from Barcelona working in London, and
the majority of them supply a very good service.
She started to work for a London escorts agency in North London a
few years ago, but is now working for a leading escorts agency in central London.
Since I started to date Brixton escorts, I have sort of got into adult comics.
At the same time, I started to appreciate that the porn industry is very profitable.
Of course, there are many other kinds of porn as well. They do not only offer
English but they often German and French
as well. The agency that I used was called Barcelona Angels,
and I swear that the girl I spoke to on the front desk was
Scottish but she insisted that she was Barcelona born and
bred, but her English teacher had been Scottish.
When he was twelve, he was arrested for punching a sixty-year-old female teacher who had caught him using drugs in the boy’s rest
room at school, breaking her jaw and leaving her with a concussion.
It is a general impression that paid online dating sites are safe and credible and assured of
privacy where as the free ones are not. Further,
certain parole violators are just not worth sending back to jail.
This style of diadem dates back to Alexander the Great, according
to a University of Chicago website on her beauty. This University of Chicago website
includes pictures, including busts showing her in the diadem.
Your wife can refrain from including herself in potentially compromising situations.
Assisted reproductive technology (ART), including In Vitro
Fertilization (IVF), requires procedures in which, eggs from female and sperms from the male
are combined outside the body. It doesn’t matter if you are hetro,
gay, bi, or anything else. After reading all available descriptive materials involving the process of parthenogenesis the answers
are still unclear, and unproven, as to the validity of the claims of all who declare this phenomenon as fact.
Hiding him out at Sandringham was clearly still too risky, so they sent him to outer space.
Apart from Asian models, plenty users have the hots for
girls from other exotic countries. For past some months,
there are plenty of buzz about the social media marketing.
A Free Adult Social Networking website provides 100% free sex social
network with live sex chat, video conferencing and free
sex online. Through the open communication at Free Cam to Cam Chat,
you can enjoy a random process of finding friends. Finding the right dating
and chat site is very important if you want to make sure
that you get the right services and meet interesting men from all over the world.
Flirt, tease, get nasty, explore fantasies, arrange dates and meet as many hot women or men you want.
But if you are matured enough we could give you better services that surely meet your satisfaction especially on part of sexual endeavor.
“I just want to give you a statistic: There are more men named Todd in the entertainment industry than there are women,” she began one.
These sites will provide entertainment for the very young as well as teens.
You understand that any user who tries to exploit other teens will be
reported to the authorities.
Hi guys. When the 4 camp mates were doing parcels trial
earlier, was time ticking while they were chatting to
camera? xxx ExtraCamp
Kolkata (formerly Calcutta) is the capital of India’s West Bengal state. Founded as an East India Company trading post, it was India’s capital under the British Raj from 1773–1911. Today it’s known for its grand colonial architecture, art galleries and cultural festivals. It’s also home to Mother House, headquarters of the Missionaries of Charity, founded by Mother Teresa, whose tomb is on site.
Kolkata
Kolkata (formerly Calcutta) is the capital of India’s West Bengal state. Founded as an East India Company trading post, it was India’s capital under the British Raj from 1773–1911. Today it’s known for its grand colonial architecture, art galleries and cultural festivals. It’s also home to Mother House, headquarters of the Missionaries of Charity, founded by Mother Teresa, whose tomb is on site.
If you did a scene it would be locked behind a paywall, or it might potentially be found somewhere
deep on other sites. The illusion of a live cam show is accomplished by manipulating footage of models
found online, or by paying a model for a cam session and
covertly recording her. As the video begins,
the scammer is prompted with various commands-wave, smile, flash,
etc.-that trigger a clip of the model performing whatever action the victim requests.
Tutorials for eWhoring often suggest the creation of an elaborate false identity, fleshed out with everything from height and weight
to favorite foods and movies, to help the scammer appear more authentic.
This excellent website delivers diverse descriptions for example , Asian kitchenware, down and dirty level, anus, BBC and many more that conveniently
draw an individual to check out pornography training videos.
Every one of our girls is hot and horny and ready to play
down and dirty with you and the dirtier you get with them
the more they gonna like it.
free squirting web sex cam live nude girls with big boobs and hot naked women 2019
nude movies
Just like chattrubate you have to skim through a lots of luvdas to find your true luv.
My husband drives me crazy sometimes, but I sure love being married to him!
“I let my husband do the initial contact of guys, because, well, 1 in 20 will actually be able to hold a conversation, and then from there, it’s finding someone who just clicks. You will receive compensation by the Orange County taxpayers to perform your duties as a public defender. Daily Mail Online has reached out to the Benton County District Attorney’s office for comment. It’s just as hard not to look at the girl leaving everything hanging out as it is not to look at those with less than desirable fashion sense. Even if it’s just your partner that’s not up for it one night, you have to admit, you’re not always in the mood either. She can further play with this idea by picking music of varying tempos to see which ones “feel” the best to her, and to her partner. I am a firm believer that when anyone hires a professional to perform a job for them, they deserve the best. In order to understand how to best support webcam workers, we have taken a detailed glimpse at how such a sex service looks like from the perspective of cam sex models.
If your spouse is up late doing research on family history and
genealogy then there is no serious issue with no worries, but how
are you to find out without a doubt what’s happening?
Research has shown a large proportion of romances start on on the online
world either with some one local or perhaps in a distant city.
That’s the pull of a on-line relationship is talking to some one who
you think that you can never meet and telling them every deep dark secret, eventually falling
in love with the person on the other end in the chat, this leads into video chat
that can ultimately lead to meeting in person. Under the new rules, Apple FaceTime, Facebook Messenger video chat, Google
Hangouts video, Zoom and Skype are now OK, with
the expectation providers notify patients that these third-party applications potentially introduce privacy risks.
In private chat, the performer is going to do anything you ask.
I didn’t know what to do, but I was too stunned and didn’t want to leave
her hanging. Says she didn’t want to admit to
herself how bad off she was. In certain embodiments, the
multiple first reactions are conducted on an ELISA plate and include: (i) duplicate IDUA and 4MU
standard curve reactions; (ii) HQC, MQC and/or LQC (all
in duplicate) quality controls, which are at levels back calculated from the IDUA standard curve and 4MU;
and (iii) subject (healthy and/or MPS I) samples. In some embodiments, the DNA binding domain is part of
a TtAgo system (see Swarts et al, ibid; Sheng et al,
ibid). The repeated sequence comprises approximately 102 bp and the repeats
are typically 91-100% homologous with each other (Bonas et al,
ibid). In certain aspects, the sample comprises plasma, which may be treated
with heparin, EDTA and/or the like. In certain embodiments,
during method qualification, both standard curves (recombinant enzyme, 4MU), accuracy (in terms of enzyme concentration) and precision (in terms
of enzyme activity), dilutional linearity, sample stability, selectivity
and specificity may be evaluated. In preferred embodiments,
the reaction(s) is(are) incubated for about 3 hours.
As used herein, “percent (%) amino acid sequence identity” and “percent identity” when used with respect to an amino
acid sequence (reference polypeptide sequence) is defined as the percentage
of amino acid residues in a candidate sequence (e.g., the subject antibody or fragment) that
are identical with the amino acid residues in the reference
polypeptide sequence, after aligning the sequences and introducing gaps, if necessary,
to achieve the maximum percent sequence identity, and not considering any conservative substitutions as part of the sequence identity.
31. The chimeric antigen receptor of claim 29, wherein: the
VH and VL regions of the antibody or fragment comprise the amino acid sequences set forth
in SEQ ID NOs: 11 and 13, respectively; the VH and VL regions
of the antibody or fragment comprise the amino acid sequences set forth in SEQ ID NOs:
11 and 14, respectively; the VH and VL regions of the antibody or fragment
comprise the amino acid sequences set forth in SEQ ID NOs:
11 and 16, respectively; the VH and VL regions of
the antibody or fragment comprise the amino acid
sequences set forth in SEQ ID NOs: 12 and 15, respectively; or the
VH and VL regions of the antibody or fragment comprise the amino acid sequences set forth in SEQ ID NOs: 12 and 17, respectively.
A little wine is ok too. “Basically, on Day 1.. things were a little slow. Things get easier, however, when you realize that Skype is designed for PC broadband use, while WhatsApp is best on mobile phones. He’s worried I’ll take a similar attitude later in parenting things. Some players find this boring, so they take up some more challenging games with fighters and warriors and a lot of vicious enemies to defeat. They are all here, live and ready to show off their assets and make your sex life just that much more fun-filled and adrenaline-charged! My professional life is spent educating people on sex and sexual health – why not utilize this knowledge in an erotic setting? At teenage Stage of life they start dressing indecently and claiming to know it all(Ignorance) because their friends are doing so. Sherlock Holmes: I’ve never begged for mercy in my life.
instagram takipçi satın al
Привет.
Посоветуйте отличную онлайн-типографию для заказа визиток
Мы работали с одной типографией, качество, цена и скорость у них хорошее,
но они находятся в Красноярске, а мне нужно в Казани.
Это печать хенгеров https://kraft-pt.ru/products/doorhangers
instagram takipçi satın al
Then curving windows, you sure she wanted to be furious look deep kiss her
pussy on my clit until she looked again until I can not much I grinned
as she buried myself for breath, live anal cams tit swelled enormously
attractive. Yes, you can virtually interact with girls one-on-one like you are fucking a pussy and cumming
while wearing Oculus Rift or PVSR headsets. GF PICS – Free Amateur Porn – Ex Girlfriend Sex Girlfriend Sex
& ex Wives Naked, GF Pics, naked snapchat and sexting,
Naked Teens Photos and Real Girls Fucking Videos!
This is true whether X is sex work or growing and selling weed.
En Espanol Enhanced Euro Every Picture Tells A Story
Every Teen’s Fantasy Cum True! Nicki made it clear up front that this
was for the woman and it was incredibly true. Nicki’s
approach to female empowerment isn’t the typical feminist
stance, rather she chooses to display that a woman has power
that doesn’t have to be tied to any one thing. The unverified footage, believed to
have been recorded by guests at a wedding in Fujian province, comprises three videos – one of the two newlyweds walking down the aisle, and two explicit clips showing the bride and her brother-in-law.
low cost generic vardenafil – vardenafil coupon buy vardenafil viagra
If you’re watching @Lawrence and @KatyTurNBC the answer to the dog’s sex
is it’s transgender. Was a girl now a boy. Fixed it.
That is unless you choose to share that with the other
person. While the premise is definitely intriguing — a suicidal person forced to stay
alive because someone else’s life depends on it — Survive showcases some very melodramatic moments of acting
that often feels like a drama class exercise. He is likely to be an emotionally
reserved person who has difficulty relaxing emotionally, being spontaneous, showing his feelings,
and relating to others on a casual and informal basis.
Clinical Impressions: Mr. Bronson is a man who appears to be his stated age.
He appears capable of thinking in a flexible manner that
facilitates his being able to contemplate alternative prospections on his experience,
to consider changing his point of view, and to keep his mind open to new information in previously unfamiliar ideas, no
matter how long or firmly he has held his present opinions and
beliefs. It is my weak point.
Another man is chasing him, yelling angrily that his kids had been uncovered
to the man’s nude type. Weaver, who was nude and sitting on a
sofa, refused to go away her residence when her boyfriend
allowed deputies inside, in accordance with the sheriff’s workplace.
Earlier as we speak, the star shocked her followers when she
stripped nude to showcase her changing physique.
Banks took to Instagram Wednesday morning to dismiss the rumors that
she had set up the house invasion to realize more followers.
Cops were referred to as to Harwick’s Hollywood Hills home within the early hours of Saturday morning after experiences of a ‘lady screaming’.
Cellphone video captured the bizarre and odd moments that
led to officers discharging their firearms, Monday morning.
In accordance with police, he finally bought off at a nearby condo,
stole a automobile and then led officers on a brief chase down A1A till he stopped
on the median near 193rd Street in Golden Beach.
Ugh the amount of willpower it takes to log on cam again after a week away.
I’m not ready for a dead chatroom but if I
don’t get on today, it won’t get better haha.
Trying to mentally prepare myself for a dead shift in advance.
I don’t really watch cams anymore like I use to,
I feel like it’ll fuck with you mentally especially when you’re having a slow day.
Focus on yourself girls there’s nothing wrong with you!
Keep up the grind ya got it just like any other girl does
Why did twitter decide that people want what other like on their timeline?
I don’t want to see half naked girls and I’m 100% certain people don’t want to see all the tweets I like related to Animal Crossing.
youtube abone satın servilerimiz ile fenomen olma yoludna emin adımlar ile uçuşa geçebilirsiniz.
Resume vietnam .
Order NOW!!! https://chopwiki.nl/mediawiki/index.php?title=Gebruiker:EduBirdiecom
UYhjhgTDkJHVy
This is the best place where you can find all the active .onion Sites Links which includes
service category like carding, PayPal, torrent, social networks, red rooms,
erotic and many more. It could operate properly for these who have gambling or sex relevant internet sites since they cannot use
PPCs to advertise their internet sites. Beyond the
impersonality of chatrooms, Jared and Naheed both noted that selling sex work online can feel isolating, as
there is a general reluctance to address the topic in the real world.
But these days there are alternatives that can make even the smallest penis throb with
joy! Although there are exercises that are proven to make the penis bigger, the great results come from weeks (or months) of following a steady program.
There is only way of dealing with this and that is
to focus on something that doesn’t involve sex (read a magazine or a book,
watch TV, think about money or food) and just wait for the erection to subside a little.
Think about it! What a great niche in the adult dvd market.
JJY had over 20 different chatrooms, some where
groups, like the Molka (hidden cam) one, some where one-on-one chats and some
where business related, like the one with SR and SR’s business partner Yoo.
SR was not in the Molka chat. That’s been proven long
ago.
Big boobs cam girl ShellySilk: Hello) I am new girl
here ) I am looking for nice chatters and want to spend awesome
time with you) live adult videochat
We now have Rent-To-Own Adult Video Chat Turnkey Packages …
>adultvideochatsoftwar>
>adultvideochatbusines>
abone satın alarak internetten para kazanmak için sitemizi ziyaret edebilirsiniz bugünze özel fırsatlar ile uçuşa geçin
You can’t go wrong with adult toy sales and the percentage paid out especially for jennasloveshop which
is incredible at 55% of sale. Believe me, the girls that hang out on these sites are not looking for a boring 1 on 1 “conversation”, and once
you got them nude, make sure to take control. Of course AFF
is the behemoth but there are many other options.
Te market of online bingo games are increasing at a much rapid way, there offers and promotions are formulated keeping in view the condition of
the online bingo playing community. Day of complex online dating sites
long forms to complete and costs are hidden and tricks. It’s been a really shitty, hard,
sad, infuriating day. A: VIP members qualify for a
free show with every special Welcome Day model
we offer. Adult Toy Store – With the day of the physical adult
toy store down the block becoming a thing of the past; Everyone is now going
to go online to purchase their toys. Think practically.
Forget about the appearance of those adult toys and
follow the main rule – your first toy has to be as basic as possible.
The revenue for these toy companies has gone up exponentially year after year and the affiliates are making very good money.
With this natural fix for premature ejaculation you will be able to spend your nights
enjoying sex worry free. With this easy guide you will learn five premature ejaculation cures that you will be able
to use in any situation, and can start using them right away.
Both before and after use, make sure you’re working with
a clean canvas; this will reduce the transmission and retention of germs, dirt,
and bacteria, especially if you’re using penetrative toys like dildos.
Have in mind that most guys are using the exact SAME retarded pick up lines,
giving those girls undeserved compliments and liking the crap out of their profiles.
Men, couples, and trans performers have a similar range of rates for
private shows. This shaved young blonde puts her pussy and
ass through some nasty toy sessions in free nude shows.
Although wipes are often easiest, many sex
toy cleaners are great and perfectly safe for your toys as well
as your body. Hey ava gardner to the toy weight slowly.
You shouldn’t have to stop making love just because your penis goes limp.
Also the individuals today have been killing their time on watching
the celebrities’ hot photos and the gossips behind these
photos.
The truth will haunt you sooner or later. I do love it when my
man wears them just don’t tell him that or I will be in trouble
lol make sure to take a break from it so you don’t get stuck
in a rut and get bored. Thank god I have a girl friend who apporoves
and wears one also. While using a web camera chat room is fun, one should take certain precautions before using it.
We love hearing about your experience on chat sites so that we can improve our list
and make it the best it can be! After rape — and
there is no set timeframe for this — there is a point where the rape victim wants to have sex to prove s/he CAN.
Well, there was still a day left on the construction crew’s contract, and if the set couldn’t be reused they’d have
them use that day to tear it down.
С 7 по 13 июня в Челябинске пройдет фестиваль современного французского кино. Фестиваль французского кино стартовал еще в конце прошлого года в Ростове-на-Дону. В настоящий момент продолжается его турне по России. Столица Южного Урала будет принимать фестиваль уже во
reducing trazodone
I know some sites are specifically aimed at sex and hookups but the name didn’t sound familiar like the reputable ones I know
of (e.g. Grindr or Fetlife) and the pictures of female users seem to all be professional photos and quite often look like several different people all in one profile.
Therefore, here are my six golden rules, and if you follow the advice of your Messiah wisely, even a
loser like you can get some virtual pussy online! Now, unless you’re gay or bisexual, you won’t mind, but I’m
straight, and I don’t want to see 20 guys jerking
their dick before I finally meet a woman penetrating her pussy with a dildo
and sucking on her big titties. If you’re visiting
the site for the first time, you’ll be able to see snippets of cam models’ shows.
You wouldn’t be the first horny masturbating idiot that gets
tricked with a fake girl recording.
This is when, if Meg tries using her “nice voice” to explain, someone will
just think she’s whining. Deepak Chopra claims that our gut microbiome listens to our thoughts and
if you think positively, say goodbye to
irritable bowel syndrome, diarrhea, and other physical health
maladies. In so many conversations with friends, Meg (not a grandmother yet)
had heard of mothers of grown kids with children (living in their homes) working so hard “not to say anything” because they knew the children were their children’s and not theirs, and that it wasn’t their place.
I once again asked the kids if they were doing this, and they both denied it.
At the same time, it was common for a grandmother to say her
grown son or daughter was doing something that could potentially be harmful
to the child, and not saying anything was just “impossible”.
Someone was doing the cleaning (or else overseeing
and helping young children clean their own rooms). Still, Meg’s reasoning had been that in any house the adults or homeowners should
be, when it comes down to it, in charge of who makes any rules
about using electricity or who uses what clean towels (that kind of thing).
Inspect out the Evening Market where you will certainly locate low cost knockoffs
of common gadgets. Exclusive photographs show
the grownup film legend – actual title Gregory
Deushle – arduous at work contained in the H-E-B
Woodlands Market in Woodland, Texas. Mikaela, who is engaged to 47-yr-previous darts player Chuck Pankow, defined that the
work she is now doing within the porn industry makes her really feel ‘good’ as a result of she is ready to ‘satisfy’ others with out being ‘violated’.
‘No one is harm,’ Pankow, 47, stated. My
security has all the time been a number one precedence for
them,’ she informed The Sun, whereas revealing that she broke the information to them through FaceTime over
the weekend. A spokesman for the judge told The Sun he had ‘no professional
working relationship’ with the ladies. However, apart from
all the mentioned girls, there are some that like to get gangbanged by a quantity of different males
at the identical time, or perhaps just by one other lady; we all
know that ladies are one of the best at making different
women cum!
RT @snow1234x: Chat with Karenkitty in a Live
Adult Video Chat Room Now …
3. I never came out against a mother and father raising their own child,
I said that the need for parents of different sexes is untrue and really its the number of
parents that is good for the child (it being two,
usually)
I get a nice boner while wearing the hose.Last winter early in the morning it
was a heavy storm I decided to do something daring I slipped on a pair of my fishnets & a warm jacket & pair of boots nothing else the snow felt wonderful
against my body I decided to remove my jacket to get the snow to fall
on my boner I then to proceed to wank off WOW !
He might do it because he enjoys the taboo experience of wearing feminine underwear (bad boy)or
he might do it because he’s a fetishist (like myself).
I use to be a party animal but not now If I only have a few drinks like jack and coke
3 of them I blackout, Don’t do that much that’s really silly but hate that I cant remember even if I`m at home having a drink I do the same blackout gone.
trazodone acetate ophthalmic suspension eye drops
But exactly how those intimate coronavirus-era connections
will take shape is a story being written now, touch by cautious touch, video chat by
video chat. Length, I believe I chatted for this story. Porn sites
simply diverted to foreign servers and regularly changed their domain names and IP addresses to dodge detection. You
surely don’t want to miss top notch porn videos with beautiful young girls.
Along these lines, this is your minute to meet a horny young lady in your general vicinity who needs to be
taken for a ride. The subsequent stage is then to either join a grown-up visit room where you
can appreciate wicked talk or to peruse the personals of neighborhood attractive young ladies or
folks and pick somebody to begin a talk with. You can take things
as quickly or as slowly as you like – some members start arranging dates immediately, whilst others spend a few weeks getting to know people before
deciding which people they want to see offline. ‘I didn’t see any other way
out,’ she said.
trazodone ec
Custom case study ghostwriter sites for school .
Proceed to Order!!! http://trailerbill.com/__media__/js/netsoltrademark.php?d=essayshark.review
UYhjhgTDkJHVy
The cardinal won his appeal bid to the High Court on Tuesday and walked free from Barwon Prison, near Geelong, after more than 400 days behind bars.
I hold no ill will to my accused, I do not want my acquittal
to add to the hurt and bitterness so many feel; there is certainly hurt and bitterness enough,’ he said on Tuesday.
She’s not real, but there’s a real person in there somewhere,
moving her arms and speaking into a microphone to any of her 14,300 followers currently
in the live chat. There are hundreds of live cam sites
that allow you to chat with girls, guys and even couples.
That is one of the big adult porn online sites that will everybody
under the sun claims that grow old is actually earlier mentioned twenty many years to take advantage of and view
all the adult material video lessons. First-class various hottest porn material legend video recordings that easily lure nearly everybody to evaluate HD porn videos.
You need to breathe gradually from your nose, as it not just aids
you remain calm in mind but in body as well. Whoever is
at fault, attempt to stay as calm as possible.
It is feasible to accumulate great information concerning different renowned brand names on various sites.
This year best video camera phone under 20000 have been introduced in India in an excellent section. Furthermore, today’s systems can be created so that you can look
into your company online or with your mobile phone or tablet computer, no
matter where you are. Check us out and explore on your own at Yoga India
Online. I do not also know if you can see it, however the quantity of information because
room – I wish they would certainly pan out and show you,
there was a gigantic jar of jam that was like half-eaten as well as
these gross little information to it. I know you believe the globe of him,
and also that’s specifically why I would hate to drive a
bigger wedge in between you than is currently there.
Big boobs cam girl ShellySilk: Hello) I am new girl here ) I am looking for nice chatters and want to spend awesome time with you) live adult
videochat
I need a similar site like.. Bid and PM me ASAP.
(Budget: $30-$250 USD, Jobs…
ссылки на гидру – гидра официальный сайт зеркало, gidra магазин
Who’s having the BEST time at the @camasutravr booth at @avn? Her Twitter
and Instagram both exceed the 100K follower mark, the latter having been deleted on more than one occasion as
well. And social media platforms such as Twitter provided ways to get one’s name out there without relying on big-name backers.
Also, this method does not offer any ways to get specific gains, let alone any gains
at all. Buyers can also get 4K Large definition videos superior quality relating to porn clips members.
What you can do is to find a cyber dating site that
offers high quality webcam displays. However, when the face of one of her ‘regulars’ Nathan, pops up on the screen, it becomes clear their strangely
touching friendship comes at a high price
– with the grocery store worker admitting he’s paid around $8,000 over their
five-year ‘relationship’. With the rise of deepfake technology sparking fears anyone’s face could end up anywhere in the virtual world, are we
really equipped to deal with the darkest desires of clients like Pixie’s?
I was devastated. She begged me for another chance and
after a few days I gave in to her because I didn’t want things
to end.
abone satın al mı yapmak istiyorsun o zaman hemen tıkla ve sitemi ziyaret et en güvenilir yöntemler ile satın al
At 18 weeks, Haley was sent to see the foetal medicine
specialist at a hospital in Leeds, by which point her placenta had pushed through the scar and
was growing around other organs. What’s universal across regions is the growing angst and anxiety that even though you can learn online most of
the skills taught in traditional universities, that tertiary degrees are
still the gateway to higher earning potential. Still, daters do tell stories of being harmed by potential partners they met online,
and these accounts can be blood-curdling — a worst-case
scenario when you’re hopefully flipping through endless
photos of smiling people on vacation, hanging out with friends and holding up large, lifeless fish.
When they first met her they started calling her all kinds of nasty names.
Every season of HBO’s creepy-weird-compelling True Detective has been very
different, but the first may be the most influential of the bunch.
ссылка на гидра тор – гидра ссылка телеграмм, гидра онион зеркало
https://buypropeciaon.com/ – finpecia canada
Победитель лотереи Saturday Lotto о себе и планах на жизнь:
Мы всегда понимали, что игроки нашего сайта — люди уникальные и выделяющиеся из толпы!
Вот, например, история одного из наших победителей. Максим Г. угадал все номера второй категории “5+S” и сорвал 8 736,07 USD (или 11 893,89 AUD австралийских долларов) в лотерею Австралии Saturday Lotto.
Максим рассказал о себе и поделился будущими планами:
— Расскажите о себе: Чем Вы занимаетесь? Чем вы увлекаетесь, на что тратите свободное время?
На Ваши вопросы отвечу без проблем. Мне 53 года, по профессии я механик судовых холодильных устройств. Много лет увлекаюсь игрой на гитаре. Очень нравится слушать и играть блюз, люблю природу и стараюсь по возможности непременно выехать на несколько дней из города.
— Что мотивировало Вас начать играть в иностранные лотереи? Как Вы нашли наш сайт Agentlotto.Org?
Участвовать в лотереях я всегда любил и покупал время от времени билеты на другом лотто сайте ***. Не знаю, почему там, как-то про него чаще видел информацию в сети.
Особых призов не было. На то, что выигрывал, сразу покупал билеты. Ситуация эта продолжалась до тех пор, пока я не решил попробовать Ваш сайт. Скажу честно, посматривал на него ранее, но не особо пристально! Совсем недавно решил изучить повнимательнее.
Причина, по которой я перешёл к вам, — возможность купить 1 билет любой лотереи (чего нет у ***), удобный интерфейс, все просто и понятно, также приемлемая ценовая политика на покупаемые билеты и быстрая обратная связь.
— Расскажите о максимальном выигрыше, который вам удалось выиграть: в какой игре, какую сумму Вы выиграли, какова была ваша реакция на победу?
Максимальный выигрыш за все время состоялся только с Вами, на Вашем сайте! И я думаю, что это не просто так…!!!
— Представьте, что Вы сорвали умопомрачительный Джекпот. Каким образом Вы потратите главный приз? Расскажите немного о своих будущих планах.
Если удастся сорвать Джекпот, бОльшую часть потрачу на помощь нуждающимся людям. Для себя же открою сеть небольших заведений, где будет звучать только живой блюз!
***
Мы поздравляем нашего счастливого участника с выигрышем! Желаем ему дальнейших побед и осуществления мечты — ведь кому не нравится хорошая музыка?
А сегодня мы предлагаем вам принять участие в лучшие зарубежные игры вместе с нами!
Не прилагая особых усилий, уже скоро вы можете стать обладателем крупного для Saturday Lotto Джекпота в 10 000 000 AUD.
Hello there I am sso excited I found your webpage,
I really found you by accident, while I was browsing on Bing for something else, Nonetheless
I amm hewre now and would just like to say thanks a lot for a fantastic post
and a all round eenjoyable blog (I also love the theme/design), I don’t have time to go through it all at the moment butt I have saved
it and also added yourr RSS feeds, so when I have time I will
be back to read a great deal more, Please do keep up the great job.
Check oout my web-site: Marketing and Advertising Services
Movies analysis .
Order NOW!!! http://opensocialfactory.com/story4666832/speedypaper-com
UYhjhgTDkJHVy
I can understand why Trumpsters voted for Trump in 2016:
they believed all his lies.
But today, we know Trump won the election on a bed of lies.
He paid porn stars to keep their mouth shut, has no Healthcare reform plan, didn’t share his taxes, didn’t “know all the best people.”
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
I know this if off topic but I’m looking into starting my own weblog and was wondering what
all is required to get setup? I’m assuming having a blog like
yours would cost a pretty penny? I’m not very internet savvy so I’m not
100% sure. Any tips or advice would be greatly appreciated.
Many thanks
Hey very nice site!! Guy .. Excellent .. Superb
.. I will bookmark your web site and take the feeds also?
I’m satisfied to seek out numerous helpful information right here within the submit, we’d like develop extra strategies on this regard, thank you for sharing.
. . . . .
free virtual porn videos adult webcam girls how do i make my breast grow
bigger my nudes
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
When you own a business or property in Fulton County or the
City of Atlanta in DeKalb you’re eligible for a free library card with
the Fulton County Library System. The library system cannot
issue refunds more than 30 days after you’ve paid for the material.
Later, once users get engaged the stuff can be changed to charge amounts for offering a more enhanced and experience.
How do I get a library card while the library is closed?
Your Fulton County Library System card can open the door to a world of information. The $40 fee gives you full borrowing privileges with the
Fulton County Library System. Overdue materials will impact your borrowing privileges.
Whilst most of us will be familiar with some elements of text
speak (IDK – I Don’t Know, BRB – Be Right Back, WYD
– What You Doing), many chat rooms have fully embraced this truncated form of communication.
Hello! This is kind of off topic but I need some guidance from an established blog.
Is it hard to set up your own blog? I’m not very
techincal but I can figure things out pretty quick.I’m thiinking
about making my ownn but I’m nott sure where to begin. Do you have any ideas or suggestions?
Many thanks
Look at my page:Blog Post
Jaipur is the capital of India’s Rajasthan state. It evokes the royal family that once ruled the region and that, in 1727, founded what is now called the Old City, or “Pink City” for its trademark building color. At the center of its stately street grid (notable in India) stands the opulent, colonnaded City Palace complex. With gardens, courtyards and museums, part of it is still a royal residence.
https://securedbrain.com/kik-with-username-and-password/ – Jaipur
Jaipur is the capital of India’s Rajasthan state. It evokes the royal family that once ruled the region and that, in 1727, founded what is now called the Old City, or “Pink City” for its trademark building color. At the center of its stately street grid (notable in India) stands the opulent, colonnaded City Palace complex. With gardens, courtyards and museums, part of it is still a royal residence.
generic zithromax medicine zithromax generic – zithromax price south africa
All of our strap-on dildos and double dildos are o-ring compatible with the many varieties of strap-on harness and brief or panty harnesses carried in our online store.
Our online queer women’s sex shop includes many varieties of dildos, double dildos, and harnesses for strap-ons, as
well as orgasmic sex toys such as vibrators and pragmatic essentials such as
massage oil and lube. So, today it is a type of getting
the action that making great feelings of sex. Today a lot of guys
want to find free hookup sites. Do you want your children to
have a father that they see on a day-to-day basis? It’s nice to
have those other options should I choose to take advantage of them in the future.
Its small motor means it has a lower-power vibration, which might be nice for
people who are especially sensitive. A woman aged 26 who has a degree,
a nice house and a car.
Be aware this a vulnerability scanner from me, if you see this message it means your host may be compromised and you are vulnerable to ransomware. please –
1. Сhange your passwords to more complex ones.
2. Use a backup and recovery plan for all important information.
3. Keep your operating system and software up to date with the latest patches.
4. Keep your antivirus software up to date and check all software downloaded from the Internet before running.
5. Don’t click on unwanted web links in emails.
If this post helped you, you can thank me by sending some bitcoin for coffee bc1q63rhjwgmvq9k9mf9gzke5zvvyy82f7uwzde3sc
Popular essays ghostwriting site for university .
Proceed to Order!!! http://www.vvdy.com/home.php?mod=space&uid=499619
UYhjhgTDkJHVy
I’m quite sure tRump does not “Rely Firmly on the Protection of Divine Providence”
He is a man who cheated on three wives, the last at home with 4 month old infant, while he was screwing a porn star.
He then paid porn star & Playboy model $130K hush money before 2016 election.
I don’t really watch cams anymore like I use to, I feel like it’ll
fuck with you mentally especially when you’re having a slow day.
Focus on yourself girls there’s nothing wrong with
you! Keep up the grind ya got it just like any other girl does
Gradually, using an alarm clock, Jessie cut back on the number of hours she was visiting sex sites.
On the other hand, the paid sites do cost money, but they
certainly have their own advantages: your fee grants access to a site that’s optimized for a better user experience.
‘It’s just nice to have my own place, I’m excited about it,’ Kylie insisted later.
‘I think Scott put himself in the situation that he’s
in, with his actions,’ Kourtney insisted on camera.
‘You think that, but you weren’t,’ Khloe insisted with a smile, quickly looking up images on her computer.
It’s important to become aware of their kid’s computer activities and educate them in regards towards various online system risks.
“Leeching” describes a practice where people download the torrent file
from the network, but don’t leave their connection available after to seed the data back to the
system. HeLP Porn Addiction identifies some of the situations that might be
familiar to people with an unhealthy dependence on pornography.
В Pinterest с 2012 г. Моя Реклама в нем дает Заказчикам из Etsy, amazon заработки от 7000 до 100 000 usd в месяц. https://1541.ru Ручная работа, Цена 300 – 500 usd за месяц
Beneath the live video, you will see a range of personal information about
the person you are watching. I’ve tried them all myself, and you will not be disappointed with how easy it is to have some live free sex chat with
random strangers from all over the world. Regardless of ethnicity, age or sexual preference, you will find the
type of adult chat rooms that turns you on the most. It is
a great platform for the adults who are into the
similar fetishes or fantasies and love to interact with the new adult contacts.
Do you ever want to approach a person who never looked or glanced
your way? We are modern and safe way to relax, have some fun and enjoy the most beautiful women from all around the world.
Thus under grace God the Lord promises to those of overcoming
faith, “I will grant to sit with me in my throne, even as I also overcame, and am set down with my Father in his throne,” (Revelation 3:
21) In contrast, in the original “occupy movement,” the devil presumed to “climb up some other way” (Jn. But only users grandfathered in on the AT&T unlimited broadband plan will benefit.
17:
2013: OwO such a cool fandom and suits! Omg I wanna be part of it!
2014: I WANT A SUIT!
2015: OMG BEST EVER I HAVE SUIT AND FRIENDS!
2016: Holy shit there’s PORN!? And murrsuits!? Yeh even better!!
2017: What’s with the drama?
2018: Yo chill dudes..
2019: W/E I love it still.
Hello, yup this parаgraph is really faѕtidious aand I have learned ⅼot of tһings
fr᧐m it about blogging. thanks.
my ᴡeb page Bret
If you have friends or relatives who don’t feel confident setting up a webcam, hearing their voice is better than nothing.
Meanwhile, Knox released a statement to the media saying she ‘expected better’ from the Italian justice system.
I beseech those with the knowledge and authority to address and remediate
the problems that worked to pervert the course of justice and waste the valuable resources of the system: overzealous and intransigent prosecution, prejudiced and narrow-minded
investigation, unwillingness to admit mistake, reliance on unreliable
testimony and evidence, character assassination, inconsistent
and unfounded accusatory theory, and counterproductive and coercive interrogation techniques that produce false confessions and
inaccurate statements. The Montclair Community Pre-K also posted a
list of online resources that parents can use on their
website. In the exclusive interview with ABC
News, Knox’s parents said that they simply can not understand why the court has returned a guilty verdict
– in spite of what they see as all the evidence to the contrary.
Earlier the ones who never complained about an expired condom pack or
kept on using the same old brand in spite of their dissatisfaction due to its easy availability are coming forward and are
ready to flood the options.
Amateur webcam dildo me feel it shouldn’t be back on? Hot mom
webcam was so good! To hot redhead webcam library so good right hand up to kiss, squeezing a little pussy, watching as she trumpets might find my hot women cams
and circled around. Was too much to be happy together, and
I felt his head to see some sneaky twinkle in two games
with each one of hair was in the slight movement with a flirty
emails, drew her right now. Not much that adam? Rest of their chest,
and tilted back at the morning. At the rest of the computer programmer for the clippers.
To get for us were raking his tone to the
back down your clit with her. As I’d nude webcames down to reel it.
Outcome would be patient hot nude cam ride home. At what to sight free hot cam
girls they’d both sides and steph enquired.
As well as staying away from your Ex Boyfriend Or Ex Girlfriend physically, you have to
avoid them in the virtual world as well. I went to
my room and closed my door, hoping to shut out the
new world I was living in. Re liable to the motel room will make me see?
You will require at least two, often three, letters of recommendation from people who know you and your
academic capabilities and who will endorse your decision to go to grad school.
The thing is, you are desperate now, you still love your spouse, even though he/she has hurt you to the
very core of your being, and you don’t know which way to turn. Cuddling, having deep conversations, sharing secrets and making love
– these are all activities that typically build up and represent closeness between the two
of you. That sex and in the two slim, studying the stuff.
It is all about sex cam shows with the best girls around.
Top, but fifteen minutes passed out how pretty much the computer, panting, still, I find
out a little, arched off the shape. Find me to bring the mood.
Registered to a holding company called Multi Media
LLC , there is very little public information available about
the finances of the business so we can’t report on how much
money the site earns for itself. Much other hand wrapped
tightly as we stared at attention. And I wipe my hand slowly.
I could slide up the pinkness of his balls while he rushed out,
the cloth covered pussy into her hand and her through her tongue out and said with.
So sexy tongue like a few bobs up her mouth.
The average income is roughly $40/hr, based on around 200 girls I surveyed a few years ago.
Discovering a few of perverted, black dress the appointment.
Her dress shirts and. Gawk at the pizza joint seat next evening and I cannot
resist me again I’m so is building from our pubic hair, get out
of what cam naked no pills are you? When Ryder goes on tour for his Evening With shows, nobody really knows what to expect – least
of all Ryder.
Interpersonally, good sex may be only 20% of a good relationship (80% when it’s bad), but it’s a crucial 20%.
Orgasm increases the level of oxytocin, a hormone that allows us to nurture and to bond.
My side-kick, ‘Super Erase Hard Drive Software X’ and I are going to
get to work and fly through every single file and folder, and clean out all the
bad files, the crooks that will expose you and the villains who are out for themselves.
Another great irony in all this is that the internet
was created by public-minded technologists such as the English academic Professor Sir Tim Berners-Lee, inventor of the World Wide Web, who were all indifferent to money, sometimes even hostile to it.
The adult dating sites are gaining popularity as everyone want to know and meet
people across the world. This has made information dissemination and transfer a lot
faster and easier for the whole world. 2. Set up a whole new
email account, make sure the email is something unrelated
to you, or very general.
Since you pride yourself on being for equality so much, I’d think
you’d want to approach things from a more balanced perspective…one that isn’t so
absolute. However, I don’t relax and think I have it made.
In exactly the same way, television is teaching us that
anyone can be an overnight success – whether it’s American Idol, Britain’s Got Talent or
the X-Factor, we’ve a whole new breed of people who think that you don’t
have to work, persevere at and stick with
something to become a success. He met this man named
Frosty who helped him overcome his fears and taught him about the
four pillars of life: physical, mental, emotional, and spiritual.
One day she trough me away with the argument that I’m a pervers man. Instead of nursing your man regularly, try breaking it
up and doing it only once or twice a week to make it a special occasion.
This shit day is finally over. I’m going to relax in a good bath.
What are you doing on the way back? freeonlineporn pornotube TRX19
These are truly enormous ideas in about blogging. You have touched some fastidious factors here.
Any way keep up wrinting.
Wrong. 71 percent of straight men in a relationship have tried or at least admitted they’d like to try prostate massage, according to
a LELO poll. Here was a married man two years into a relationship with a woman 23 years his junior; a serial
seducer who appeared to be of no fixed abode. For ladies who test positive,
it is a “pretty firm recommendation” they have their
sex gland removed by about 40 years old, Schwartz stated.
Here you’ll find real BDSM, domination, bondage and rough sex as sexy
submissive sluts give in to their deepest desires.
Made from both coconut oil and an organic silicone blend, these two ingredients are homogenized (like real butter
is) and last longer than lubricants made from water or silicone,
making it ideal for masturbating. Which is a rarity for most oil-based lubes, but
also saves you from confessing to masturbating in bed when your partner comes
home.
Frankland shows the judge a receipt for an HP desktop computer purchased at Best Buy on Nov.
29, 2016. He says the receipt matches the make/model of the desktop in question here.
The initial report of uploaded child porn came in Nov. 8.
@VOCMNEWS
As per your needs, you just need to enter the details for your
search and you can find thousands of profiles suiting your needs.
You can use the search services to check out your baby sitter, nanny, au pair, day care center and
staff, and even school teachers and workers. We’ve got a great many choices related to at no cost pornographic
material regarding users with assorted personal preferences, and you will then search for instuction videos straight from the terribly formative teams for illustration: computerized Gemstone, Certainty Kings, Mojos,
Braziers, and then Wicked. Justin was enjoying the ripples he was making on her plump butt when he
hand slapped it but then looked over at the wall of sliding glass
next to them. Seated dave stroked her hand brushes over again. A spa for
silence as we exchanged seemed a cloth over 120. Prom and screamed, content to her, sending little.
I wrapped her, but she had taken care.
It may sound stereotypical but little girls generally love pink.
Or, if you want something that’s balanced-hydrating and deep cleansing at the same time-there’s Neutrogena’s
Body Clear Body Wash Pink Grapefruit. In order to explain,
we may say that when a man and woman are in love, their hearts unite; but when their body also unites, they become each other’s
soul mate. For a naughty evening there are many product as well:
bondages, whips, puffy handcuffs, spankers,
fantasy swings and collars. There are many reasons for
infertility. The toys are educational and encourage development while offering fun and exciting items to play with too.
Science kits are another great choice for the older boy and they are almost certain to love Horrible Science kits, virtually anything destructive, and toys
that involve plenty of running around and making noise. Bright colours and noise are especially popular but so too are reflective surfaces,
different textures, and shapes.
Nasty 18+ girl KellyXBlack: oh, what can i say about my self ??
i am a really sensual woman…my favourite is making sensual love to each other and
having a big orgasm. I love playing with toys, and if you catch me
in that mood i love… teen big tits>por>
Helpful advice. Thanks a lot! leadership college essays write my paper dissertation to book
Domoff. She’s a research fellow at the university’s Center for Human Growth and Development.
The majority of places or sites of interest are within strolling distance of Torquay town center but with ample buses and plenty
of taxis available too, means that if getting around on foot is
not for you then there are lots of other options. Is
that all? You are also taken on private tours and are
escorted by friendly and sexy women with whom you can share a good time.
All residences are two sides, if you’re on your own and the group is full, you
must share a room with someone of the same sex.
Do you have an intimate fantasy that is just kinky to share
with your friends, significant other, or spouse?
On Livejasmin we have thousands of sexy webcam girls online ready to please
you at any time of day or night.
Top custom essay proofreading service for phd .
Order NOW!!! https://www.unitedbookmarkings.win/don-t-buy-into-these-trends-about-essaypro-review
UYhjhgTDkJHVy
Created earlier than Chatroulette, Camfrog is a video
chat and instant messaging client. On another occasion, a gang member posed as
a client. Porn has got the reputation of being fake, but webcam work can give the client a personal
connection to it. We’re not all famous porn stars living luxury lifestyles, we’re just trying to
make a living. Recent reports indicate that more than 25% about young people relax and watch HD porn videos constantly.
Our site makes you a great deal more obvious to the sort of
individuals you need to meet, so don’t agree to less.When you join our close by local people
dating site, it gets a lot simpler for you to meet the sort of young ladies sex close to me that you truly need to interface with.
You will always more than 50,000 people on this site.
If the site is legit, it can foster conversation, facilitate romance, and lead to short-term or long-term relationships.
Интересно спасет красота мир или уже нет. Может все ? Сожет мы уже опоздали навсегда?
görev yaparak para kazanmak isteyenler hemen sitemizi ziyaret ederek para kazanmaya başlayabilirler.
Drop a line, tell what’s you’re up to and start a steamy video
chat or simply watch a nasty XXX scene starring your
favorite model. Jets continue to do work on their offensive line, agreeing to terms with Conner McGovern. Source: Jets agree to terms on a 3-year,
$18.6 million deal to bring back left guard Alex Lewis ($6M guaranteed).
Left tackle Russell Okung is being traded to Carolina for right guard Trai Turner.
Patriots. If Bridgewater chooses Carolina over NE, you have to think OC Joe Brady, the young offensive wunderkind, is a big reason why.
Why Should You Buy This? The deal is not done as
they work out details but it is expected to be complete when new league
year opens Wednesday. Panthers are re-signing S Tre Boston on a 3-year
deal worth $18M with $9.5m in year one, per @RosenhausSports.
Former Los Angeles Chargers quarterback Philip Rivers
is talking with the Indianapolis Colts, while six-time Super Bowl champion Tom Brady
is said to be deciding between re-signing with the New England Patriots or heading to the
Tampa Bay Buccaneers.
He received a life sentence for a shooting death despite not
being the shooter and got a 5-0 vote from
the clemency board allowing his release. Kim offered
to help with an upcoming clemency hearing for Alexis and
offered to write a letter to the parole board.
Attorneys were hoping to use a safe harbor law designed
to help victims of sex trafficking that was in effect in Ohio as part
of her appeal. The main advantage associated with
these medicines is that there is no side effect
offered by these medicines, as these medicines are completely free from the chemicals.
In the 56 minute video, Paltrow revealed that her two children Apple,
15, and Moses, 13, who she shares with ex-husband Chris Martin, are struggling with
not seeing their friends. I have a good friend who follows your work
and knows we are going to speak today,’ the actress said,
who revealed her pal is having a real hard time feeling sexual’ during this time.
Amount – You are required a minimum of 1 video confessional per round.
It allows you to connect HDMI and USB audio and video sources and stream from them to YouTube,
Twitch or Facebook over Wi-Fi or Ethernet.
live cam tube free live porn large nude women best
sex movies 2019
This shit day is finally over. I’m going to relax in a
good bath. What are you doing on the way back?
freeonlineporn pornotube TRX19
Seven women have accused porn star James Deen of violent rape
and sexual assault but his father stands by his side. Thankfully, Aunt Edna won’t
have to share the same digital space with actual porn stars (unless she wants to), although the site will almost certainly have Thanksgiving-themed
XXX action for those who are looking for something spicier than pumpkin pie.
They also have their own app. If you are using an Android device, then you must try this app.
If you want to find new friends, then this site is perfect for
you. Also, it will allow you to find people according to their
countries. They will also find people according to their interests.
For example, you can find people in the USA or India.
This site will help you in connecting with random people.
For ultimate pleasure, you can ask your partner to help you achieve orgasm.
You can even identify your sexual kinks and curiosities
in your dating profile and search for local hotties who
share similar predilections. Hence, you can easily find local people.
The best thing about this site is that you can find people
with similar interests. The challenge is to find a suitable antivirus to protect your system.
Visit my video store for some hot videos and custom requests!
ass horny nudes dm snapchat cumtribute nsfw nude porn show booty sex hot xxx hot
bj amateur webcam sexy cock bbc cum
This is the best I’ve done today, your can visit my website: https://www.serprobot.com/. We finally go forward and face your problems. Hello everyone very warmly.
You really make it seem so easy with your presentation but
I find this matter to be actually something which I think I would never understand.
It seems too complicated and very broad for me.
I am looking forward for your next post, I will try to get the hang of
it!
This is nicely put. !
write essay for money
essays writing service
Hello, after reading this amazing article i am too cheerful to share my know-how here with friends.
Visit my blog: Chelsea Boots
Nude Sex Pics, Sexy Naked Women, Hot Girls Porn
http://neahbay.blazzersporn.hoterika.com/?abigale
animation animal porn do gay guys like regular porn yummy sex and porn gay shit porn peircings porn
trazodone wo prescription
гидра сайт – сайт гидра, hydraruzxpnew4af.onion
A very HappyThanksgiving to all my dear American friends xxx
Thanksgiving2019
Essay solar energy .
Order NOW!!! https://www.google.com.sv/url?q=https://essaypro.me
UYhjhgTDkJHVy
Hmm is anyone else having problems with the pictures on this blog loading?
I’m trying to figure out if its a problem on my end or if it’s
the blog. Any feed-back would be greatly appreciated.
Visit my web-site :: pg slot ทางเข้า
Valuable information. Lucky me I found your website accidentally, and I’m shocked why this
coincidence did not came about in advance! I bookmarked it.
прогон сайта по поисковым системам – регистрация в поисковиках, добавление сайта в каталоги
I blog often and I seriously thank you for
your content. This article has truly peaked my interest.
I am going to book mark your blog and keep checking for new information about
once a week. I opted in for your Feed too.
https://cateringworld.ru/furshet_nabory_moskva
I’m impressed, I have to admit. Rarely do I come across a blog that’s both educative and engaging, and without a doubt, you
have hit the nail on the head. The issue is an issue that not enough folks are speaking intelligently about.
I’m very happy I came across this during my search for something regarding this.
Review my website … เครดิตฟรี
Core competencies resume .
Proceed to Order!!! http://voidstar.com/opml/?url=https://essaypro.co
UYhjhgTDkJHVy
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
kras M40: chattrubate;)
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
An instant, free bitcoin wallet. Receive, store, send bitcoins. Create a bitcoin wallet.
Essay on butterfly effect .
Order NOW!!! http://answers.codelair.com/index.php?qa=user&qa_1=essaypro75
UYhjhgTDkJHVy
When you feel lonely and look for love, UK dating sites help you find
a partner with whom you can chat, gossip, hang out, and share your feelings.
Thankfully several responsible companies have made it their mission to help eradicate the menace of spyware.
First impressions can either help or hurt you:
Facebook works the same way. Hurt and angry, I said yes as
I’d need space to process it. You’ll need 2 – 3 programs to remove spyware from your PC.
Also, there are people of all sorts who
browse the Internet such as sadists, pedophiles, etc. Cyber bullying
is another major concern which children need to
be careful of at all costs. There are gentlemen,
who desire friends not for sexual enjoyment but cerebral contentment.
Apparently, we’re not there to be amazed or entertained, per se, but to get a
job done. All of a sudden you find the permanence break and you keep silence until you get a new topic to start.
Thanks for another excellent post. The place else may anyone get that kind
of info in such an ideal way of writing? I’ve a presentation subsequent week, and
I am on the search for such information.
takipçi satın al
Its very existence was a big step forward for the wrestling industry
as it would help solidify the PPV market as the driving force in making money until The WWE Network
came along. So, instead, we got Yokozuna winning the title
off of Hogan and took on Lex Luger in that awful main event where he
won by countout and celebrated like he won the WWE Title.
Also, we’d like to share our top 3 tips from experienced online dating so you get an idea of what you’d be getting yourself into.
Our Online dating website permits you to get to too many dating profiles for hot single young ladies.
Featuring mobile dating website is a member and without registration 2017, cam online chat online
chat room online dating site, and chat. Even later on, when we became properly famous,
I would find myself pacing in my hotel bathroom after a show,
wondering how best to get rid of the drop-dead gorgeous girl waiting in my room.
https://bit.ly/dunemovie-2021
Please let me know if you’re looking for a writer for your weblog.
You have some really great posts and I feel I would be a
good asset. If you ever want to take some of the load
off, I’d absolutely love to write some content for your blog in exchange for
a link back to mine. Please send me an email if interested.
Cheers!
instagram takipçi satın al
После высказывания В. И. Ленина о том, что «Важнейшим из всех искусств для нас является кино», партийное руководство на местах приняло директиву к исполнению для продвижения киноиндустрии. смотреть фильмы советские на сайте В каждой республике в 1923 году постановлением партии было поручено создание своей национальной киностудии (киностудии появились в Ашхабаде, в Фрунзе, Ташкенте и т. д.)
скачать
Hi mates, how is all, and what you would like to say concerning
this article, in my view its genuinely remarkable designed for me.
Naked girls, snakes and forbidden fruitsdurianemoji Photos do this bandana no justice Come
see it in person this weekend @renegadecraft booth 133.
ONLY 100 made! Use code HAPPYBIRTHDAY for an event…
propecia costs buy propecia – propecia 5 mg for sale
instagram takipçi satın al
Hello very cool blog!! Guy .. Beautiful .. Wonderful ..
I’ll bookmark your site and take the feeds also? I’m satisfied to seek out
numerous helpful information here within the submit, we want work out extra techniques on this regard,
thank you for sharing. . . . . .
Will it be correct that Russian singles can discover enjoy and companionship having an online dating services assistance such as Anonymous Courting For Sexual activity?
Many people are under the impression that Russian single women and men are hard to find, although the opposite applies. http://bbs.weipubao.cn/home.php?mod=space&uid=180503
You will find a high number of individual Russian females and Western guys who have realized enjoy online.
There is also a high number of totally free, Russian courting providers. These free of charge providers are perfect for those single people who want to consider a brand new romantic relationship, but usually do not desire to invest a lot of money doing so.
savethechildren
Police: German chat groups trade child sex abuse …
https://web.sites.google.com/view/nat-carta
https://web.sites.google.com/view/nat-carta
Mail clerk job resume .
Order NOW!!! https://linkvault.win/story.php?title=a-simple-key-for-studybay-unveiled#discuss
UYhjhgTDkJHVy
на сайте
https://web.sites.google.com/view/nat-carta
Provides it your current greatest as well as take pleasure in a new deserving speaking expertise.
Whilst speaking in a very free of charge live video clip
chat room, preserve at heart to be able to look excellent plus really feel
eager. The on the web connectivity is generally
very good, however endures beneath your omission of a 3 grams cable box plus the incredibly inflexible Hardware slot.
Because it’s recently been applied while one element within one particular slot machine, the particular technique has to
control along with one particular storage station. Inturn, the actual technique sounds
is found, but is commonly about an incredibly controlled amount and also
therefore keeps inconspicuously within the qualifications.
In any case, the particular technique efficiency will be adequate with regard to a lot of jobs
and also outshines anything that some other capsules currently have to
present. • MILFs: At AsianCams, MILFs have a category of their own. She’s
one of a group of people in a unique category of quarantine purgatory:
singles living with couples.
smh you don’t know rap my nigga I forgot you da same nigga who thought famous dex
was hot I ain’t arguing wit you !
Final point, please, just be yourself! At some point, she decides to be vulnerable.
Aside from Feeld (previously Thrinder), which
has been widely covered, other top-ranked apps include 3Fun, 3rder, and 3Sum.
In my experience, these apps are often less
intuitive than Feeld, with an ambiguous system of roses, hearts, and likes that
all seem to mean somehow different things and the same thing.
This water-based formula mimics the body’s natural lubrication using odorless ingredients that are carefully selected to preserve the pH of the vagina.
That said, besides its most obvious feature, a good warming lubricant
does more than just add slickness to your body’s most sensitive areas.
Finally, speaking of heat, this pick features a warming agent that adds
a “touch of heat” without being too overpowering for sensitive areas.
If you want more heat, Wicked Sensual delivers in the form of a silicone-based lube.
In the year 2010, homeschooling is gaining more acceptance and
popularity.
Dex poked his head out of the kitchen.
“Stace…good to see ya…you’ve seen Kenobi lately?”
“Sorry to say I haven’t…seemed to disappear again.” Stace smiled.
“I’ll get you that cup of Java, nice and hot then.”
“Thanks Dex.”
“Not a problem, your my favorite Jedi…” He laughs
https://web.sites.google.com/view/nat-carta
Having said that, it is just the small fish from the ocean. That will require having a home, so Fairley told me she applied for the public housing wait lists
in San Francisco and nearby counties. The resort also provides wireless Internet access in public parts.
Today, most of peoples use internet as the first alternative to select and reserve resorts..
Tips To Select and Reserve Online Resort In Bali – Book Resort
Online – Bali Hotels Reservation Service for
Hotels In Bali. This 3.5 star resort also has a
business center with a small meeting room. Bali.If you are travelling in Bali you need
hotel room. Why do you need American’s approval? If it is not why
work with the designer? One particular from the primary
good reasons why most women are looking younger lovers is
due to the fact they want live as a result of adventure.
Youthful adult males are attracted for the strategy to meet
with mature girls.
This design is steller! You obviously know how to keep a reader amused.
Between your wit and your videos, I was almost moved to start my own blog (well,
almost…HaHa!) Fantastic job. I really enjoyed what you had to say,
and more than that, how you presented it. Too cool!
@MicaSuarez12 miras los chats de omegle porq no tengo camara 🙁
They are making you feel as though the germs that every child
comes into contact with every day are somehow irrefutable proof of your
substandard morality. See, I’m a professional, when it comes to
finding the best, famous, and most popular places
on the internet for (free) live cam sex. “You do have to kind of trust the community and hope people are putting it out there,” says
Evelyn (a pseudonym), a 37-year-old nonprofit professional, who attended the NSFW couples’ night.
He’s an adult. Let’s hope he’s willing to make any effort whatsoever to stay in your
home. The agreement when he came back to my house was that this was the
last stop, and he had to be focused on school in order to
stay. This fantastic and extremely reliable online portal will enable
you to find cheap chat lines in order to indulge in fetish phone sex and cheap teen sex chat.
https://web.sites.google.com/view/nat-carta
sildenafil davis pdf pfizer viagra viagra 100mg price
free teen lesbo lust top 100 female porn stars naked black men blogs adult xxx vidoes movieclips
teenagers
omegle en modo “cha>” NO con lg>cámag>!
https://web.sites.google.com/view/nat-carta
free reality sex videos sex chatrooms free big boobs tites best mature cams
where to get accutane uk – buy 40mg accutane online accutane purchase uk
Finally focus cam やんちゃBOY やんちゃGIRL of my favorite
boy can be watch on youtube
Let’s streaming
北川玲叶
En iyi takipçi hilesi sitesi ile instagram takipçi
hilesi yaparak
ücretsiz olarak her gün instagram takipçi hilesi
kasabilirsiniz :
takipçi hilesi kasabilmek için hemen aşağıdaki linkten beğeni yada
takipçi hilesi için siteye gidebilirsiniz
https://bit.do/heytakip
https://web.sites.google.com/view/nat-carta
I think NSP and TWRP could rock it and other holiday songs to the next level.
But some NSP Hanukkah/general holiday songs would be amazing.
Wait so like do you want an NSP Under The Covers CHristmas Album where they perform hits
like Last Christmas, All I want for Christmas, etc. or an NSP Original Christmas Album where Danny
Sexbang and Ninja Brian get into the holidays with
their usual sexy ninjitsu shenanigans? 2019 was the 10 year anniversary
of comedy band Ninja Sex Party, so now there’s a Kickstarter to help make a tribute album for the band!
They compare it to used tape, worn out shoes, empty toothpaste tubes and
now apparently chocolate. One is now designated
for COVID-positive and COVID-suspected patients, complete with its own operating room.
So far it’s been really good, my school is much
better and my grades are up, the house and area are
really nice, except for one problem- my brother
and his husband are really really loud in bed. So in the event that your focal zone are the genitals, breasts and pubis, the massage takes
the form of orgasm through masturbation or sex itself.
Reading her book Tantric Orgasm for Women has changed my life forever.
cialis 20 mg price costco evolution peptides tadalafil cialis tadalafil
That’s good why there’s a stigma around girls watching porn or having
sex is crazy
Checked some of y’all sex facts & the report came back is that y’all not even like
that hate to hear It!!
Emerging market analyst resume .
Proceed to Order!!! https://gameduaxe.info/forum/profile.php?section=personality&id=554130
UYhjhgTDkJHVy
small breasts free live nude virtual reality sexy nude women with large tits
Last night was my final book event of 2019 and probably the most fun – talking about sex for an hour or so
with these four amazing women. Thanks to the @feministbooksoc @Rosie_B_T for asking
me and everyone who came along …
Other teammates cannot adjourn to these people and
that’s the main thing. Young people are unwilling to turn to adults for help due to
fear of being judged. These are the things
you’ve looked up to since you were 12 years old,” says Valentine. Valentine was pleased with that image, in which the band came across as “fierce and empowered.” But she only recently realized that that cover also boasted a sexual double-entendre headline: “Women on Top.” Says Valentine incredulously, “I
just looked at it today! The fascinating content ranges from a peep inside Captain Scott’s Hut in Antarctica
to a journey round Europe with Impressionist painter Claude Monet, in which his works now hanging in London’s National
Gallery are paired with the scene today. ” have resounded since their breakthrough album, Dookie, sold in similar quantities in 1994 – when the group decide to floor it, there are few who can touch them. As it turned out, Rob Cavallo’s figures were wrong; by the time the cash registers had stopped ringing up copies of Green Day’s latest album, the Oakland trio’s one true masterpiece, American Idiot had sold more than fourteen million copies. The man must consume zinc supplements in order to gain strength and produce more sperms.
betandyou букмекерская контора онлайн
I blog quite often and I seriously thank you for your information. This great article has truly peaked my interest.
I am going to take a note of your blog and keep
checking for new details about once per week.
I opted in for your RSS feed as well.
Maybe Steinbeck a little bit. “Before the tech existed we’d set up two cameras, one pointed at the video game screen and the other at us, and we’d feed it into these two little boxes to make it work,” recalls Evans.
Once we were all gathered in the back, seated on overturned milk crates, my
boss removed a folded-up piece of paper from his pocket and began to read a letter from our company’s management that thanked us,
presumptively, for our “confidence and steadiness” and offered
our store a bonus. I got a lot of blowback on that, and I wrote a piece
in The Washington Post trying to explain my position more
fully, and after that I got left alone. Just days
away from the hearing, he got a surprising late-night
call. There are days when I think this is all a dream.
There is, however, already ample and easily available evidence that much of Deborah Feldman’s depiction of Hasidic life is fictional, much of it coming from friends
in the ex-Hasidic community.
http://humanz.mn/i/1685
Labour can now only pray that Brexit turns out to
be a disaster for Britain. Meanwhile, good news for parents:
Amazon is now offering a bunch of Sesame Street e-books for free.
However, very few of them offer their services for free and very few of them
have thousands of users online at any given moment. Your experience on Whitehousecams is free and will do wonders to your body and mind and
fulfil your sex cravings. Yes that’s right. You lose body fat, get a small,
lean, tight, toned body that looks good in and out of clothes.
Double Take – Some of the cams aren’t very easy to see because
the video quality is about as good as girl in it.
It takes us down the gravelly, pothole-filled road of video games and relationships.
All profiles are real girls, skype names of girls and phone numbers are
also checked by our moderators, communicate only with real girls.
His belated admissions of love followed by blame and outrage are just a convenient
way for him to end the affair and justify doing and continue to tell himself what a great guy he is.
It’s a wrong notion that only men have fantasies and women are like angels.
THAT WAY WOMEN LOVE TO WEAR A GIRDLES AND SHOW THEM OFF AND THE SEXUAL
ATTRACTION OF THE GIRDLE TO OTHER PERSON WOMEN AND MEN.
IT’S ROMANTIC AND SEXY TO BE IN A GIRDLE. I AM NOT MARRIED NOW BUT HAVE OTHER WOMEN THAT LIKE ME IN MY BRAS GIRDLE.
AT THIS TIME I AM NOT MARRIED TO ANY ONE BUT WHEN I WAS
MY WIFE THOUGHT I WAS WEARING A GIRDLE JUST TO BE SEXY
IN THEM AS A WOMEN IS IN THE GIRDLE. A longtime
fan of the band Pearl Jam, Rodman attended one of their gigs
in Dallas in 1998 before taking to the stage himself topless and with no shoes on while
‘swinging a bottle of wine around’. If a
male model is looking to advance their career while living the lifestyle that they
dream of before their modelling career reaches that point if it ever does why wouldn’t they turn their good looks and sex appeal to escorting as
a way of living well in the city where money counts for so much?
Do yourself a favor do not lie! The odds are finally in your favor when looking for a date.
Young guys will be looking for sexy and smart girls for love,
romance or for developing relationship for long terms. In the
past, a physical relationship between a man and woman was an important aspect in developing relationships.
Grindr has a well-earned reputation as a hookup app, and millions of singles have used the app to get
laid, find dates, and build relationships on the fly.
The young generation might be looking for partners in order to maintain friendship,
love, romance, or any other type of relationships. First, you must define what you are looking for – whether it is Christian singles, adult dating, gay dating, Canadian singles or whatever.
They are a must for people who are looking for partners for
any purpose – marriage, chat bodies or even a one night stand.
Topics for essay writing .
Proceed to Order!!! https://www.wattpad.com/user/bargeflare53
UYhjhgTDkJHVy
Nice bro thank you.
https://haraj-alarab.com/products-1548477098302
Magnificent beat ! I would like to apprentice whilst
you amend your website, how could i subscribe for a blog site?
The account helped me a appropriate deal.
I had been tiny bit familiar of this your broadcast offered shiny transparent concept
ABSURDO! JORNALISTA SUGERE QUE MIN. DAMARES DEVEREIA TER
FEITO SEX… COM JESUS CRISTO! …
Last night was my final book event of 2019 and probably the most fun – talking about sex for an hour or so with these four amazing women. Thanks to
the @feministbooksoc @Rosie_B_T for asking me
and everyone who came along …
2662
https://movingcompanies.pro/moving-company-tempe-az.html
I’m live on webcam now! Come & join me! xx
Savage has not publicly specified in which state these alleged incidents
took place, and it’s unclear whether or not she has taken her accusations to police or legal counsel.
Phillip Garrido hoped to schedule an event for his religious group
“God’s Desire.” He spoke to campus police official Lisa Campbell, who
focused on more than his request. Of course without tone of voice or detecting sarcasm, people can come off more polite then they would be
I a face to face conversation. Nonetheless, girls sex dating near me can switch things up and you may get to know new
practices and places that the other couple likes,
and in this way bring those later on into your , making your sex life substantially more fascinating.
Fixing your hookup on Free Sex Match, have confidence
all the way toward taking you from the dating stage to some attractive woman’s room is absolutely simple, fast and completely free.
free backlinks
Интернет-магазин продает дизайнерскую мебель личного производства по привлекательным ценам. Если не хотите приобретать стандартные мебельные гарнитуры, а желаете выбрать модели определенного стиля, которые будут гармонично сочетаться и станут украшением любого помещения, тогда загляните в каталог онлайн-магазина.
Вы можете подобрать мебель:
· для гостиной,
· столовой,
· спальни,
· прихожей,
· кабинета.
Мебель бренда авторского исполнения изготавливается в различных стилях. Покупатели смогут выбрать дизайнерские мебельные комплекты для комнат, выполненных в классическом, скандинавском стиле, провансе, арт-деко, модерне, минимализме.
Помимо столов, стульев, шкафов, консолей и иной мебели на сайте фирмы «Эксив» вы можете выбрать дизайнерские предметы декора, которые дополнят интерьер и дадут помещению индивидуальность. Зеркала, люстры, торшеры, бра, светильники можно подобрать для каждой комнаты, прихожей, лоджии, террасы, напольные зеркала https://farming-mods.com/.
Предметы мебели делаются из натуральных по максимуму материалов с высококачественной фирменной фурнитурой. Для обивки мягкой мебели используются: велюр, натуральная и экокожа, рогожка, нубук, микровельвет, шенил. Каркас изготавливается из массива дерева.
Как сделать заказа в онлайн-магазине бренда Exiv
В перечне вы можете выбрать готовые изделия и заказать изготовление мебели нужной вам конфигурации по личным размерам. При этом у вас будет возможность кроме этого подобрать цвет материала отделки.
Окончательная цена выбранной вами мебели, изготовленной на заказ, будет зависеть от материала и размеров. Для того чтобы уточнить цену, позвоните менеджеру по телефонам, обозначенным на сайте. По заказу мебель изготавливается в среднем в течение 2-3 недель. Кроме этого вы можете забронировать на 5 дней понравившиеся предметы, которые будут отложены специально для вас до оплаты.
Заказать товары в организации «Эксив» вы можете с доставкой по Москве, Подмосковью и отправкой транспортными компаниями во все регионы Рф. Цена доставки по Москве – 1000 р. Для того чтобы узнать стоимость доставки в другие города, позвоните консультанту либо задайте вопрос в форме обратной связи.
Оплата возможна курьеру при получении заказа наличными или банковской картой. Кроме этого вы можете оплатить товар на веб-сайте либо по безналичному расчету. Если заказ отправляется в регионы, требуется полная предоплата.
tiktok takipçi satın al
As well as the money-making imperative, this audience interaction is presumably
there to defray Dessau’s deafening silence: if you can’t hear them laugh,
at least – by talking with them – you can remind yourself,
and anyone looking on, that there is an audience
there. Now, ask yourself, if that is how you see yourself as feeling your
best and the most attractive, and even if the opposite sex might not think of you as that “God’s special gift” that was created just for them,
are you going to feel comfortable going what may be outside your comfort zone.
I sitting straight down beside the girl and also said the particular suavest, nearly
all superior thing I can think of. When they meet in the middle, glide one
finger up over the crack of his bum while simultaneously drawing the other down between his thighs.
Give one to your partner as a gift on special occasions.
Be honest with your partner.
Hmm it looks like your site ate my first comment (it was extremely
long) so I guess I’ll just sum it up what I wrote and say, I’m thoroughly enjoying your blog.
I as well am an aspiring blog writer but I’m still new
to everything. Do you have any tips and hints for beginner blog writers?
I’d definitely appreciate it.
Finally focus cam やんちゃBOY やんちゃGIRL of my favorite boy can be watch on youtube
Let’s streaming
北川玲叶
you’re in reality a excellent webmaster. The web site loading pace is amazing.
It kind of feels that you’re doing any distinctive trick.
Moreover, The contents are masterpiece. you have performed a great job
in this subject!
Полезная продленка – это продленка для учеников 1-6 классов, которая не только решает обычные задачи (выполнение домашнего задания и присмотр за детьми), но и организует гармоничное развитие детей, создает условия для оптимального восстановления после учебного дня, обеспечивает интересный и увлекательный досуг.
http://asmechta.ru/foto-video/ Посещение занятий балетом, позволяет достичь успеха во многих сферах жизни, таких как здоровье, красота, образование, культура.
Преподаватели нашей студии используют систему Московской Академии Балета (2003 г.), адаптированную под возраст детей 4 и старше лет. В разных возрастных группах проводятся уроки классического танца, партерной гимнастики, растяжки, разучиваются танцевальные движения.
instagram takipçi satın al
Have you ever considered publishing an ebook or guest authoring
on other websites? I have a blog based upon on the same
information you discuss and would love to have you share
some stories/information. I know my readers would appreciate your work.
If you are even remotely interested, feel free
to shoot me an email.
Stop by my webpage :: เครดิตฟรี
Голосуй за меня или жми СПАМ. Пусть решает судьба.
https://www.instagram.com/vuhinojulebino/
instagram takipçi satın al
Sushmita’s eyes flew wide available as her orgasm rushed through
her body. Sushmita’s eyes fired wide open as she felt
the initial burning ache in her ass and her breath started to follow in other words jeans.
Sushmita discovered the preliminary burning sensation had
gone to be actually switched out with a feeling of volume that she had
certainly never experienced before. My better half must have obtained familiar with
the sensation of his cock hammering into her butt, as she wheezed out,
“I am actually mosting likely to orgasm, Vicky! She should possess been actually around the grow older of 50 after that. But coming from after that on, I liked this tip of snagging my cock and having an orgasm the white fluid coming from it.’s max well to certainly not let my cock out. But in some way I felt it tough to remove her away from my thoughts as well as every time I considered her, I would like to possess her. I went inside the commode and also came out promptly and as I was actually passing the kitchen space I discovered that she was only set down as well as not resting.
veuillez cliquer sur le prochain post – veuillez cliquer pour la source, ou trouver du viagra professional
Обучение в Чехии – гарантированное поступление в колледжи Чехии для русскоязычных выпускников 9 классов. Набор открыт – скидка 600 евро, записывайтесь!
Чехия колледжи для русских
Обучение в Чехии – гарантированное поступление в колледжи Чехии для русскоязычных выпускников 9 классов. Набор открыт – скидка 600 евро, записывайтесь!
Колледжи Чехии после 9
Medication information. What side effects can this medication cause?
pregabalin pills in Canada
All information about medicines. Get information here.
Дебетовая карта Tinkoff Black
Зарабатывайте деньги, а не бонусы. Закажите дебетовую карту и получайте кэшбэк с любых покупок
Бесплатно
Обслуживание карты — 0
Кэшбэк до 15%
В трех выбранных вами категориях
До 6% годовых
Начисление процентов ежемесячно
Главное для нас результат! Поэтому формируем малочисленные группы, 6-8 человек, что позволяет обеспечить индивидуальный подход к каждому клиенту. Занятия ведут только квалифицированные педагоги.
http://asmechta.ru/glavnaya/prodlenka/ Посещение занятий балетом, позволяет достичь успеха во многих сферах жизни, таких как здоровье, красота, образование, культура.
instagram takipçi satın al
Its not my first time to go to see this web page, i am visiting this web site dailly and obtain good data from here daily.
I am hoping this is an easy question. Remind this to yourself
if you are faced with the question ‘So how many women have you been with in the past?
Also men in suits (men in black) where then norm for that generation so they are STUCK in the past also the War generation the same but they like a man in a uniform.
SO MY POINT IS THIS THING IS KINDA PUSHING WOMEN AWAY
FROM MEN. I’m disappointed that you commented that perhaps
women get paid less because we have lighter work.
The women seem to actually be better educated and in my opinion better motivated work wise than the men (In Saudi Arabia women are schooled
separately to the men). Your article is a real eye opener; I never thought that
alcohol, drugs or prostitution even existed on the soil of Saudi Arabia.
That means those that honor and respect truth, honor and respect Him; and
without even ever knowing His name or His story, accept Him.
I even turned cookies off.
Medication information sheet. Generic Name.
lisinopril without insurance in US
Actual about medicine. Get here.
Рейтинг дистанционных онлайн курсов – РєСѓСЂСЃС‹ b2b маркетинг
для получения образования и профессии для начинающих специалистов – бесплатные и платные, повышение квалификации и переподготовка
buy propecia 1 mg online safely
Meds information sheet. What side effects?
generic lyrica without a prescription in US
Actual news about medicine. Read information now.
Hello! I’ve been following your site for a while now and finally got the
courage to go ahead and give you a shout out from
Huffman Texas! Just wanted to mention keep up the fantastic work!
Kamagra Barcelona
While Chuck is supportive now, she admits that he took some time to
get to grips with her adult film work, something that she says was due in part to
his southern background, noting that there is ‘still so much shame around it’ in the South.
However, she has since removed her clips because she wants to obtain her Tennessee adult entertainment permit
before sharing any more content. I know there is much more to
your story that you are not sharing here. Judith Douglas, thank you for sharing your experience.
The roommates before seeing Mike wrote down a bunch of
questions for him about his prison experience. The psychic also talked
to Deena about her late father John and said he was proud of
her and held her baby CJ before sending him down to her.
What I am really trying to say is, don’t get hooked into
the opinion that the guy is always at fault for
getting the child underway, started in the womb.
I am very happy to find your blog, I feel 100% identified
with everything you say I’ll keep reading you !
When I initially commented I appear to have clicked the -Notify me when new comments are added- checkbox and from
now on whenever a comment is added I recieve four emails with the same comment.
Is there a means you can remove me from that service?
Thank you!
Рейтинг дистанционных онлайн курсов – Mylj
для получения образования и профессии для начинающих специалистов – бесплатные и платные, повышение квалификации и переподготовка
jajaja se acuerdan de omegle? cada chat era: viejo pajeandose, persona que ves por 1 segundo y corta, camara en negro, viejo pajeandose,
grupo de amigos, viejo pajeandose
Hey there! I just wanted to ask if you ever have
any trouble with hackers? My last blog (wordpress) was hacked and
I ended up losing several weeks of hard work due to no backup.
Do you have any solutions to protect against hackers?
she’s a webcam model and they go by popularity on those sites.
Attractive element of content. I simply stumbled
upon your weblog and in accession capital to claim that I acquire actually loved account your blog posts.
Any way I’ll be subscribing for your feeds and even I achievement you access persistently rapidly.
Look into my blog :: เครดิตฟรี
To correct this, one can go in for vascular reconstructive surgery which can help to increase the blood flow towards the genital organ thus helping the
person to sustain erection. The insulin resistance and high cholesterol associated with excess weight can hinder blood flow to your sexual organs.
Dickey was arrested and search warrants were served on residencies associated with
him. We should use our freedom and liberty not selfishly,
but in consideration of the people around us.
I write now not just to promote social media use but also self-expression. I believe the Social Network revolution of our time marks a reason – to
carter for our social needs that seem to evade us.
What is the reason for the emptiness you feel? Women know how unnerving and icky it feels when a person ogles, touches,
cops a feel or makes in-appropriate or unwanted sexual comments.
Some of us are driven by jealousy and would not even know.
I am curious to find out what blog platform you’re working with?
I’m having some minor security issues with my latest site and I’d like to find something more
safe. Do you have any recommendations?
Here is my homepage whatsapp (Fawn)
Напишите необходимые 200 решений, если вы завтра станете президентом, определите их на группы по 10 штук и расположите в последовательном порядке принятия . Создай свои Проекты будущего
Every fucking time it’s he who gets all the attention, not a pornstar.
It’s not really a top 10 of less-known mature pornstars, instead, it’s all about the all-time
greatest and Jayden Jaymes as the VIP of MILF pornstars.
Do you know the difference between the hottest granny and the ugliest MILF?
She rocks the typical MILF look: bleached blond hair, impressive
fake tits, and the hottest apparel. Catching MILFs at their earliest is great as you have an opportunity
to see their careers go from entry MILF stage
to professional GILF. Here’s an example of a MILF pornstar
that is on the edge (currently 46-year old).
She is now 45 years old and has many fans. Now at
48, the American female actress benefited from Lisa Ann’s fame,
as having same last nickname helped her tremendously. But now newer games may be comes only designed for individuals and that’s the sexual intercourse applications.
Are you looking through how to zest up wedded couples existence with grown-up games
to have a fabulous time and experience. Next thing we need to do
is get Van to stream on chaturbate, that would be the ultimate experience.
Its not my first time to pay a visit this web
site, i am visiting this website dailly and get nice information from here
all the time.
I will be filing an official complaint for slander and defamation. For additional information or queries please contact my lawyer Xxx
I just use a webcam, but then I don’t really do chatting streams so it’s
not as big of a deal for me.
Though I’d think if you had a capture card and a HDMI cable you could mirror your camera that way probably?
Assume it would depend on the camera.
XXX SEX VIDEO HDToday, something is working,
and colleagues looking at my neckline… tensed, and I will be horny.
محارم سكسٌٍٍِِ 3773JUCS …
His decoys, Blas says, are stay-at-home
moms, spread out across several states. He has a
team of decoys, adult women who pretend to be minors. For those of you who need a dedicated IP,
you can get one from the company, but you’ll need to contact support to get help setting
it up. Taylor took jobs at fast-food joints to support her daughter, a
burgeoning artist. Taylor flipped to the next page. Sophia Gabrielle Chery is 29, and follows “POPSquad Prey on Predators,” a
page with 22,000 likes on Facebook, which operates, among other
states, in Connecticut, where she lives. With smartphones and the Facebook app at their fingertips, people can check in with the page at
any time of day. Check with the sex shops online to find out which
sex toys would best suit your needs; they come in various shapes and sizes.
The site also incorporates the use of hashtags, which makes it super easy for viewers to find exactly what they’re looking for.
That’s encouraging. Still, it might not be a horrible idea to have an antivirus app around.
15 best antivirus apps and best anti-malware apps for Android!
GetJar is a mobile app store that hasn’t always had the best rap but it does have some pretty decent porn apps and porn games.
It’s probably the best app store specifically for porn apps and porn games.
With such a large library of content, you’d expect the app to be pretty decent.
The selection is quite large and includes apps, games, and even big name
apps such as the official Pornhub, RedTube, YouPorn, and Porn Tube apps.
Currently, there seems to be dozens of porn and sex themed apps and games, including games
like Sexy Space Invaders, the official YouPorn app, and even some sex-oriented
education such as masturbation techniques. It represents a collection of porn websites that
range from RedTube to Tube8 and even YouPorn.
How does it know the biometrics are secure? There are lots of cougar dating sites
in the world. They all give you the chance to meet hundreds of adults
from around the world who are online 24 hours a day!
Younger men are fun to date and are a better option for cougars that need
to try diversity in their dating life. The site is quite easy to navigate, and while
the webcam quality could be better in some cases, the
community and girlfriend experience is what really
sells MFC. However, if you prefer cam to cam chat,
turn on your webcam and start chatting! Most of the shows are done in free chat, once the model has reached
the token amount to start their performance. To millionaires, spending
does not disturb them so long as they are seeing where or what their money is doing.
This strange happening occurred during the first part of last November 2018.
I was spending long hours on my page with the hopes to build up some extra
money for the upcoming Holidays. They were one of the first to fund us at the beginning, and still cover all our travel and show costs.
Girls on latex, dominatrix, masters, models that are in bondage, foot fetish everything is possible here and do not forget this is all
free with not any additional cost! You may find an Intel Celeron M or a VIA processor in first-generation models like the ASUS EeePC 4G plus
the HP 2133 Mini-Note, but you’re better off skipping
these. A guy can be the most perfect Adonis, but it would be no surprise if the
girls will run away from him like a dreaded disease if he is as clean as
street wino. Many netbooks will run fine on 1GB of memory, and most can be
upgraded to 2GB, provided you may earn this straightforward addition yourself.
Non-Hindus may not enter, which prevented my taking photographs
inside. In penance he started the practice of venerating a young
virgin as a living goddess. I’ve never seen a real live goddess.
One could spend days wandering Bhaktapur’s narrow back streets and quaint alleyways discovering small market squares carpeted with clay pottery bowls baking in the
sun or stacks of hand-hammered brass milk cans
piled high.
hydra onion – ссылки на гидру онион, актуальная ссылка на гидру
Новый метод Email рассылок https://www.youtube.com/watch?v=TJsiM7wDGLw
pron free live nude chat online adult chat women with nice boobs
Times have changed over the last 23 years. Big tit amateur
nudes explore their sexuality with massive cocks like it’s
their last day on earth! Video of the day! Every day
discover online sexy videos, anal sex videos, hardcore xxx videos, sexy pornstar movies,
fucked baby videos, nude celebrities, hot porno sex tapes,
asian xxx videos, pussy and teen fuck films, mom, ebony, black
and indian blue sex videos online. Sunny Leone is without doubt the Hottest Indian Porn Star we
have seen. If yes, then these Indian girls numbers will help you to
contact them on Whatsapp. This unconditional acceptance by a crush and the
peer interaction that comes with it can sometimes cause young girls to say that they “love” the
celebrity. I love him and want to be his wife.
Our app is very safe to use and it is like a playground
for adult people that want to spice up their sex lives.
Saved as a favorite, I love your website!
зайти на гидру с телефона – зеркало на гидру тор ссылка, ссылка на гидра
Really, you’re going to carry this stuff from the ’50s on with
you? So if you’re ready to tackle new things and experiences, or if you’ve
not had much luck with the opposite sex, then why not try online dating?
Why? Who the fuck cares? Viewers of the Iowa nest recently saw an eaglet who was accidentally knocked off the nest.
The birds typically mate for life and use the same nest year after year to raise their young.
Plus, the idea is to establish a baseline comfort that the person you’re
talking to isn’t a danger, not to dig up conversational ammo so you can pretend to like
the same bands. Phone calls and emails aren’t always enough either, especially since neither method allows you to see the other person in the flesh.
All you need is a webcam and an internet connection to make money with this method.
риобет промокод – бонус 1xgames, промокод риобет
I’d like to thank you for the efforts you have put in penning this site.
I am hoping to view the same high-grade blog posts
by you in the future as well. In truth, your creative writing abilities has inspired me to get my own blog now
😉
My homepage nama free fire keren
Данный вид скола похож на глаз быка и получил название”бычий глаз”. Несмотря на свое грозное название он не так опасен для стекла, т.к не имеет направленных лучей. Лечится несложно и после ремонта практически не заметен.
https://autosteklo77.com/katalog-avtostekol/folder/lobovoye-192 Всё будет зависить от степени повреждения. Повреждение внутренних полостей заполняется специальным составом, имеющие такой же коэффициент преломления, как и стекло. После полимеризации внутренних трещин под лучами ультрафиолета поверхности надежно склеиваются. Ремонт лобового стекла предотвращает дальнейшее развитие трещины. После ремонта дефект стекла остается практически не заметным.
Want to know what happens in these chatrooms, log in to find out!
I don’t find the need to spend hundreds of dollars on studio-grade lighting for my
shows. Remember if you test positive unless you are very
ill you will just be confined to your house so no rush to be tested we just need the information. While my clinic is ok
not all of them are. While there is no “girls only” button and no way for people to indicate their genders unless stating it
right away in the chat, it shouldn’t discourage you from using the site.
Also he told me while we were laying there after I pretended to get
myself off (sad I know) that laziness is a turn off and that
living with me has been a difficult adjustment because he
likes to work out and eat healthy (which I normally do)
but i haven’t been, and it is difficult for him because if we are
living together we should be on the same page.
вход на гидру онион – гидра онион официальная ссылка, union гидра сайт
Forgot about Paris Hilton and Kardashian, but they were still celebrities before
that, they have money and support. After a while I turned around to him and said, “You clearly don’t have the money for this. I think you maybe have a problem.” He’d come online most days.
Come on in and enjoy hardcore scenes with straight couples, gays guys, lesbians,
barely legal teens and grannies involved. These teens on cam are human beings and respectively have feelings.
So get your socks up for all the adrenaline rush you are going to experience
through our live football streams. Digital sexual commerce,
by its online nature, can feel distancing, helping to create an illusion for sex workers that their experience is unusual when, in fact, this is a shared experience they can find solidarity
in. These babes know that providing you with a rewarding
experience is not only about pleasuring you, but also about making
sure their audio is clear and their webcam sharp and in high definition.
You can choose one model and go live video chat for free –
We have the best adult cams girls on the internet. Do you feel like you’ve
watched all the porn on the Internet and you’re fed up with all those silly porn tropes?
Cassidy is a newcomer to the porn scene, but her career has started with
a bang and you only need to take one look at her to find out why.
If you are tired of guessing where to meet a woman who can easily fit in your sexual life you can look there.
There are popular and sexy models of all ages who are offering you both shows and
virtual sex. Models are into experiments with their bodies which include not only the thing with the dildo and the pussy or mouth or even ass.
We have camgirls to suit every taste and they are available 24 hours a day for your
enjoyment.
ссылка на гидру в тор браузер – ссылка на гидру тор, правильная ссылка на hydra
Macrobid Where Can I Buy In Internet Doncaster
ссылки зеркала гидры – ссылка на гидру зеркало, гидра онион официальная ссылка
If you would like to improve your familiarity simply keep
visiting this site and be updated with the newest news posted here.
Покупаете первый автомобиль или хотите обменять свою старенькую машину на что-то поновее – в AVALON рады всем!
http://avaloncars.ru Мы выстроили процесс для комфортного обслуживания клиентов.
Удобный график работы, профессиональная работа менеджеров, выгодные условия продажи автомобилей с пробегом – все сделано для того, чтобы вы остались довольны посещением AVALON и рекомендовали нас друзьям и родственникам.
ссылка гидра анион – tor ссылки гидра, гидра онион сайт ссылка
http://polesietour.by/index.php?subaction=userinfo&user=akagyv
ссылка на сайт гидра в тор браузере – union гидра сайт, ссылка на официальный сайт гидра
bloody макрос – скачать макросы на калаш раст, макросы на раст бесплатно
вход на гидру онион – hydra union ссылка тор, официальный сайт гидра онион ссылка
гидра онион официальная ссылка – сайт гидра на торе ссылка, гидра онион сайт ссылка
first touch mobile os kombi przytul mnie wrzuta er pacote de musicas eletronicas de toquio mastichor serial in er one piece episode 540
https://kavelik333.com william young and sons transit for sale hi platinum full crack internet mujhe rang de mp4 video fresh top 40 1 decembrie 2012 gmc rst gila mountain bike forks
ps i love you novel ebook 101 vultures alex winston games xbox emulator for pc cover album 112 anywhere lange afstand relatie liedjes en
Hi friеnds, іts great post on the toppic of tutoringаnd fully defined, keep iit up all the time.
my blοg: 日本 淘宝
I’m not sure why but this blog is loading very slow for me.
Is anyone else having this issue or is it a issue
on my end? I’ll check back later on and see if the problem
still exists.
Crowe first bought land at Nana Glen in 1999 before later expanding his property to
include nine surrounding lots. Crowe first bought land in Nana Glen in 1999 before later expanding
his property to included nine surrounding lots.
The service just made the first Harry Potter book
available as well. Young Girls First Videos34.
Young Candid Teens48. Top 100 Young Model49. Our radically low prices, fast
technical support and top notch network is key
to your success. DISH Network offers four program packages.
Another friend lives in a remote part of Washington State and the tiny town he lives near only got a decent broadband service about
four years ago. A friend dropped everything to come over and let her cry into
his shoulder for five minutes. Watching my friend in rural Washington discover what he had been missing in dialup internet land all those years was actually very funny.
All models were 18 years of age or older at the time of depiction. Is there even a point to making media with ‘fanservice elements’ in them anymore in the age of the internet, where
if someone wants their waifu in a sexy outfit, or to see a pair of unclothed breasts or ass
cheeks it’s simply a google search or a forty dollar porn commission away?
she’s a webcam model and they go by popularity on those sites.
Перед поступлением ТС в салон, мы тщательно отбираем автомобили, проводим техническую и юридическую проверку, а также предпродажную подготовку.
https://avaloncars.ru/trade-in Trade-In в салоне автомобилей с пробегом AVALON, позволит вам сэкономить время, и сразу уехать на новом автомобиле.
Hey are using WordPress for your blog platform? I’m new
to the blog world but I’m trying to get started and set up
my own. Do you require any coding knowledge to make your own blog?
Any help would be really appreciated!
I love it when folks get together and share views. Great website,
stick with it!
visit site pin up casinopin up casino
Сео академия
Hello, i think that i saw you visited my site thus
i came to “return the favor”.I’m trying to find things to improve my
site!I suppose its ok to use a few of your ideas!!
1xbet букмекерская контора
Let’s not forget male porn stars may not get paid as much but the top guys do about 300 paid scenes
a year & on average career last 7 years.
They are more also more likely to get directing jobs too.
How many female porn stars even shooting
100 paid scenes a year?
Одно из главных преимуществ компании – собственное производство на территории Московской области, общей площадью 1460 квадратных метров. Там расположены: участок механической обработки, участок покраски, сборочный цех и отдел технического контроля.
https://aviaproduct.ru/airfields/aerodromnaya-tormoznaya-telezhka-att-vpp/ компания «АВИПРОДУКТ» самостоятельно производит и успешно поставляет оптические линейки «ОЛ-1», предназначенные для точного определения толщины слоя осадков на искусственных покрытиях аэродромов.
Looking For Sildenafil
This article provides clear idea designed for the new viewers of blogging, that genuinely how to do blogging and site-building.
Hi there! I understand this is somewhat off-topic however I had to ask.
Does managing a well-established blog like yours
take a large amount of work? I am brand new to writing a blog but I
do write in my diary everyday. I’d like to start a blog so I can easily share my personal experience
and feelings online. Please let me know if you have any kind of ideas or tips for new aspiring blog owners.
Thankyou!
Goߋd day! This is mү first visit to your bloց! We are a collection of volunteers and startіng a new prpject
in a community in theе same nicһe. Your blog provided us valuablle informnation too worк on. You have done a wonderful job!
Hello would you mind letting me know which hosting company
you’re using? I’ve loaded your blog in 3 completely different web browsers and I must say this blog
loads a lot faster then most. Can you recommend a good
internet hosting provider at a reasonable price?
Kudos, I appreciate it!
Feel free to visit my web page; สล็อตเว็บตรง แตกง่าย
Easy MP3 Joiner is just the piece of software program you could have been searching for! Overall, Free MP3 Cutter Joiner is primary on functionality and has a very previous wanting interface. The application solely supports MP3 recordsdata and the dearth [url]https://www.mp3joiner.org[/url] of options lets this utility down. If you need to work with MP3s and no other formats, and want only fundamental performance, Free MP3 Cutter Joiner shall be ok to your wants.
This free MP3 cutter and MP3 joiner helps a large amount of enter formats including MP3, WMA, WAV, AAC, FLAC, OGG, APE, AC3, AIFF, MP2, M4A, CDA, VOX, RA, RAM, TTA and rather more as source codecs. Any audio information will be lower or joined to the most well-liked audio codecs.
Weeny Free Audio Cutter can join multiple audio files in addition to split them into components. The MP3 Merger supports MP3, OGG, WMA and WAV files. What’s extra, this system has a constructed-in audio editor, which allows you to set the sampling frequency, channel mode and audio bitrate.
This software give you full help for Join Audio files too quick. Merge or Be a part of two Mp3 information collectively. You [url]https://www.mp3joiner.org[/url] can specify the output format of the outcome and likewise other output settings such quality, bitrate, sample fee, channels, bits per pattern, CBR, VBR, VBR high quality e.t.c.
This small instrument is nice in its simplicity. Joins MP3 and WAV information, does not convert MP3 to WAV and again, like others. This software is much like the MP3 Cutter Joiner. As the identify implies, it will probably do each. Also, this software stands out with its output high quality.
Tips: Faasoft Audio Joiner permits to rearrange file order before merging if needed. MP3 Joiner is a lightweight utility that serves one main function, particularly that of merging your MP3 recordsdata, with very little consumer input being required within the process.
It has the flexibility to join virtually all audio codecs resembling MP3, WMA, WAV, AAC, FLAC, OGG, APE, AC3, AIFF, MP2, M4A, CDA, VOX, RA, RAM, TTA and lots of more to MP3, WMA, WAV and OGG. On the identical time, changing the bitrates of audio information for higher efficiency in your mobile phone, MP3 player, or other media devices is a piece of cake.
Helium Audio Joiner is one of the greatest MP3 Joiners that merges MP3, OGG Vorbis, WMA, FLAC, AAC, WAVE and other audio information. The program lets you insert silence between MP3 files, which enables you enter time in seconds. The MP3 Combiner enables you outline the audio title, style, yr, remark, artist and album identify.
excellent post, very іnformative. I ԝօpnder why the opposite experts of thiѕ sector don’t notice
this. You should procеeⅾ your writing. I’m confident, you have a grеat readers’ base already!
Ꮮink exchange is nothing else however it is only placing the other person’s webpage link on your paցe at prоper place and other
person will also dο similar іn favor of you.
My blog post – local seo around Munster in 46321
free download video porn movie psk gratis download bokep jepang
2016 video sex 3gp free download aplikasi bokep jepang bokepindo twitter artis porno video man terbaik
di indonesia dowload video xxx … pornoanimasi downloadbokepcepat filmh…
Компания «АВИАПРОДУКТ» производит такое оборудование, как: аэродромные тормозные тележки нового поколения АТТ-ВПП, оптические линейки типа ОЛ-1, аэродромные электрораспределительные колонки СК-100, аэродромные выпрямители АВ-2М, багажные и контейнерные тележки, аэродромные удлинители и т. д.
https://aviaproduct.ru/remontnye-materialy-dlya-aerodroma/ Холодный ремонтный материал «ХРМ-2» — это уникальная российская разработка, которая уже успела зарекомендовать себя на российском рынке. «ХРМ-2» предназначен для выполнения ремонта сколов, выбоин, раковин, поверхностных разрушений цементобетонных монолитных и сборных покрытий аэродромов, автомобильных дорог, мостов и др. спецсооружений.
Ищете, где купить тросы, трос грозозащитный?
Компания Метизы – крупный поставщик длина троса от лучших производителей на территории Оренбургская область.
Вся продукция сертифицирована и имеет необходимые маркировки.
+7(4862)25-54-37
Сервис помощи выпускникам №1 в стране. Работаем с 2012 года. купить курсовую, дипломную или любую другую студенческую работу можно у нас автор 24 ру
Дизайн человека
I like what you guys tend to be up too. This type of clever work and coverage!
Keep up the superb works guys I’ve incorporated you
guys to my blogroll.
Злое
Кэндимен
Definitely believe that which you said. Your favorite reason appeared to
be on the web the simplest thing to be aware of. I say to you,
I certainly get irked while people think about
worries that they plainly don’t know about. You
managed to hit the nail upon the top as well as defined
out the whole thing without having side effect , people can take a
signal. Will probably be back to get more. Thanks
Соври мне правду
Yes! Finally something about vivoslot online.
My developer is trying to convince me to move to .net from PHP.
I have always disliked the idea because of the costs.
But he’s tryiong none the less. I’ve been using Movable-type on numerous websites for about a year and am concerned about
switching to another platform. I have heard fantastic things about blogengine.net.
Is there a way I can import all my wordpress content into
it? Any kind of help would be greatly appreciated!
my web page – whatsapp mod terbaru
օbviously like your web-site but you need to
test the spelling on several оf your posts. Many of them aare
rife with sρellling issues aand I in finding it very bothersome to terll the truth
һowever I’ll сertainly come again аgain.
Hereе is my webpage – lusofonia
Специалисты АВТОГУД имеют большой опыт кузовного ремонта и способны восстановить первоначальную геометрию кузова даже после серьезных повреждений кузова. В кузовном цеху используется самое современное оборудование.
https://avtogud.pro/mercedes/ Окраска кузова в сервисном центре АВТОГУД опирается на заводские стандарты. Имеется собственный окрасочный цех, где кузова проходят несколько уровней покрытия. Так же в окрасочном цехе делается аэрография.
2135
Great post. I was checking constantly this blog and I’m impressed!
Extremely useful information particularly the last part :
) I care for such information much. I was looking for this
certain info for a long time. Thank you and best
of luck.
Ηmm it looks ⅼikе your blog ate my first ϲоmment
(it was super long) soo I guess I’ll just sᥙm it up what
I submitted and say, I’m thoroughly enjoying your blog.
I too am аn aspiring blog writer bᥙt I’m still new to everything.
Do you have any tips and hints for newbie blog writers? I’d
rеally appreciate it.
Here is my ԝeeb page … 10Mm lashes
WOW just what I was searching for. Came here by searching for mposlot.com
http://agrotrans.5nx.org/viewtopic.php?f=2&t=53763
First off I want to say excellent blog! I had a quick question in which I’d like to ask if you don’t
mind. I was curious to find out how you center yourself and clear your
head before writing. I’ve had a tough time clearing my mind in getting my thoughts out there.
I truly do take pleasure in writing however it just seems like the first 10 to
15 minutes are lost simply just trying to figure out how
to begin. Any ideas or hints? Appreciate it!
https://beldcom.com/
I visit each day a few websites and sites to read articles or reviews, but this weblog presents feature based articles.
http://shumka.at.ua/forum/39-2459-1
ivermectin for sale on ebay
Online shop for womens clothing and accessories based in the UK strives to provide high quality products from the most reliable companies in the world.
We are opening a marketplace for shoppers to find the latest and greatest in-demand products at incredibly low prices.
https://fas.st/d3rNK
Easy MP3 Cutter Joiner Editor is a free device to simply split, merge or edit MP3 information, and in addition supports many other formats. Click on “Add File” button to import the MP3 information which you prefer [url]https://www.mp3joiner.org[/url] to merge into one. Or choose all of the MP3 information or the folder the place the MP3 audio are situated after which immediately drag and drop them to the principle window of the MP3 combiner.
Lacking in perform, ugly, and arduous to make use of, Free MP3 Cutter Joiner has a very specific use. But on condition that Audacity is also free and presents a full suite of extra user-friendly audio tools, I don’t know why you wouldn’t select that as an alternative.
Direct MP3 Joiner is a simple and quick audio instrument to combine MP3s , in addition to merge or be part of MP3 recordsdata. With Direct MP3 Joiner, you can be part of multiple music MP3 files into a bigger MP3 file in a cut up second. You can merge, mix and be a part of MP3 audio recordsdata with blazing speed, without recompressing and with out high quality loss. Our MP3 Joiner works with audio recordsdata instantly and the joined MP3 tune can be prepared virtually immediately. With our MP3 Merger, you can be part of your separate audiobook chapters into one big audiobook or combine a number of music tracks into one non-stop audio CD.
This free MP3 joiner helps a large amount of enter audio formats including MP3, WMA, WAV, AAC, FLAC, OGG, APE, AC3, AIFF, MP2, M4A, CDA, VOX, RA, RAM, TTA and far more as supply codecs [url]https://www.mp3joiner.org[/url]. Any audio recordsdata and audiobooks could be joined to the most well-liked audio formats as MP3, OGG, WMA, WAV, and many others.
Audio Merger : MP3 Joiner App Are Also Cuting Audio in Audio Helps All the Audio Files Including Mp3,Wav and Other Audio Recordsdata. You may also edit the metadata and the album art of the audio information which are edited with Easy MP3 Cutter Joiner Editor.
I exploit the program to merge audio book recordsdata. Completely satisfied with it. MP3 Joiner allows you reviewing the MP3 ID3 tag info. – Create Music Slicing and Merging Different MP3 Information. Whether you should get MP3 from DVD, on-line streaming websites or add information from your pc, you should utilize this system to extract the MP3 recordsdata for you with ease. The section will extract MP3 from MP4 information for example.
MP3 Joiner Express is the best software for join MPEG-1 Audio Layer three (MP3) audio files. It is vitally simple to use with none special setting. You may quickly add the mp3 files. Join your MP3 recordsdata and keep all MP3 frames. Be a part of your MP3 file with out re-encoding it, so quick past your imagination.
MediaJoin is another MP3 Joiner with friendly interface. The program is not solely merging audio recordsdata in different codecs, but additionally joining media information. You possibly can add MP3, OGG, WMA, WAV audio codecs as well as MPEG, AVI and WMV recordsdata. It needs to be the free audio and video joiner software program.
Добрый день.
Посоветуйте отличную онлайн-типографию для заказа брошюр
Могу посоветовать одну типографию , качество, цены и скорость у них хорошее,
но они размещаются в Красноярске, а мне хотелось бы в Новосибирске.
Здесь печать и изготовление книг https://kraft-pt.ru/products/knigi
Понимая значимость образования позитивного развития нашего близкого будущего, мы решили создать на сайте раздел для публикаций нашими участниками их видения путей достижения позитивных, положительных результатов развития общества . Создай свои Проекты будущего
tadalafil 40 mg
Ищете, где купить тросы, трос для лебедки?
Компания Метизы – крупный поставщик изготовление тросов от лучших производителей на территории Воронежская область.
Вся продукция сертифицирована и имеет необходимые маркировки.
+7(4862)25-54-37
med pharmacy
1 Мая челябинские единороссы устроят междусобойчик с \молодогвардейцами\”. а ЛДПР выведет на улицу БТР”Традиционно 1 мая в Челябинске пройдут митинги и шествия. Ради этого на полчаса будет перекрыт проспект Ленина. Как передает корреспондент \Нового Региона\” начнут праздник профсою”
Семейное обучение г. Мытищи.Наша школа для тех, кому необходимо обучение для жизни, а не для тестов. Кто ищет команду единомышленников, с которыми можно согласованно растить авторскую позицию ребенка.
Индивидуальная учебная линия для каждого ученика. Мы работаем по советским общеобразовательным школьным программам, но темп и принципы работы подбираем сами, индивидуально под каждого ребенка. http://asmechta.ru Балет – это нелегкое искусство и труд, которые требуют самоорганизации, дисциплины, целеустремленности. Регулярные занятия развивают:
моральную устойчивость;.
навык понимания собственного тела, пластичность, гибкость;
умение придерживаться дисциплины;
ответственность, трудолюбие;
чувствовать музыка и понимать ритм.
Не утверждаем, что идеальны, но день за днем совершенствуем методы и систему работы — следим за качеством занятий, проводим анализ. http://asmechta.ru/semeynoe-obuchenie/ Наша семейная школа с отличными учителями, профессионалами, которые ведут дополнительные кружки в нашей студии.
Если ищите ремонт или замену автомобильного стекла, то вы попали в нужное место. Автостекло77 занимается продажей, установкой и ремонтом стекол от малолитражек до автофур. Наша основная цель помочь клиентам заменить или отремонтировать стекла: лобовое, боковое и заднее.
https://autosteklo77.com/magazin/folder/bokovoye-194 Компания «Автостекло77» предлагает своим клиентам широкий спектр услуг по продаже, ремонту, замене и обслуживанию автомобильных стекол. Все сопутствующие работы проводятся исключительно высококвалифицированными сотрудниками, имеющими значительный профессиональный опыт, на современном технологичном оборудовании.
Покупаете первый автомобиль или хотите обменять свою старенькую машину на что-то поновее – в AVALON рады всем!
https://avaloncars.ru/trade-in Мы выстроили процесс для комфортного обслуживания клиентов.
Удобный график работы, профессиональная работа менеджеров, выгодные условия продажи автомобилей с пробегом – все сделано для того, чтобы вы остались довольны посещением AVALON и рекомендовали нас друзьям и родственникам.
Thesis statement examples https://myspace.com/essaypro57
UYhjhgTDkJHVy
Специалисты АВТОГУД имеют большой опыт кузовного ремонта и способны восстановить первоначальную геометрию кузова даже после серьезных повреждений кузова. В кузовном цеху используется самое современное оборудование.
https://avtogud.pro/contact Окраска кузова в сервисном центре АВТОГУД опирается на заводские стандарты. Имеется собственный окрасочный цех, где кузова проходят несколько уровней покрытия. Так же в окрасочном цехе делается аэрография.
Trsuted Online Casino Malaysia http://gm231.com/comments/feed/#Comments for Game Mania – More info!
Xm193 ammo 1000 rounds
no prescription cheap cialis
부산탈모병원
Buy 300acc blackout online
농구중계
Montenegro real estate 646ce32
Победитель лотереи Saturday Lotto о себе и планах на жизнь:
Мы всегда понимали, что наши игроки — личности интересные и выдающиеся!
Вот, к примеру, рассказ одного из наших победителей. Максим Г. угадал все номера второй категории “5+S” и выиграл 8 736,07 USD (или 11 893,89 AUD австралийских долларов) в в Австралийской игре Saturday Lotto.
Максим рассказал о себе и поделился будущими планами:
— Расскажите о себе: Какая у Вас профессия? Чем вы увлекаетесь, на что тратите свободное время?
На Ваши вопросы с удовольствием отвечу. Мне 53 года, по профессии я механик судовых холодильных установок. Много лет увлекаюсь игрой на гитаре. Люблю слушать и играть блюз, люблю природу и стараюсь по возможности непременно выехать на несколько дней из города.
— Что мотивировало Вас начать участвовать в зарубежных лотереях онлайн? Как Вы отыскали наш сайт Agentlotto.Org?
Участвовать в лотереях я всегда любил и покупал систематически билеты на другом лотто сайте ***. Не знаю, почему там, как-то про него чаще видел информацию в сети.
Серьезных выигрышей не было. На то, что выигрывал, сразу брал билеты. Ситуация эта продолжалась до тех пор, пока я не решил потестировать Ваш сайт. Скажу честно, смотрел его раньше, но не особо пристально! Совсем недавно решился изучить повнимательнее.
Причина, по которой я перешёл к вам, — возможность приобрести 1 билет любой лотереи (чего нет у ***), удобный интерфейс, все просто и понятно, также приемлемая ценовая политика на покупаемые билеты и быстрая обратная связь.
— Расскажите о самом серьезном выигрыше, который вам довелось сорвать: в какую лотерею, сколько Вы выиграли, как Вы отреагировали на победу?
Самый крупный выигрыш за все время выпал только с Вами, на Вашем сайте! И я думаю, что это не просто так…!!!
— Представьте, что Вы сорвали грандиозный Джекпот. Как Вы потратите главный приз? Поведайте немного о своих планах.
Если посчастливится сорвать Джекпот, бОльшую часть потрачу на помощь тем, кто точно в этом нуждается. Для себя же открою сеть пабов, где будут играть только живой блюз!
***
Мы поздравляем нашего замечательного участника с выигрышем! Желаем ему дальнейших побед и осуществления мечты — ведь кто не любит хорошую музыку?
А сегодня мы предлагаем вам поучаствовать в лучшие иностранные лотереи вместе с нами!
Готовы поспорить, Вам бы точно не натерли карман $ 241 000 000 USD! лотереи Powerball
Montenegro real estate a199cbe
Montenegro real estate 5593fe3
miami limo
Назначен директор челябинского зоопарка. Директором челябинского зоопарка назначен 35-летний Алексей Солдаткин. Об этом сообщили в управлении культуры города.Как сообщили в челябинском зоопарке, Алексей Солдаткин пока не дает комме
Thesis statement ghostwriter websites usa https://ugienergylink.com/how-can-a-polar-vortex-raise-costs-for-your-home-energy-bills/
UYhjhgTDkJHVy
Гадаю дистанционно 30 лет. Оставьте ТОЛЬКО !!! сообщение в Вотцап на телефон +1 (248) 730-4177. Я С Вами свяжусь сама. На неизвестные звонки не отвечаю
Bc athlete resume http://edubirdie-com.ezblogz.com/23986203/edubirdie-edubirdie-com
UYhjhgTDkJHVy
Help me write medicine book review http://solutionmotivator.my/forum/index.php?action=profile;u=52361
UYhjhgTDkJHVy
A 200 to 300 word essay in apa format arguing https://logobran.com/?p=75036
UYhjhgTDkJHVy
Essays on the consequences of drinking and driving studybay reviews
UYhjhgTDkJHVy
High school resume template pdf essaytyper
UYhjhgTDkJHVy
How cover letter робот займер личный кабинет войти
UYhjhgTDkJHVy
Digital libraries+xml research papers EduBirdie
UYhjhgTDkJHVy
Ap world history continuity change over time essay авиасалес официальный сайт дешевые авиабилеты
UYhjhgTDkJHVy
Research for business plan Диссертация на заказ
UYhjhgTDkJHVy
Write my art & architecture movie review обследование зданий
UYhjhgTDkJHVy
Thematic resume loansolo
UYhjhgTDkJHVy
Custom personal essay writing for hire au speedypaper
UYhjhgTDkJHVy
Sri lankan civil war essay микрозайм на карту
UYhjhgTDkJHVy
Cover letter with subject line examples Оценка недвижимости
UYhjhgTDkJHVy
What type of spacing should a cover letter use микрозайм онлайн без истории
UYhjhgTDkJHVy
Literature review cruise industry loansolo
UYhjhgTDkJHVy
Sample essay questions for college admission банк личный кабинет
UYhjhgTDkJHVy
Diet program business plan paperhelp
UYhjhgTDkJHVy
Cover letter film production company studybay US
UYhjhgTDkJHVy
Objective for teachers assistant resume essay shark login
UYhjhgTDkJHVy
How to write function in mysql example essaypro
UYhjhgTDkJHVy
How a good resume should look cashnetusa,com
UYhjhgTDkJHVy
Custom university article ideas обследование конструкций здания
UYhjhgTDkJHVy
Template for internship resume payday loans online
UYhjhgTDkJHVy
Popular annotated bibliography proofreading sites au займ онлайн
UYhjhgTDkJHVy
Dracula book report EduBirdie
UYhjhgTDkJHVy
Essay on man analysis epistle 2 speedypaper
UYhjhgTDkJHVy
Compare and contrast essay mexican revolution edubirdie.com
UYhjhgTDkJHVy
Strategies for taking essay tests займы онлайн срочно без отказа круглосуточно
UYhjhgTDkJHVy
Custom thesis editing site uk обследование зданий и сооружений
UYhjhgTDkJHVy
Desperado essay interviews авиасалес официальный сайт дешевые авиабилеты
UYhjhgTDkJHVy
Objectives examples for resume studybay
UYhjhgTDkJHVy
Analytical research writing essayshark.com
UYhjhgTDkJHVy
Progress and resume and ohio essaypro login
UYhjhgTDkJHVy
Professional thesis statement ghostwriting website for masters cashnetusa.com/approved
UYhjhgTDkJHVy
Best school essay ghostwriter services usa studybay
UYhjhgTDkJHVy
Resume for free download сити займ
UYhjhgTDkJHVy
Popular persuasive essay ghostwriter services for school speedypaper
UYhjhgTDkJHVy
Ielts recent essay questions 2019 essay shark login
UYhjhgTDkJHVy
Success essays free Рђuthor24
UYhjhgTDkJHVy
College proofreading for hire gb EssayTyper
UYhjhgTDkJHVy
Suggested topics for problem solution essays essaypro
UYhjhgTDkJHVy
Cheap cheap essay proofreading sites au studybay login
UYhjhgTDkJHVy
Lse research papers in environmental and spatial analysis author24.ru вход
UYhjhgTDkJHVy
The drum john scott essay essaypro login
UYhjhgTDkJHVy
Help with government paper EssayPro
UYhjhgTDkJHVy
Purchase and download research papers CashNetUsa
UYhjhgTDkJHVy
Resume ghostwriters websites uk Оценка недвижимости
UYhjhgTDkJHVy
Popular phd essay editor for hire for masters EssayTyper
UYhjhgTDkJHVy
Top proofreading website for phd заказать смету
UYhjhgTDkJHVy
Write education thesis statement edubirdie.com
UYhjhgTDkJHVy
Essays on gay couples adopting children деловые займы официальный сайт
UYhjhgTDkJHVy
Personal statement assistance speedypaper
UYhjhgTDkJHVy
How to write a short company description essaypro
UYhjhgTDkJHVy
Intermediate previous question papers 2nd year essaytyper
UYhjhgTDkJHVy
Thesis help writing сити кредит
UYhjhgTDkJHVy
Adam smith assembly essay full 2 filmbay academics iv 41 h html essaypeo
UYhjhgTDkJHVy
Trusted Online Casino Malaysia http://gm231.com/gm231-online-sportsbook-malaysia-sports-betting-odds/#{GM231|Free Online Sportsbook Malaysia | – {Online Casino Malaysia|Click here|More info|Show more}{!|…|>>>|!..}
Texas history essay contest online dissertation writing
UYhjhgTDkJHVy
Cheap dissertation conclusion editing site for mba aviasales.ru
UYhjhgTDkJHVy
Esl expository essay ghostwriter website for masters essaypro
UYhjhgTDkJHVy
Top blog writing sites for masters отличные наличные сыктывкар
UYhjhgTDkJHVy
Colorado home essay contest speedypaper
UYhjhgTDkJHVy
A level essays free fdnjh24
UYhjhgTDkJHVy
How to write to organiz acm citation generator
UYhjhgTDkJHVy
Help with pre calc homework essaypro
UYhjhgTDkJHVy
Free help with essays Аuthor24 ru
UYhjhgTDkJHVy
Dr phil doctoral dissertation EssayPro
UYhjhgTDkJHVy
Esl dissertation conclusion editing websites uk онлайн займы без в казахстане
UYhjhgTDkJHVy
Registrar resume cover letter studybay
UYhjhgTDkJHVy
Top book review ghostwriter for hire авиасейлс купить билеты
UYhjhgTDkJHVy
Top bibliography ghostwriter sites buy essay
UYhjhgTDkJHVy
Junior cert science coursework a answers EssayTyper
UYhjhgTDkJHVy
How to write an essay from an outline essaypro
UYhjhgTDkJHVy
Best biography writers websites for phd CashNetUsa Login
UYhjhgTDkJHVy
Professional case study editor websites for college studybay sign up
UYhjhgTDkJHVy
Top assignment editor service for phd Author24 ru
UYhjhgTDkJHVy
Insights essay buy research paper
UYhjhgTDkJHVy
One page research paper proposal pro essay
UYhjhgTDkJHVy
Primary school homework statistics reviews for cashnetusa
UYhjhgTDkJHVy
Resume for network technician for entry level топ банков по кредитам
UYhjhgTDkJHVy
Write a short memo to the fan company a partners оне займ
UYhjhgTDkJHVy
С 2012 г. с помощью Pinterest помогаю продавать товар в Etsy, что дает Заказчикам до 100 000 usd в месяц. Работаю также в amazon, ebay, shopify и c русскими сайтами. Пример: https://youtu.be/v-b2HL-ZF4c
Biography ghostwriter website gb автор24 официальный сайт
UYhjhgTDkJHVy
Graphic designer resume templet автор24.ру личный кабинет войти в личный кабинет
UYhjhgTDkJHVy
Apa format citing websites no author EssayPro
UYhjhgTDkJHVy
Esl literature review editing services for college обследование зданий
UYhjhgTDkJHVy
How to spend your summer vacation essay in english займ ру
UYhjhgTDkJHVy
Custom university dissertation introduction topics заем онлайн
UYhjhgTDkJHVy
Bronwyn lea essay займы онлайн
UYhjhgTDkJHVy
Critical essay on candide loansolo
UYhjhgTDkJHVy
Essays ghostwriting services online автор24 ру официальный сайт
UYhjhgTDkJHVy
Top dissertation hypothesis editor site gb Payday Loans
UYhjhgTDkJHVy
Hook thesis blueprint loansolo Login
UYhjhgTDkJHVy
Algebra homework plot a line studybay login
UYhjhgTDkJHVy
Effective homework practices studybay Australia
UYhjhgTDkJHVy
Ownership of a business plan cashnetusa.
UYhjhgTDkJHVy
Research proposal ghostwriting sites EssayPro
UYhjhgTDkJHVy
Professional business plan proofreading sites for mba Диссертация на заказ
UYhjhgTDkJHVy
Do my physics article review cashnetusa
UYhjhgTDkJHVy
Free essay about periowave Строительная экспертиза
UYhjhgTDkJHVy
Proficient computer skills resume sample топ кредит
UYhjhgTDkJHVy
Popular dissertation hypothesis ghostwriter for hire проект сзз
UYhjhgTDkJHVy
Вчера звонили по этому номеру 9193383665, это точно мошенники!
Представляются продавцом с авито.
Подозрительный телефон посмотрела тут https://call-hunter.com/phone/9193383665
И была права! Отвлекают людей.
Не ведитесь на их уловки.
Singer prebisch thesis terms of trade essaytyper review
UYhjhgTDkJHVy
Custom paper writing sites for phd studybay
UYhjhgTDkJHVy
An alternative to the chronological format resume is esssay pro
UYhjhgTDkJHVy
Pay for my cheap creative essay on brexit банк личный кабинет
UYhjhgTDkJHVy
За выходные на дорогах Челябинска сбили двух пьяных пешеходов. В минувшую пятницу ранним утром на Троицком тракте 49-летний водитель автомобиля «Камаз» сбил пешехода. 20-летний молодой человек переходил проезжую часть дороги
Элементы лестниц оптом, кухни на заказ, двери из массива дуба https://www.ekolestnica.ru Большой выбор изделий из дерева (дуб, бук, ясень, береза, сосна) оптом балясины, перила, ступени для лестниц, двери из массива дуба, мебельный щит! На рынке 15 лет, доставка в любые регионы!
С 2012 г. с помощью Pinterest помогаю продавать товар в Etsy, что дает Заказчикам до 100 000 usd в месяц. Работаю также в amazon, ebay, shopify и c русскими сайтами. Короткий Пример: https://youtu.be/v-b2HL-ZF4c
С 2012 г. с помощью Pinterest помогаю продавать товар в Etsy http://1541.ru что дает Заказчикам до 100 000 usd в месяц. Работаю также в amazon, ebay, shopify и c личными сайтами. Цена за месяц рекламы от 300 usd
Architecture thesis topics list pdf http://maps.google.co.ke/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Professional papers writers site online http://google.si/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
How to write a ucas personal statement for teaching https://google.ee/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Signet classics scholarship essay contest 2010 http://maps.google.fr/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Popular admission essay proofreading service for phd http://google.gm/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Resume tech style http://www.google.be/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Top report writers sites gb http://www.bon-vivant.net/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Free essays on trinity by leon uris http://images.google.com.ua/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Professional critical essay writers services us http://google.ps/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Custom argumentative essay writer for hire for school http://images.google.cn/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Sample graphic design resume objective http://maps.google.com.gh/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Buy cheap descriptive essay online https://www.google.co.vi/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Thesis front page lyx https://google.me/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Cheap speech ghostwriting websites au EssayPro
UYhjhgTDkJHVy
Trusted Online Casino Malaysia http://gm231.com/gm231-best-online-slot-games-malaysia-slots-918kiss-xe88/#{Best Online Slot Games Malaysia | Slots | – {Online Casino Malaysia|Click here|More info|Show more}{!|…|>>>|!..}
Mysore (or Mysuru), a city in India’s southwestern Karnataka state, was the capital of the Kingdom of Mysore from 1399 to 1947. In its center is opulent Mysore Palace, seat of the former ruling Wodeyar dynasty. The palace blends Hindu, Islamic, Gothic and Rajput styles. Mysore is also home to the centuries-old Devaraja Market, filled with spices, silk and sandalwood.
Mysuru
Mysore (or Mysuru), a city in India’s southwestern Karnataka state, was the capital of the Kingdom of Mysore from 1399 to 1947. In its center is opulent Mysore Palace, seat of the former ruling Wodeyar dynasty. The palace blends Hindu, Islamic, Gothic and Rajput styles. Mysore is also home to the centuries-old Devaraja Market, filled with spices, silk and sandalwood.
Pay to write analysis essay on pokemon go https://google.com.br/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Pay to do best cheap essay on civil war http://centralcupon.cuponius.com.ar/redirect/redirv6.php?idR=1274866&url=http://bestessayservicereview.com/
UYhjhgTDkJHVy
Resume wordpress http://maps.google.lu/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Supply chain performance measurement a literature review http://google.im/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Duck tour business plan http://rusremesla.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://bestessayservicereview.com/
UYhjhgTDkJHVy
Master thesis internal communication EssayPro
UYhjhgTDkJHVy
Sap abap certified resume sample esssay pro
UYhjhgTDkJHVy
Apply job letter https://www.google.nu/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Analyzing a film essay EssayPro
UYhjhgTDkJHVy
Индивидуальное проектирование и строительство дома под ключ – видео советы бесплатно
Cover letter sample graduate accountant http://www.608788.com/gourl.asp?url=https://papershelps.org
UYhjhgTDkJHVy
Popular research paper ghostwriters services for mba https://nvl.vbent.org/kvso/redir.php?goto=https://papershelps.org
UYhjhgTDkJHVy
Custom college essay ghostwriter websites us http://asianallies.org/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Sample teaching cover letter for new teachers http://tdfocus.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://bestessayservicereview.com/
UYhjhgTDkJHVy
Narrative of a graduation party essay studybay
UYhjhgTDkJHVy
An essay on brains and beauty https://www.fashionbiz.co.kr/redirect.asp?url=https://papershelps.org
UYhjhgTDkJHVy
Dissertation evaluation training http://alumnae-westoverschool.org/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Top blog proofreading site au http://maps.google.ba/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
How to write daily activities report https://www.aroeleven.com.br/click_email?cliente=PROFIBUS&campanha=profinews35&link=https://papershelps.org
UYhjhgTDkJHVy
James monroe middle school homework links in albuquerque http://artsoffrance.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Quality assurance business analyst resume https://katstat.ru/go.php?url=https://papershelps.org
UYhjhgTDkJHVy
Cause and effect essay on obesity https://maps.google.com.qa/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Pay for speech dissertation introduction https://brettterpstra.com/share/fymdproxy.php?url=https://papershelps.org
UYhjhgTDkJHVy
Write a program that will calculate the factorial of number http://de.itsbetter.com/gourl/?url=https://essaytyper.cm/
UYhjhgTDkJHVy
Researdh methodology for research papers http://americanwesthomesblog.biz/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Cheap college dissertation conclusion advice http://apps.vienna.at/feat/microsite/webcams/welcome.asp?url=bestessayservicereview.com
UYhjhgTDkJHVy
Customerwrtting http://easyfun.biz/email_location_track.php?eid=6577&role=ich&type=edm&to=https://papershelps.org
UYhjhgTDkJHVy
Popular phd essay writer websites for university http://brand-2011.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Accounting homework help studybay
UYhjhgTDkJHVy
Making a resume with only one job http://berrybed.com:443/bitrix/redirect.php?event1=&event2=&event3=&goto=https://essaytyper.cm/
UYhjhgTDkJHVy
Custom resume ghostwriter site for college https://acgso1.com/wp-admin/admin-ajax.php?action=991c8a14a3cbf2367a362127495b7fd3&url=https%3A%2F%2Fpapershelps.org
UYhjhgTDkJHVy
Cheap essay writer sites for college http://dearjennifer.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Contoh essay bi pmr http://www.google.cg/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Essay on censorship in music https://images.google.co.ve/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Professional admission essay ghostwriting website usa https://google.co.ke/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Broadway resume special skills http://peleshair.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Smoking habits essay http://www.lumc-online.org/System/Login.asp?id=44561&Referer=https://essaytyper.cm/
UYhjhgTDkJHVy
Cover letter for technical manager position http://video.fc2.com/exlink.php?uri=https%3A%2F%2Fbestessayservicereview.com%2F
UYhjhgTDkJHVy
Small topics to write about https://www.google.net/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Robert atwan essays https://google.ht/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Gun control argumentative essay https://www.worldcruising.com/extern.aspx?ctype=1&adid=89&pagid=0&src=https://papershelps.org
UYhjhgTDkJHVy
Esl custom essay writing service for university http://www.komus-opt.ru/bitrix/rk.php?goto=https://essaytyper.cm/
UYhjhgTDkJHVy
Buy research paper college https://www.depmode.com/go.php?https://papershelps.org
UYhjhgTDkJHVy
Free small business business plan http://dobrye-ruki.ru/go?https://papershelps.org
UYhjhgTDkJHVy
Howto write a matrimonial bio data https://www.google.cl/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Essays about grandmothers http://web4everyone.net/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Юридическая помощь по любым правовым вопросам в Москве и Московской области. Защита и представительство, составление документов. Консультация по телефону и на сайте бесплатно.
Задать вопросы и получить помощь юриста вы можете на сайте, 7 дней в неделю, без выходных:
Получить консультацию юриста в Москве
Qa web services sample resume http://factsmanagement.info/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Best dissertation methodology writer website gb http://theredish.com/showimg?v=N&img=https://bestessayservicereview.com/
UYhjhgTDkJHVy
Cover letter for commercial lease application http://www.lexingtonsc.org/Redirect.aspx?destination=https://essaypro.me/
UYhjhgTDkJHVy
Trusted Online Casino Malaysia http://gm231.com/gm231-live-casino-malaysia-baccarat-blackjack-roulette/#{Play at GM231- Best Live Casino Malaysia| – {Online Casino Malaysia|Click here|More info|Show more}{!|…|>>>|!..}
https://geni.us/Z36xqK3 leather backpack for ladies
https://geni.us/Z36xqK3 leather backpack for females
Celebration christmas essay http://www.thelateshow.biz/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Professional resume format for administration executive https://www.google.com.py/url?q=https://buyessayreviews.com
UYhjhgTDkJHVy
Indoor go kart track business plan http://ctbuilderdirect.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
How to write pound symbol from keyboard http://denizbankonline.net/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
On aura tout essaye lyrics http://tools-world.ru/bitrix/rk.php?goto=https://buyessayreviews.com/studybay-com/
UYhjhgTDkJHVy
Research paper template word http://www.google.cl/url?q=https://buyessayreviews.com/essaypro-com/
UYhjhgTDkJHVy
Samples of experimental research papers http://images.google.mg/url?q=https://buyessayreviews.com/essaytyper-com-review/
UYhjhgTDkJHVy
Best masters essay writing website online https://google.com.tn/url?q=https://bestessayservicereview.com
UYhjhgTDkJHVy
Research reports format https://xn--80abjdxyg2b.xn--p1ai/chat/process-essay-samples-2022-2/
UYhjhgTDkJHVy
Pay to do sociology dissertation conclusion http://wavetrick.com/__media__/js/netsoltrademark.php?d=papershelps.org
UYhjhgTDkJHVy
Thesis on the declaration of independence https://www.google.rs/url?q=https://papershelps.org
Custom speech ghostwriter sites online http://bonusdunyasi.com/__media__/js/netsoltrademark.php?d=papershelps.org
Custom personal essay writing site for college https://maps.google.sh/url?q=https://buyessayreviews.com
Scientific laboratory http://apps.vienna.at/feat/microsite/webcams/welcome.asp?url=essaytyper.cm
Best phd essay proofreading for hire for mba http://sloopart.info/__media__/js/netsoltrademark.php?d=papershelps.org
Custom best essay ghostwriter websites for mba http://www.google.com/url?sa=t&url=https%3A%2F%2Fwww.essaypro.me
Trusted Online Casino Malaysia http://gm231.com/download-now/#Game Mania – Click here!
where to buy ivermectin pills
tadalafil 100mg india
buy oral ivermectin
buy brand viagra online
cialis 10mg sale
lexapro 2.5 mg
azithromycin gel
where can i buy tretinoin cream
where can i get doxycycline uk
diclofenac 1 topical gel
cialis|buy cialis|generic cialis|cialis pills|buy cialis online|cialis for sale
viagra pills
viagra pills
cialis online paypal
best canadian online pharmacy cialis
brand name cialis prices
viagra brand name in india
buy cialis soft tabs online
tadalafil 10 mg online
sildenafil 150mg tablets
generic viagra in canada
order tadalafil
generic viagra cheap
cheap price sildenafil 100 mg
Free fitness instructor job cover letter http://carexpo.ru/bitrix/rk.php?id=80&event1=banner&event2=click&event3=1+/+0%5D+2%5D+?????????+2017+&goto=https://papershelps.org
Photo essays of americans https://maps.google.cz/url?q=https://buyessayreviews.com
Resume shangin http://www.badmoon-racing.jp/frame/?url=https://papershelps.org
lowest prices online pharmacy sildenafil
Help me write a funny speech http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/1671292
Top dissertation methodology ghostwriter websites for mba https://cse.google.to/url?q=https://papershelps.org
How to write good luck in welsh http://images.google.cn/url?q=https://buyessayreviews.com/essaypro-com/
3rd slave hard disk error press f1 resume http://pennyapplegate.com/SearchPoint/redir.asp?reg_id=pTypes&sname=/searchpoint/search.asp&lid=0&sponsor=LAN&url=https://essaypro.me/
Popular writers site http://ip.tool.chinaz.com/?ip=essaypro.me
The merchant of venice gcse language and literature coursework http://images.google.com.gi/url?q=https://buyessayreviews.com/essaytyper-com-review/
International essay contest 2005 EssayPro
Ideas essay scholarship https://www.google.com.mt/url?q=https://bestessayservicereview.com
Thesis on parking study http://google.mg/url?q=https://buyessayreviews.com/essaytyper-com-review/
Esl dissertation conclusion ghostwriters services essaytyper
Cover letter templates and samples nursing https://maps.google.ru/url?q=https://buyessayreviews.com/studybay-com/
Sample of a resume cover sheet http://mybio-market.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://essaypro.me/
Esl dissertation hypothesis writer website ca http://uhlalainsumos.cl/2016/11/14/noticia-test-1/
propranolol buy online india
Miranda rights essay papers http://www.google.hr/url?q=https://buyessayreviews.com/essaytyper-com-review/
Masters essay editing websites us http://google.lt/url?q=https://buyessayreviews.com/studybay-com/
Professional definition essay writers for hire for college http://www.google.td/url?q=https://buyessayreviews.com/studybay-com/
Examples for research paper http://www.sunway.ru/bitrix/rk.php?id=2&event1=banner&event2=click&event3=1+%2F+%5B2%5D+%5BTOP%5D+%C7%E0%E3%EB%F3%F8%EA%E0+2&goto=https://papershelps.org
Popular personal essay ghostwriter websites au http://www.massimobosco.net/eng/sez/go.asp?url=https://buyessayreviews.com/essaypro-com/
baclofen 10 mg tablet price
50mg bupropion
where to buy biaxin
lipitor canada pharmacy
estrace pills for ivf
trazodone buy
Array homework pass template http://bowlingcoach.co.uk/__media__/js/netsoltrademark.php?d=papershelps.org
Research paper on a b c analysis pdf http://www.mazda-avtomir.kz/bitrix/rk.php?goto=https://essaytyper.cm/
Top phd paper ideas http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/939894
Pay to get criminal law annotated bibliography EssayPro
How to write a documentary analysis http://www.naylorwealthmanagement.com/redirect.cfm?target=https://buyessayreviews.com/essaypro-com/
Cheap school article review help http://google.com.pa/url?q=https://buyessayreviews.com/essaytyper-com-review/
Good essay titles for kids https://www.dorsten.de/Externer_Link.asp?ziel=papershelps.org
levaquin antibiotics
Custom paper ghostwriters services for college http://clublove.us/__media__/js/netsoltrademark.php?d=papershelps.org
Help me write chemistry dissertation methodology http://maps.google.ki/url?q=https://buyessayreviews.com/essaypro-com/
Complete free online papers research http://zfanta.weehan.com/board/4142055
stromectol cream
Example free objective resume https://sunnylivingflorida.com/writing-a-process-essay-examples-2022/
College essay proofreading website ca https://maps.google.com.ni/url?q=https://buyessayreviews.com/essaypro-com/
best tadalafil prices
6th grade essay suggestions EssayPro
Custom creative writing writing service for college https://www.google.co.in/url?q=https://buyessayreviews.com/essaytyper-com-review/
Professional persuasive essay ghostwriters site uk https://images.google.co.in/url?q=https://buyessayreviews.com/essaytyper-com-review/
tadalafil best online pharmacy
Write my custom analysis essay on pokemon go http://poselenia.ru/ext_link?url=https://buyessayreviews.com/
Ps3 dvd resume https://griffin-realstate.com/essaypro-ae-essaypro-reviews-reddit-essaypro-coupon-login-to-essaypro-essaypro-faq/
Labor related resume http://zfanta.weehan.com/board/3818752
Professional university papers help http://www.google.mu/url?q=https://bestessayservicereview.com
Selling writing services http://dir.curezone.com/c.asp?https://bestessayservicereview.com
Thesis about bill clintomn https://images.google.us/url?q=https://buyessayreviews.com/essaypro-com/
Popular presentation editing site for college https://google.com.sl/url?q=https://buyessayreviews.com/essaytyper-com-review/
Sample cover letter for regulatory affairs manager https://maps.google.kg/url?q=https://bestessayservicereview.com
Carl jung the personal and the collective unconscious essay http://gs.orenhofen.de/externerlink.php?goto=https://buyessayreviews.com/
cost for generic cialis
female viagra over the counter
Top dissertation chapter writers websites online http://kentuckychoicerealty.com/SearchPoint/redir.asp?reg_id=pTypes&sname=/searchpoint/search.asp&lid=2&sponsor=COM&url=https://bestessayservicereview.com/
Where do publications go on a resume http://images.google.tg/url?q=https://buyessayreviews.com/essaytyper-com-review/
Do my custom masters essay on hillary clinton http://www.google.co.ck/url?q=https://buyessayreviews.com
Top university descriptive essay ideas http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/1955610
kamagra tablets
Turner thesis main points http://zfanta.weehan.com/board/4431159
Best application letter writers for hire ca https://remingtonpngt34586.jts-blog.com/11177989/does-essaypro-work-essaypro-facebook-essaypro-black-friday-login-to-essaypro-essaypro-terms-and-conditions
generic cialis tablets
Top blog proofreading sites us https://x007.co/writing-a-process-essay-examples-2022-4/
How to write binding keys http://dissertation-help.com/__media__/js/netsoltrademark.php?d=papershelps.org
Custom admission paper ghostwriter site http://underground.co.za/redirect/?url=https://essaytyper.cm/
How to write an art description http://www.idtlearning.com/redirect.aspx?destination=https://bestessayservicereview.com/
Buy custom essay on shakespeare http://www.mazda-avtomir.kz/bitrix/rk.php?goto=https://buyessayreviews.com/essaypro-com/
levitra cost australia
medicine medrol 16 mg
atarax over the counter
Sample graduate school personal statement for engineering https://www.youtulust.com/profile/delia89x191843/
Academic essay ghostwriting service gb https://socialmarkz.com/story611158/essaytyper-review
Thesis survival kit gift https://images.google.co.hu/url?q=https://bestessayservicereview.com
Sample resume of bankruptcy court clerk http://lsmbwiki.busybear.fi/wiki/tiki-index.php?page=UserPageedubirdiecomuga
finasteride 1mg no prescription
Thesis printing binding http://google.co.mz/url?q=https://bestessayservicereview.com
Confidentiality agreement business plan sample http://www.google.ws/url?q=https://buyessayreviews.com/essaytyper-com-review/
buy cheap cialis from canada
Essay on the value of literature http://www-essaypro-com.aboutyoublog.com/11958984/essaypro-youtube-essaypro-ae-how-essaypro-works-essaypro-blog-how-to-write-a-thesis-statement-essaypro-writers-login
What are typical college essay questions EssayPro
Use of sources in essay https://holdendykp38060.buyoutblog.com/9698563/essaypro-promo-code-essaypro-become-a-writer-essayprowriting-login-essaypro-coupon-code-2021-become-a-writer-on-essaypro
Criminal justice workplace observation essays https://www.google.co.ck/url?q=https://buyessayreviews.com
Ask for interview in cover letter http://davinciproject.org/__media__/js/netsoltrademark.php?d=papershelps.org
Template for modeling resume http://irinasikela.com/searchpoint/redir.asp?reg_id=ptypes&sname=/searchpoint/search.asp&lid=1&sponsor=bus&url=https://buyessayreviews.com/
School violence essays https://images.google.cd/url?q=https://buyessayreviews.com/studybay-com/
Essay on natural disasters in pakistan http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/861167
buy 1000 viagra
Example of internship resume http://www.google.ml/url?q=https://buyessayreviews.com/essaypro-com/
Barber clarinet concerto corigliano essay john orchestra samuel third https://google.im/url?q=https://buyessayreviews.com/essaytyper-com-review/
sildenafil buy usa
sildenafil mexico pharmacy
generic cialis online australia
how much is cephalexin
medicine celebrex 200mg
20 mg toradol
neurontin sale
cialis 20 mg discount coupon
where to buy cialis over the counter
buy cialis gel
buy stromectol canada
viagra over the counter nz
buy viagra europe
ivermectin eye drops
robaxin 500 mg tablet
nexium 40 otc
diclofenac 2.5 cream
generic name for ivermectin
purchase clindamycin
where to get viagra online
cialis paypal australia
us generic cialis
cialis 100
ivermectin 3mg tablet
tamoxifen
zithromax antibiotic without prescription
celebrex 200mg uk
cheap cialis canada online
buy soft cialis
what is the cost of cialis
Esl dissertation methodology ghostwriter service usa http://go.xscript.ir/index.php?url=https://papershelps.org
Best dissertation hypothesis writing website for school https://sitesrow.com/story597178/essaypro-headquarters-essaypro-black-friday-2021-essaypro-hiring-essaypro-reddit-promo-code-for-essaypro
Extended essay topics psychology http://www.printrite.co.za/process-essay-samples-2022/
Custom dissertation editing websites for university http://web4everyone.net/__media__/js/netsoltrademark.php?d=papershelps.org
Top letter proofreading sites uk https://wearethelist.com/story608981/essaytyper-review
Researcher resume description https://xn--80abjdxyg2b.xn--p1ai/chat/review-of-essaypro-com-essaypro-active-essaypro-coupons-essaypro-com-login-sign-up-for-essaypro/
Sample apa format research paper outline https://arqma.smartcoinpool.net/question/671675/how-to-do-cursive-letters/
buspar price canada
Custom custom essay on founding fathers http://carmaxautofinance.biz/__media__/js/netsoltrademark.php?d=papershelps.org
Free resume examples high school http://omnimed.ru/bitrix/rk.php?goto=https://buyessayreviews.com/studybay-com/
It recruiter sample resume india http://maps.google.ws/url?q=https://buyessayreviews.com/essaytyper-com-review/
Essay the brain time travel in the brain https://sunnylivingflorida.com/critical-response-essay-example-pdf/
best sildenafil 20mg coupon
Write a formula for hydrogen bromide http://mbdgroup.info/__media__/js/netsoltrademark.php?d=papershelps.org
modafinil over the counter usa
How to write arabic in yahoo messenger http://rbcbuffalo.org/System/Login.asp?id=54200&Referer=https://buyessayreviews.com/essaytyper-com-review/
Best dissertation results writing service for phd http://shorturl4u.blogspot.com/search/?label=https://bestessayservicereview.com/
Mba essay questions leadership https://augustlzku88776.gynoblog.com/11123347/essay-pro-customer-service-number-essaypro-sign-in-essaypro-bidding-bot-essay-pro-con-websites-like-essaypro
purchase generic cialis online
Post production audio engineer resume https://www.google.com/url?q=https://bestessayservicereview.com
Service personal essay https://maps.google.hu/url?q=https://buyessayreviews.com
Best blog proofreading service ca http://zfanta.weehan.com/board/3892205
Zizek essay courtly love EssayPro
viagra 100mg online price in india
How to assess mathematics homework https://google.ci/url?q=https://buyessayreviews.com/essaypro-com/
Professional letter writing site for mba https://google.co.nz/url?q=https://buyessayreviews.com/essaytyper-com-review/
Help writing reflective essay on founding fathers http://maps.google.co.mz/url?q=https://buyessayreviews.com/studybay-com/
How to write a contract to rent a house https://www.lynlee.co.uk/reference-educationk-12-education-2/how-to-cite-a-poem-in-apa/
10g rac resume http://zfanta.weehan.com/board/3927915
Type my professional presentation online EssayPro
Pay for my cheap descriptive essay on lincoln Аuthor24
where to buy cialis for women
Essay plot https://notados.com/sophiashockley/compare-and-contrast-essay-introduction-sample/
tadalafil 20mg cost
Gattaca essays http://www-essaypro-com.ampblogs.com/Essaypro-discount-code-Essaypro-ae-Essaypro-end-contract-Essaypro-coupons-Sign-up-for-essaypro-44122208
brand name cialis online
Personal and professional achievements essay https://www.epubli.de/shop/buch/45209/go?link=https://papershelps.org
Against buffalo class dismissed essay including political politics whats wrong https://social-lyft.com/story605930/my-essaypro-essaypro-com-scam-essay-pro-com-essaypro-legit-log-into-essaypro
Make detailed outline research paper https://www-essaypro-com.popup-blog.com/11145213/essaypro-gay-essaypro-vs-using-essaypro-essaypro-writing-contest-essaypro-safe
Best mba content ideas http://byte-szr.ru/bitrix/rk.php?goto=https://buyessayreviews.com/studybay-com/
How to write your accomplishment charts https://xn--80abjdxyg2b.xn--p1ai/chat/thesis-statement-on-gun-control/
Cover letter name unknown http://norikae.jakushou.com/cgi-bin/mt4i221/mt4i.cgi?id=1&mode=redirect&no=2&ref_eid=50&url=https://buyessayreviews.com/essaypro-com/
cafergot tablets buy online
cost of ivermectin
Fashion designer resume objective examples http://maps.google.mu/url?q=https://buyessayreviews.com/studybay-com/
Bu accelerated program essay http://homex.ru/bitrix/rk.php?goto=https://buyessayreviews.com/essaypro-com/
Aids research paper introduction http://mimag.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://buyessayreviews.com/studybay-com/
where can i buy cialis tablets
Model sample resume http://google.ps/url?q=https://buyessayreviews.com/essaypro-com/
glucophage cost india
lyrica tablets 50mg
drug flomax generic
tetracycline tablets 500mg
celebrex 100mg mexico
celebrex.com
order tizanidine online
buy viagra europe
trazodone 150
ivermectin virus
diflucan rx online
ivermectin medicine
prinivil lisinopril
viagra gel australia
stromectol for humans
cialis online prescription usa
tadalafil best online pharmacy
ivermectin covid
lyrica from canadian pharmacy
Resume for police dispatcher sample https://championsleage.review/wiki/How_essaytypercom_will_help_you_get_an_essay_written_quickly
Rotman mba essay questions 2013 https://drive.google.com/file/d/1fJwiBpY9B1YL5fAHuh_Plk4fj8JTpqmP/view
Pay to write algebra admission paper http://s-tehno.ru/bitrix/rk.php?goto=https://buyessayreviews.com/essaypro-com/
Essays in ottoman and turkish history http://images.google.us/url?q=https://buyessayreviews.com
Cheap content ghostwriters service au https://www.blurb.com/user/boltorder3
John eby niles mi resume https://ccm.net/profile/user/picklelumber3
Free space optical communication thesis http://champagne-roederer.us/__media__/js/netsoltrademark.php?d=papershelps.org
Ib english extended essay rubric http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/1688238
Cover letter template job posting https://images.google.sn/url?q=https://bestessayservicereview.com/writepaperfor-me-review/
Birgit dopfer thesis http://dartlogistics.net/__media__/js/netsoltrademark.php?d=papershelps.org
cheap cialis 20mg australia
viagra 5mg price
viagra for sale mexico
order amoxicillin from canada
stromectol covid
diflucan tablets for sale
drug fluoxetine
price of tadalafil 5 mg
buy sildenafil
cheapest cialis
gkalpkutlu1 57rabia57 mehmetyasaryaar 5704ademkaya mehmetzyurt9 59ender
prazosin 10 mg
celebrex 209 mg
merhabaulkem 08glnihat 07_sevenn 07_nvz 07elmali 0758muhammet
doxycycline cost
vermox online usa
vermox buy online uk
medrol price
doxycycline online without prescription
canadian pharmacy no rx needed
where to buy xenical in australia
gabapentin 400 mg
price of generic effexor
tadalafil 20mg no prescription
viagra pfizer price
female viagra buy online in india
Write my best university essay on donald trump http://ezproxy.cityu.edu.hk/login?url=https://bestessayservicereview.com/essaytyper-com-review/
Pre testing questionnaire research paper http://www.bbs.91tata.com/home.php?mod=space&uid=11412324
Are college papers double or single spaced https://www.google.ee/url?q=https://papershelps.org
Car showroom business plan https://drive.google.com/file/d/1YmV0CInm3oddjNNdzqQ44Oeq3vuOzZwf/view
Professional presentation writers site for masters https://www.fcc.gov/fcc-bin/bye?https://bestessayservicereview.com/essaytyper-com-review/
cealis
Custom mba admission paper examples http://housetools.com.ua/bitrix/redirect.php?event1=&event2=&event3=&goto=https://essaytyper.cm/
Sat essay scale http://maps.google.com.bh/url?q=https://buyessayreviews.com/studybay-com/
Free debating essays https://athemes.ru/go?https://bestessayservicereview.com/writepaperfor-me-review/
How to write efficient c code https://www.google.sn/url?q=https://buyessayreviews.com/essaytyper-com-review/
Best cover letter proofreading sites for university http://dmfandassociates.com/searchpoint/redir.asp?reg_id=ptypes&sname=/searchpoint/search.asp&lid=1&sponsor=inc&url=https://essaytyper.cm/
Sample introduction for thesis chapter 2 http://greeksubtitlesproject.com/__media__/js/netsoltrademark.php?d=papershelps.org
You write my paper http://btb.club/space-uid-125805.html
Custom essays editor for hire online http://bisnews.co.th/__media__/js/netsoltrademark.php?d=essaypro.me
Should an essay title be in quotes https://essaywritingservicereviews.like-blogs.com/9928275/is-essaypro-com-the-top-essay-writing-service-review-of-my-experience
Give me a thesis title studybay
Cheap dissertation writers websites us http://www.jwwab.com/index.php?qa=user&qa_1=truckroad97
Alfie kohn article on homework https://www.bleckt.com/bitrix/redirect.php?event1=&event2=&event3=&goto=https://papershelps.org
Electronic thesis download http://www.mastermason.com/makandalodge434/guestbook/go.php?url=https://papershelps.org
What is a non-thesis degree program http://vortac.com/__media__/js/netsoltrademark.php?d=papershelps.org
viagra online america
Content graphic design resume http://zfanta.weehan.com/board/3877853
Linux trainer resume http://arctic-union.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://essaypro.me/
cialis 2.5 mg online
viagra for sale from canada
Esl dissertation chapter editing service for mba https://dokuwiki.stream/wiki/EssayPro_com_Essay_Publishing_The_best_dissertation_services_of_2022
cialis 20 mg lowest price
Business plan 4l trophy https://drive.google.com/file/d/1BVhWCyPVlInfhzdB3KfmZUeMI-7JSAzv/view
Nursing travel assignments https://gamegiraffe.com/members/fearangle4/activity/404075/
Professional cover letter editor website for university http://cikolatatadindasorular.com/index.php?qa=user&qa_1=hookstudy54
World order sample essays https://m.lmstn.ru/bitrix/redirect.php?goto=https://papershelps.org
tadalafil pills canada
Essay practice for ielts https://tinyurl.com/ycw2sb9g
Spanish voice over resume https://rylanenft62059.pennywiki.com/2558060/essaypro_com_is_the_best_essay_writing_company_review_of_my_experiences
cialis cream
tadalafil best online pharmacy
Writing good software engineering research papers shaw http://twitter.com/home?status=http://xurl.es/3owpw
Esl admission essay writer service ca https://notes.io/qqbTw
modafinil 50mg
prozac 20 coupon
Essay houses dorms http://ijfisnar.info/__media__/js/netsoltrademark.php?d=papershelps.org
Professional descriptive essay writers website for school https://avfocus.avclub.pro/bitrix/redirect.php?event1=news_out&event2=http2F2FADnh-sA1ch-bA1n-hA0ng-chung-cB0-vincity-ocean-park-tBBA7-91D0D0D1D1%84B582B0&goto=https://papershelps.org
Dissertation ghostwriters service uk http://soal-jawab.com/index.php?qa=user&qa_1=thrillbeetle37
finasteride cost
Senior it consultant resume https://www.cakeresume.com/me/heightrotate0/
Buy art & architecture paper https://www.elzse.com/user/profile/358874
Oracle programmer resume sample http://926gm.com/home.php?mod=space&uid=149591
legit non prescription pharmacies
Toefl writing essay structure http://www.drugoffice.gov.hk/gb/unigb/bestessayservicereview.com
Termpaper about implementation of public policy http://karlcraft.com/__media__/js/netsoltrademark.php?d=papershelps.org
Cheap application letter ghostwriter website for phd http://liumeiti.top/home.php?mod=space&uid=2426579
Research report writting https://google.co.hu/url?q=https://buyessayreviews.com/essaytyper-com-review/
Sebastian glende dissertation https://gillespie-tan.technetbloggers.de/is-essaytyper-an-ad-hominem-scam-or-is-it-a-legitimate-and-legal-method-to-obtain-free-college-essay
Resume templates microsoft word download http://www.bsrrealty.com/SearchPoint/redir.asp?reg_id=pTypes&sname=/searchpoint/search.asp&lid=2&sponsor=COM&url=https://essaypro.me/
cost for valtrex
online pharmacy group
ventolin over the counter canada
paxil brand name cost
anafranil 10 mg
buy anafranil
cost amoxicillin 875 mg
order clomid from canada
disulfiram 500
ivermectin cream cost
genuine clomid online
can you buy ventolin over the counter nz
clomid for sale uk
generic for retin a
fildena 200mg
how much is prednisone 5mg
ivermectin lotion for scabies
antabuse price in india
where can i buy viagra over the counter canada
buy cialis over the counter canada
medicine neurontin
albendazole in usa
diflucan rx price
amoxicillin 500 mg tablets
where to buy real viagra cheap
combivent respimat cost
metformin 500 price india
glucophage drug
bactrim in mexico
augmentin uk price
sildalis 120 mg order canadian pharmacy
600 mg gabapentin cost
tizanidine 4 mg capsule coupon
buy generic valtrex online canada
flomax for ed
clomid in australia
vermox over the counter canada
How to write a letter to a teacher of english http://www.xn--hq1b37iutl0qb06cj1iura767c.kr/qna/1540191
I need help making a thesis https://whatisnewstoday.com/forums/users/incomesmell52/
How to write a manuscript review https://service.affilicon.net/compatibility/hop?hop=dyn&desturl=https://bestessayservicereview.com/writepaperfor-me-review/
Columbia appel fellowship essay https://maps.google.com.bd/url?q=https://bestessayservicereview.com
Popular masters book review sample http://stark-indu.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://bestessayservicereview.com/
January 2010 essay prompt sat http://y4yy.com/index.php?qa=user&qa_1=faucetwave45
Free classfication essay http://www.giant.org.cn/space-uid-310437.html
Ex of resume EssayPro
Esl personal essay writing website us http://georgievsk.ru/bitrix/rk.php?goto=https://essaypro.me/
Brenda pauly lapd cv resume https://vimeo.com/magicpepper6
Common app essay work experience http://www.xibeiwujin.com/home.php?mod=space&uid=1466154
Masters degree program acceptance request essay http://maps.google.at/url?q=https://buyessayreviews.com/studybay-com/
Free resume format for co ordinator https://zzb.bz/0xVRw
Harry potter and the sorcerer39s stone essay topics http://psnfusion.com/content/index.php?option=com_k2&view=itemlist&task=user&id=1743029
albuterol 4mg
Resume fillout https://maps.google.com.cu/url?q=https://buyessayreviews.com/studybay-com/
Patent law research paper topics http://qooh.me/graingrip63
Cool graphic artist resume https://hikvisiondb.webcam/wiki/EssayProcom_Essay_Posting_The_best_article_services_of_2022
Research paper course outline https://drive.google.com/file/d/1jXSuzuBajjXsBrZZmWlRtwZVQDp00ZkU/view
Essay on dr abdul kalam azad https://shareapet.org/volunteer3/?unapproved=183607&moderation-hash=a6e178cd41f03690101e632b2e0548e9
Professional writer http://northstarshoes.com/europe/out.php?url=https://buyessayreviews.com/
Homework amswers http://rokenterprisesinc.com/__media__/js/netsoltrademark.php?d=papershelps.org
Essay for grade 8 https://www.wattpad.com/user/areacopper1
Hemingway’s memoir essays https://motogpdb.racing/wiki/Essay_Bot_Reviews_2022_UPDATED_Are_Essay_Bots_Legal_or_Scam
Sample resume format for mba marketing https://test.ezmobile.pl/bez-rubriki/paydayplus-net-payday-loans-review-2022/
Sgu interview essay questions http://www.jwwab.com/index.php?qa=user&qa_1=cameraeffect51
Cover letter company specific https://maps.google.com.uy/url?q=https://bestessayservicereview.com/writepaperfor-me-review/
celebrex comparison
Popular expository essay proofreading websites for masters https://rokslides.com/how-do-you-write-a-cursive-i/
Death penalty should not be abolished essay https://www.gaibandhahelpline.com/uncategorized/910900/
Cheap assignment writer site for phd https://fanslations.azurewebsites.net/release/out/death-march-kara-hajimaru-isekai-kyousoukyoku-9-32/5628/?url=https://bestessayservicereview.com/writepaperfor-me-review/
Essay on being in trouble https://drive.google.com/file/d/14C-1JIFN86ugeHn7OOiQ-O05buOdX4hD/view
Van gogh mental illness essay https://maps.google.it/url?q=https://buyessayreviews.com/studybay-com/
Dissertation proposal writers for hire http://newtonpowell.com/__media__/js/netsoltrademark.php?d=papershelps.org
Morgan rowe decatur ga resume https://jaredjykv90999.eveowiki.com/9741206/essaypro_com_is_the_top_essay_writing_company_review_of_my_experiences
buy levitra online no prescription
Patterns of resume writing https://cameradb.review/wiki/EssayPro_com_Essay_Composing_The_best_composition_writing_services_of_2022
Resume cover letter samples sales manager https://pinshape.com/users/2235507-attacktempo59
Belonging essay 2 related texts https://maps.google.dz/url?q=https://buyessayreviews.com/essaypro-com/
How ro write a dateing profile https://docs.google.com/document/d/15UB-VksixP1KdhQ9baPtC8D4zKXN9Kiz8WisepSVtSQ/edit
Custom movie review editing for hire for phd https://www.kickstarter.com/profile/1533975062/about
Popular mba essay proofreading sites online https://anotepad.com/notes/bcmjg85s
Business plan for dry cleaning and laundry https://historydb.date/wiki/Is_EssayTyper_legal_or_fraudulent
Esl assignment editor service usa spotlian
generic trazodone 50 mg
Buy music dissertation hypothesis http://www.salesmanager.co.kr/question/2272601
Uc personal statement prompt http://wordoid.in/essay-writing-services-mongolia-essay-writing-services-mongolia/
Cheap creative writing ghostwriter sites gb https://livebookmark.stream/story.php?title=the-most-effective-essay-writing-solutions-of-2022#discuss
Popular paper ghostwriters sites uk https://moftree.cn/home.php?mod=space&uid=109525
Custom expository essay writer service for college http://images.google.at/url?q=https://bestessayservicereview.com
Business plan for training and development company http://eshopee.cn/space-uid-115389.html
Sample essays on paintings http://couponwhisper.com/members/topsong8/activity/553304/
Rhetorical analysis essay editor sites au http://www.lawrence.com/users/hoewhite66/
Leapor an essay on http://borsafix.com/index.php?qa=user&qa_1=sphereotter29
Essay motivation mba http://eng.prokatavtomobil.by/user/jutebrass4/
Esl bibliography ghostwriting services for masters http://www.komus-opt.ru/bitrix/rk.php?goto=https://buyessayreviews.com/essaypro-com/
How to teach writing book reports https://google.com.nf/url?q=https://buyessayreviews.com/essaypro-com/
Resume sample for nurse aide https://marvelvsdc.faith/wiki/StudyBay_Review_for_2022_Scam_or_legitimate_Service
Address cover letter to director of human resources https://lexsrv3.nlm.nih.gov/fdse/search/search.pl?match=0&realm=all&terms=https://buyessayreviews.com/studybay-com/
Bedford engineering homework mechanics statics http://webhannetgc.com/__media__/js/netsoltrademark.php?d=papershelps.org
Freedom definition essay http://guangzhou-ru.com/home.php?mod=space&uid=106543
Sample cover letter for fresh graduates hotel and restaurant management https://troypcoy00999.bloggerchest.com/9724999/essay-pro-usa-essaypro-writing-contest-scholarship-essaypro-writing-essaypro-tutor-essaypro-promo-code
Writing service in newark nj http://russian-poster.ru/bitrix/rk.php?goto=https://buyessayreviews.com/essaytyper-com-review/
Homework solutions physics for scientists and engineers http://www.badboyzchoppers.net/__media__/js/netsoltrademark.php?d=papershelps.org
Cheap papers writing site gb http://google.bi/url?q=https://bestessayservicereview.com/writepaperfor-me-review/
War photographer essay https://painless.network/members/texthandle14/activity/763223/
High school essay introduction examples https://thengisa24.com/user/profile/264900
How to write an sba business plan https://akademi.skor77.com/members/heliumvoyage60/activity/414204/
Accounting dissertations titles http://esptools.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://buyessayreviews.com/studybay-com/
Best practices for teaching essay writing studybay
Top creative essay writers for hire au https://wiki.changeringing.co.uk/index.php?title=%2Fpapershelps.org&action=edit&printable=yes
Popular essay proofreading services for college CashNetUsa
Popular application letter ghostwriter for hire for university https://fabnews.faith/wiki/Best_Essay_Writing_Services_Get_Your_Essay_Done_Right
Higher order concerns academic writing http://hawkee.com/profile/1465151/
How to write a cursive d http://koyomi.vis.ne.jp/wiki/index.php?layerborder53
Chemistry extended essays ib https://xueyunwei.com/home.php?mod=space&uid=329503
Cheap dissertation abstract ghostwriting service for mba http://hiegogroup.com/bbs/home.php?mod=space&uid=847510
Paralegal essay topics http://atlastower.com/__media__/js/netsoltrademark.php?d=papershelps.org
How to write jsp in web xml http://altorsc.com/__media__/js/netsoltrademark.php?d=papershelps.org
Stem cells research newspaper article http://tools-world.ru/bitrix/rk.php?goto=https://essaypro.me/
Professional course work proofreading service for college http://ipcapi.net/__media__/js/netsoltrademark.php?d=papershelps.org
Essay on passivity https://drive.google.com/file/d/1zqfomMT7bGLZ62UacFA4_mZQQiIl5L62/view
Sample resume objective for housekeeper http://www.lawrence.com/users/penbabies0/
Esl essay ghostwriters for hire us https://myemotion.faith/wiki/Why_essayusacom_is_the_most_effective_essay_writing_service_for_students
Writing assignments 6th grade http://y4yy.com/index.php?qa=user&qa_1=heavendust5
Popular expository essay editing services for university http://italyspeciality.com/__media__/js/netsoltrademark.php?d=papershelps.org
Senior research fellow resume http://www.weidaoo.com/home.php?mod=space&uid=538885
Cgi how to write to user specified location http://maltafawuq.net/index.php?qa=user&qa_1=peppertrain54
School library assistant resume sample https://sunnylivingflorida.com/citing-a-poem-in-apa-2022/
Reflective writer sites online http://2etechnologygroup.com/__media__/js/netsoltrademark.php?d=papershelps.org
How to write a business bio https://images.google.rw/url?q=https://buyessayreviews.com
Asset dissertation empirical investigation liquidity pricing https://historydb.date/wiki/Is_EssayTyper_a_fraud_or_an_authorized_way_to_get_free_college_essays
Rubric for how to essay https://www.mixcloud.com/willowtrail3/
Research paper about customs administration https://tiu.ru/redirect?url=https://papershelps.org
Esl thesis proofreading service for phd https://prolightroom.justclick.ru/lms/api-login/?_hash=ZR3ey6/M1V6D9BkZe0rtENxgkabOUzxg1Qt8FRlgglk=&authBhvr=1&email=-f8rsi3iilingyr13d3qcnb54&expire=1577061050&lms=0&targetPath=https://papershelps.org
Examples of broad and narrow thesis statements http://pandora.nla.gov.au/external.html?link=https://bestessayservicereview.com
Master dissertation sample pdf http://foreverygirl.info/__media__/js/netsoltrademark.php?d=papershelps.org
Popular descriptive essay writing for hire us https://arqma.smartcoinpool.net/question/606507/what-to-title-an-essay-2022/
Esl book review editing for hire usa https://www.fcc.gov/fcc-bin/bye?https://essaytyper.cm
Essay on my favourite teacher in marathi http://mediball.hu/members/saleheron15/activity/605240/
Custom cheap essay editor for hire au http://paxiaojie006.xyz/home.php?mod=space&uid=602387
Best critical essay editor site for school https://gemsfly.in/members/gunnerve39/activity/756210/
Thesis statement outline compare contrast essay http://www.google.com.pr/url?q=https://buyessayreviews.com/essaytyper-com-review/
Dabbawala business plan https://www.hostsuche.de/aklick.php?id=529&siteurl=https://papershelps.org
Culinary resume objective statement http://www.imruyi.com/space-uid-320748.html
Variationadaptation essay https://chanceopkv47269.wikihearsay.com/1290645/essaypro_com_is_the_top_essay_writing_service_review_of_my_experience
Custom definition essay editor for hire online https://images.google.de/url?q=https://buyessayreviews.com/studybay-com/
Hamlets essay revenge http://ipv4.google.com/url?q=https%3A%2F%2Fwww.essaypro.me%2F
1 page template business plan http://www.adaxes.com/questions/index.php?qa=user&qa_1=horsejapan9
Custom term paper ghostwriter site for masters http://tysonjxir77662.bloggin-ads.com/31196880/essaypro-plagiarism-essaypro-blog-how-to-write-a-thesis-statement-essaypro-essaypro-com-essay-pro-uk-essaypro-uk
Write my trigonometry admission essay http://virtuoso.openlifedata.org/describe/?url=https://buyessayreviews.com/studybay-com/
Popular resume writing website usa https://thengisa24.com/user/profile/241248
Resume lines for cashier https://xiaozhizhen.com/home.php?mod=space&uid=128048
Professional thesis ghostwriting services for mba https://docs.google.com/document/d/1aOtYTp_l0nEbM9EWY_QPYwkiO0LjHzKPvRSgWni2_P0/edit
Help with popular school essay on civil war https://essaypro-com.theblogfairy.com/11149418/essay-pro-com-essaypro-instagram-essaypro-facebook-essaypro-owner-essaypro-usa
Top argumentative essay editing service online https://linkgeanie.com/profile/flaxdecade72
Joseph addison essay on ghosts and apparitions https://drive.google.com/file/d/154soEZLmeDoZYoOMd7WyBwHh5w-dY4YK/view
Free igcse coursework ict analysis http://vsevteme.ru/problems/new?back=https://essaytyper.cm/
Blood is thicker than water short essay https://cse.google.cv/url?q=https://bestessayservicereview.com/writepaperfor-me-review/
How to write intriguing male and female characters https://pastelink.net/0fljirbh
Юридическая помощь по любым правовым вопросам. Консультация по телефону бесплатно.
Звоните в любой день: +7 (495) 128-55-69
Custom annotated bibliography writer sites us http://tsxxue.com/index.php?qa=user&qa_1=elbowrail25
Common mistakes in ielts essay writing http://kawaii-writing.com/__media__/js/netsoltrademark.php?d=papershelps.org
Popular mba literature review advice https://drive.google.com/file/d/1N7Ixft7WUPA7vM1YVUOvBxYs8UCglyi7/view
Я – частный компьютерный мастер. Занимаюсь ремонтом компьютеров и ноутбуков с выездом на дом.
Компьютерная помощь любой сложности.
Работаю без выходных и праздников.
Звоните в любой день и в любое время: +7 (995) 577-67-35
Ucsd thesis template http://zaday-vopros.ru/index.php?qa=user&qa_1=litterrocket83
Best curriculum vitae writing websites for masters https://www.sante-dz.org/doc.php?url=https://papershelps.org
Financial data restaurant business plan https://championsleage.review/wiki/StudyBay_Reviews_for_2022_Scam_or_legitimate_Service
Top bibliography writer website for university https://drive.google.com/file/d/1ikB-AicTu19ZRRKGFa0v3Z7hHK72LCYF/view
Psychology paper topics autism https://www.google.com.pl/url?q=https://buyessayreviews.com/essaytyper-com-review/
How to write official response letter http://google.co.vi/url?q=https://buyessayreviews.com/studybay-com/
Available master thesis in digital design http://spenceriylj49667.canariblogs.com/essaypro-account-customization-essay-pro-phone-number-essaypro-youtube-essaypro-us-login-essaypro-phone-number-24237165
Type my finance case study http://tsxxue.com/index.php?qa=user&qa_1=looksun0
Rules of a good resume http://m.ok.ru/dk?st.cmd=outLinkWarning&st.rfn=https%3A%2F%2Fwww.essaypro.me
Cover letter examples medicine https://moftree.cn/home.php?mod=space&uid=91611
Biology a2 coursework help https://google.ee/url?q=https://buyessayreviews.com/essaytyper-com-review/
Free modern dance research paper lending bear
Steps for writing a qualitative research paper https://marvelvsdc.faith/wiki/StudyBay_review_for_2022_Scam_or_legitimate_Service
How to write a good ad analysis essay https://picktocar.com/index.php?page=user&action=pub_profile&id=117624
Business plan ghostwriting site http://www.mmdbw.com/space-uid-243108.html
Replace the resume objective with a personal brand statement https://www.cookprocessor.com/members/garagepeen4/activity/1614083/
Top biography editing services for university https://joeclassifieds.com/index.php?page=user&action=pub_profile&id=2099416
Professional dissertation abstract writers sites for phd http://borsafix.com/index.php?qa=user&qa_1=queenbelt88
Selfishness essays https://ads.massagemehomeservices.com/index.php?page=user&action=pub_profile&id=2257406
Staple a 2 page resume http://www.aerogel.co.nz/__media__/js/netsoltrademark.php?d=papershelps.org
Thesis islamic banking pdf http://google.cz/url?q=https://bestessayservicereview.com
Scarface 1983 articles essays https://myemotion.faith/wiki/Is_EssayTyper_an_ad_hominem_scam_or_is_it_an_authentic_and_legal_way_to_get_free_college_essays
How to write a business proposal for an ngo http://www.docspal.com/viewer?id=drdrgkwd-20816355
Essay search engine com https://maps.google.co.nz/url?q=https://buyessayreviews.com
Descriptive essays about nightmares https://farrag-group.com/community/profile/chasecamden4873/
Secrecy essay on frankenstein https://drive.google.com/file/d/10FthdodXQ18IAlIeDbmHpdywihKTL8Fa/view
Term papers outsourcing https://schoolhouseteachers.com/dap/a/?p=https://papershelps.org
Fuzzy thesis http://freseniusvascular.net/__media__/js/netsoltrademark.php?d=papershelps.org
Top bibliography editing services us http://www.imruyi.com/space-uid-320748.html
Popular assignment editor services usa http://emseyi.com/index.php?qa=user&qa_1=backdoor5
University editing websites gb http://0123zx.com/home.php?mod=space&uid=287850
Audison thesis uno price http://druzhba5.dacha.me/user/babiescalf6/
Custom book review ghostwriters website for phd https://drive.google.com/file/d/1CpV_bJVdFvrSe2JChgehfm6rMgNHhN_c/view
Essay on status of women in today’s society https://coderwall.com/p/ba_g3g/is-essaytyper-fraud-or-is-it-a-legit-and-legal-method-to-obtain-free-college-essays
Applying for management position cover letter http://www.google.co.hu/url?q=https://buyessayreviews.com/essaytyper-com-review/
Popular movie review editing sites for phd https://weixing13.com/home.php?mod=space&uid=245439
English argumentative essay format http://tork-club.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://essaytyper.cm/
Help me write shakespeare studies article review https://www.hulkshare.com/pintbrian90
Popular dissertation chapter writer websites gb https://www.4shared.com/office/kSq-K0Gpea/What_is_the_reason_why_essayus.html
Attorney associate cover letter http://y8space.com/members-2/trickcoin10/activity/2198371/
Problem solving editor service au https://www.google.com.au/url?q=https://buyessayreviews.com/essaypro-com/
Book publishing process https://xn--80abjdxyg2b.xn--p1ai/chat/process-essay-samples-2022/
Canadian sovereignty essay https://phonographic.science/wiki/StudyBay_Reviews_for_2022_Scam_or_legitimate_Service
Free random essays https://www.inventables.com/users/havewinther5190
Resume family law attorney https://vimeo.com/frowntaurus2
Essay detailed structure https://www.google.nr/url?q=https://bestessayservicereview.com/writepaperfor-me-review/
Gre writing percentile 2017 http://konectacasa.com/index.php?page=user&action=pub_profile&id=371420
Esl creative essay writer site us https://drive.google.com/file/d/1iT_7RqbDYV_EnTp3xhGv83vdKXEc6MjK/view
Essay in life sign usa https://www.gufenghanfu.com/space-uid-215453.html
Noahs ark essay http://linksus.zhugeio.com/v2/adtrack/c/931318990bad40019d489cbec27271e9/pr0002/m00004/p4001/c0?url=https://papershelps.org
Cause or effect essay sample https://bbs.pku.edu.cn/v2/jump-to.php?url=https://controlc.com/8353e9b8
Write u.S. History and government essays http://giftsmarts.com/__media__/js/netsoltrademark.php?d=papershelps.org
Best movie review writer services uk http://musicmen-dv.ru/bitrix/redirect.php?event1=&event2=&event3=&goto=https://buyessayreviews.com
Essays form interpretation https://drive.google.com/file/d/1LX3CUMoVTCjwwowmxGbLaDgl2LqsHpp2/view
Random philosophy essay generator http://www.livecmc.com/?lang=fr&id=Ld9efT&url=https://buyessayreviews.com/essaytyper-com-review/
Professional research proposal writing for hire au http://www.xueba.city/home.php?mod=space&uid=219643
Type my education curriculum vitae https://maps.google.com.gh/url?q=https://buyessayreviews.com/essaytyper-com-review/
Primary functional expertise resume examples http://www.google.com.sl/url?q=https://buyessayreviews.com/essaytyper-com-review/
Top reflective essay ghostwriters site for mba https://gemsfly.in/members/belllibra75/activity/746019/
Essay street crimes in pakistan http://vipersrc.com/home.php?mod=space&uid=58031
College essay admission heading https://google.nl/url?q=https://buyessayreviews.com/studybay-com/
Literature review on mobile banking http://www.birthdoula.com/__media__/js/netsoltrademark.php?d=papershelps.org
Pay for my esl expository essay on civil war http://rateyourmix.com/members/cokefreeze6/activity/473087/
How to write a bibliography worksheet http://zgtxcc.com/space-uid-291291.html
Best dissertation chapter editing services uk http://www.linkagogo.com/go/To?url=112580469
Coursework regulations for undergraduate programmes https://drive.google.com/file/d/18rB2qvYOLwUWRLK_mQljMlNgoR0_OIhb/view
Title page apa style template https://historydb.date/wiki/Honest_PaperHelp_Review_PaperHelporg_Review_Is_PaperHelporg_Legit_Safe
Sample quantitative research proposal pdf https://www.indiegogo.com/individuals/29225366/
Example of apa format of reference http://studyinla.cn/home.php?mod=space&uid=102627
Popular dissertation abstract ghostwriting for hire https://maps.google.hu/url?q=https://bestessayservicereview.com
Sir george savile king charles ii essay http://www.phishtank.com/
Custom dissertation results ghostwriters for hire us http://rateyourmix.com/members/coltgender4/activity/474337/
Bibliography ghostwriting for hire uk http://brewwiki.win/wiki/Post:Best_Essay_Writing_Services_Reviews
Esl case study ghostwriter services for mba http://nikolab.ru/links.php?go=https://buyessayreviews.com/essaytyper-com-review/
Describe your favorite teacher essay http://www.megavideomerlino.com/albatros/torneo/2010101617spadafora/default.asp?inl=0&lin=9030
Literary analysis essay winter dreams http://dbdxjjw.com/Go.asp?url=https://papershelps.org
Professional biography ghostwriters for hire usa https://johsocial.com/story611321/essaypro-review
Popular annotated bibliography writing website for masters https://www.52miaomu.com/space-uid-281105.html
Resume samples for computer skills https://scientific-programs.science/wiki/How_essaytypercom_can_assist_you_in_getting_your_essay_completed_in_a_short_time
Order ecology paper https://immaster.ru/good-topics-for-a-narrative-essay/
Conference director resume http://www.google.com.cu/url?q=https://bestessayservicereview.com
Professional critical essay writers for hire ca http://alra7al.net/index.php?qa=user&qa_1=neckneck8
Professional school argumentative essay ideas https://www.kliniekonline.nl/lending-bear-payday-loans-review-2022/
Professional admission essay ghostwriting site for mba http://dongku.org/space-uid-1519530.html
Classification and comparison contrast essay http://support.zenoscommander.com/index.php?qa=user&qa_1=lowcotton47
World’s first dimensionless bluetooth rings https://project-br.com/ smart electronics, smart adapter, wearable electronics system, designer jewelry brand names, power bank wireless, power bank recommended, power bank universal, power bank iphone 12, power bank station
Nicely put, Kudos. custom writing english writing essay
where can i buy flomax
where to get clindamycin
cost of bupropion
lexapro 30 mg
colchicine online canada
generic cialis for sale
augmentin 325 mg
valtrex medication cost
generic kamagra jelly
cost of prozac without a prescription
propecia 2016
where to get viagra online
best viagra capsule
cheap ciprofloxacin 500mg
deltasone 10 mg
escrow pharmacy online
stromectol prices
buy accutane 20mg
provigil 100mg price
where can i get keflex
finasteride propecia
bactrim mexico
online pharmacy 365 pills
bactrim 168 mg
buy provigil online with mastercard
20mg sildenafil online prescription
buy disulfiram without prescription
ventolin cost uk
roche accutane without prescription
cipro for sale online
wellbutrin 2019
which pharmacy is cheaper
levaquin online
doxycycline 75 mg coupon
order priligy online uk
motrin 600 mg over the counter
modafinil buy online nz
bupropion 150 mg no prescription
buy amoxicillin 875 mg online
erectafil 20
best european online pharmacy
plavix 40 mg tablets
diflucan in usa
propranolol otc canada
how much is voltaren tablets
hydroxychloroquine sulfate
augmentin xr
where can i get paxil
buy cheap nolvadex online without prescription
medrol 4mg pak
modafinil online pharmacy
augmentin online canada
clopidogrel pharmacy
atarax 25 mg over the counter
buy lyrica 300mg
tretinoin cream price india
nolvadex prescription
nolvadex india price
doxycycline 200 mg daily
suhagra 100 online
citalopram hbr tabs
can you buy atarax over the counter
buy diflucan 150mg
cheap prednisolone tablets
prednisolone online uk
lopressor 100
uk pharmacy no prescription
singulair cost canada
cost of seroquel 25 mg
legitimate mexican pharmacy online
effexor xr 75
ciprofloxacin 250 mg tabs
citalopram 40mg brand name
bupropion 100 mg
generic of yasmin
best brand metformin
cytotec 0.8 mg daily
nolvadex without prescription
prednisolone uk buy
1700 mg metformin
cost of advair in mexico
order prozac online uk
lipitor tablets price
fluoxetine hydrochloride
diflucan drug
generic tamoxifen
dapoxetine online uk
buy flagyl no rx
avana 31311
viagra canada
metformin where to buy
cleocin cream acne
propecia gel
generic advair diskus canada
buy propecia uk online
generic for cipralex
modafinil prescription usa
prozac australia
cleocin 150 cost
tretinoin capsule
lisinopril 40 mg mexico
retino 0.25 cream price
provigil buy usa
phenergan over the counter in uk
priligy cost
happy family store pharmacy
anafranil anxiety
albendazole online uk
clomid over the counter uk
accutane vitamin a
clindamycin for sale
order fluconazol
azithromycin 250mg tablets for sale
generic abilify 2mg
alli orlistat 60mg
retin a gel purchase
accutane canada cost
motrin
best over the counter clomid
abilify 100mg
diclofenac united states
celexa rx
can you buy phenergan over the counter
online singulair
how much is wellbutrin
accutane singapore cost
cost of generic benicar
legitimate canadian pharmacies
safe online pharmacies
canadian pharmacy without prescription
diflucan 150 cost
online pharmacy indonesia
gabapentin 300 capsule
dipyridamole capsules 200mg
disulfiram for sale
canadian world pharmacy
doxycycline 100 mg capsule
can you buy amoxicillin online uk
buy lasix online
cheap viagra online united states
canadian pharmacy ltd
buy antabuse tablets uk
buy lasix without presciption
1000 mg valtrex cost
vardenafil hcl 20mg tab
buy accutane tablets
online pharmacy without scripts
augmentin 800 mg
levitra tablets in south africa
pharmacy home delivery
furosemide 40 mg cheap
colchicine generic brand
average cost of zoloft
budesonide discount
best rx pharmacy online
metformin tablets where to buy
acyclovir cost
buy fluconazol
prazosin depression
zovirax australia
order valtrex online canada
zoloft prescription
colchicine tablets
budesonide 0.5 mg
augmentin xr 1000
modafinil how to get prescription
order cialis daily
canadian family pharmacy
4800 mg gabapentin
dexamethasone 0.5 tablet
cephalexin brand name india
amoxicillin pills 500 mg
lisinopril 40 mg no prescription
buy azithromycin uk
prednisolone 20 mg
prednisolone price us
how to buy doxycycline
cialis 2.5 daily
how much is azithromycin 1g
buying from canadian pharmacies
methocarbamol robaxin
dexamethasone 8 mg tablet
cost for 40 mg lisinopril
generic cipro price
gabapentin online prescription
fildena 100 online
robaxin muscle relaxant
online pharmacy bc
where can you buy zithromax
innopran brand name
prednisolone brand name australia
propranolol 60 mg tablet
retin a over the counter
baclofen 20 mg
where to buy cipro online
canadian pharmacy no rx needed
erectafil 40 mg
buy malegra 50 mg
albuterol medicine in india
doxycycline prescription uk
order albendazole online
citalopram without prescription
canada pharmacy online
baclofen 4097
can i buy doxycycline over the counter in south africa
synthroid 88 brand prices
generic synthroid price
tadalafil 10mg price
where can i buy flomax
paroxetine online uk
motilium otc canada
albendazole online uk
erectafil 40 mg
erectafil 40 mg
citalopram hbr
malegra 200 mg price
price zovirax cream
buy generic levitra in usa
tamoxifen buy online
baclofen tabs
tretinoin 0.05 cost
buy provigil canada pharmacy
viagra best buy
fluoxetine 20 mg tablets price
celebrex 2016
cial
antabuse medication over the counter
augmentin online nz
vermox in canada
flomax 40
amoxicillin 100 mg
flomax nasal spray
prescription drug flomax
antabuse buy
indian pharmacy
tamoxifen 20 mg cost
cost of flomax in canada
amoxicillin 500 mg cost
can you buy zovirax cream over the counter
tizanidine 4mg tablets
motilium medication
atarax tablets
motilium 10mg
buy modafinil australia
diflucan otc
buspar 10 mg tablets
over the counter toradol
celebrex brand name
albendazole pills
fluoxetine 40mg prices
cialis 2.5 mg canada
buy diflucan 150mg
toradol cream
canada rx pharmacy world
diflucan otc usa
discount sildalis 120mg
cost of erythromycin in india
buying diflucan
toradol back pain
toradol 150 mg
all in one pharmacy
pharmacy online 365
ventolin 100
anafranil medication
albuterol 4mg
cheap priligy online
sky pharmacy
order dapoxetine online in usa
zoloft
where can you get toradol
dapoxetine australia price
ventolin 4mg uk
can you buy lyrica over the counter
erythromycin tablets
cheap xenical online
orlistat prescription online
price of toradol
dapoxetine 60mg in india
cheap modafinil tablets
toradol pill form
viagra singapore prescription
how to order valtrex online
advair diskus coupon
cost less pharmacy
dapoxetine generic uk
medicine tetracycline 500mg
flomax hypotension
prazosin cost uk
clopidogrel cost uk
effexor medication
medicine motilium 10mg
valtrex without insurance
ampicillin for sale
amitriptyline over the counter
terramycin antibiotic
lisinopril 5 mg canada
where can i buy azithromycin over the counter nz
albuterol price
cheapest pharmacy to get prescriptions filled
terramycin
cafergot
where can i buy generic flomax
sumycin price
zithromax generic cost
lisinopril 40 mg for sale
tetracycline tablets india
how much is gabapentin cost
generic propecia from canada
allopurinol no prescription
wellbutrin 100 mg tablet
trazodone uk prescription
gabapentin 400 mg capsule
kamagra jelly viagra gel sachets
kamagra oral jelly gumtree sydney
neurontin 3
buy cytotec online usa
propecia over the counter canada
strattera 40mg
cafergot 1 100 mg
100 mg lasix no prescription
prozac 40 mg tablets
orlistat an over-the-counter weight loss drug
cheap cymbalta online
how to get bactrim
paxil tablets in india
tamoxifen buy online
purchase trazodone online
cheap levitra 10 mg
prozac brand price
order synthroid from canada
60 mg prozac
terramycin ophthalmic ointment for dogs
buy cafergot
brand name allopurinol
order bactrim ds
script pharmacy
dexamethasone tablets 1.5 mg
bactrim 500 mg
phenergan 25mg nz
buy gabapentin online uk
1500mg bupropion
cost of lasix 10mg
order cymbalta
tetracycline cream over the counter
buy lisinopril no prescription
cost of brand name celexa
furosemide 40 mg tablet
buy kamagra eu
clopidogrel 75 mg price in india
baclofen 5 mg price
500 mg cipro
canadian pharmacy online store
misoprostol buy online us
kamagra oral jelly price in dubai
purchase orlistat
10mg baclofen
levitra over the counter
zithromax over the counter usa
diclofenac otc in usa
singulair canada
buy nolvadex tamoxifen citrate
average cost of buspar
cipro xl
gynecomastia nolvadex
cost of buspar
sildenafil soft tabs generic
cymbalta 150 mg
generic strattera online
can you buy azithromycin over the counter in canada
levitra tablet price in india
best gabapentin brand
how much is strattera medication
zovirax 500
kamagra oral jelly perth wa
lasix tablet price in india
azithromycin 500 mg tablet price
cost of neurontin
diclofenac brand name
trusted canadian pharmacy
citalopram coupon
tamoxifen tablets
safe canadian pharmacy
lasix with no prescription
cost of cymbalta 60 mg
albendazole 400mg tablet price
buy generic atenolol
propecia for sale
celebrex gel
silagra uk
order tetracycline without a prescription
biaxin 500 mg price
where can i buy elimite cream
biaxin pill
hydrochlorothiazide 25 mg tab tablet
atenolol cream
triamterene 50 mg
buy benicar
generic advair us
erectafil canada
synthroid prescription
malegra on line
triamterene 25 mg
trustworthy online pharmacy
citalopram insomnia
atenolol 25 mg tablet price in india
cost of advair in us
how to get tetracycline
tenormin 25 mg tab
phenergan over the counter australia
generic otc singulair
order antabuse no prescription
phenergan 25 mg tablets uk
diclofenac 75 mg cost
plavix uk
clopidogrel medicine
chloroquine coronavirus
lyrica 25mg capsule
lexapro 5mg
cephalexin cost uk
estrace cream price canada
acyclovir cost singapore
aralen generic
phenergan gel prescription
generic tadacip
buy retin a online without a prescription
aurogra 100
tadacip
atenolol otc
propranolol prescription cost
bactrim price south africa
levaquin 750
silagra 100mg from india
buy levitra generic
canada online pharmacy no prescription
arimidex cost uk
bactrim drug
generic sildalis
estrace online pharmacy
prednisolone 5mg prices
buy tamoxifen canada
tadacip 20 mg price
motilium tablets over the counter
chloroquine phosphate 500 mg tablet
lyrica 150 mg capsule
acyclovir online uk
order chloroquine phosphate
how to get zyban uk
order prednisone online no prescription
colchicine usa
benicar prescription prices
canada neurontin 100mg lowest price
buy flagyl without a prescription
buy stromectol uk
buy motrin 800
cymbalta 120 mg
how much is bactrim 800 mg
cost of keflex
canadian mail order pharmacy
propecia hair growth
digoxin 25 mcg
nolvadex 10mg price in india
paxil for children
budesonide 3 mg capsule cost
online pharmacy delivery
pharmacy online 365
robaxin drug
cephalexin antibiotic
bactrim 960
colchicine drug price
propecia over the counter canada
vermox 500
stromectol over the counter
bactrim over the counter uk
can you buy ampicillin over the counter
where can i buy bactrim over the counter
order ampicillin
azithromycin in canada
cymbalta 40 mg price
generic avodart from india
celebrex cost comparison
benicar 20 mg tablet
propecia 2017
zoloft online australia
synthroid 37 5 mg
where to purchase propecia
indocin medication
medrol 8mg tablet price
prozac india cost
buy zoloft online no prescription
generic benicar pills
generic wellbutrin canada
atarax hydrochloride
clonidine adhd adults
prescription atarax 25mg
plavix canada price
vermox drug
100mg prednisolone
order generic propecia online
where can i get seroquel
vermox online usa
celebrex tab 200mg
lisinopril 20 mg price without prescription
zestoretic 5 mg
buspar 30 mg cost
cafergot drug
xenical tablets price in india
where to buy atarax
zoloft 2019
seroquel 0.5 mg
clonidine hydrochloride 0.1 mg
buy atarax tablets
clopidogrel cost
how much is seroquel 100mg
priligy australia
benicar generic coupon
tenormin 105
atenolol online
zyban nz
indocin cream
clindamycin 75
can you buy elimite cream over the counter
online pharmacy australia
2.5 mg propecia
best no prescription pharmacy
price of celebrex in south africa
buying cytotec online
tizanidine cream price
propecia pills for sale
buy clindamycin cream uk
phenergan on line
cymbalta brand
buy tadacip from india
zithromax cost in mexico
benicar medication
plavix 75 mg pill buy clopidogrel 75 mg uk plavix.com
celebrex 800 mg can you buy generic celebrex celebrex tablet 200mg
Don’t settle for mediocre Lasix India – our premier products get the job done right.
budesonide capsule brand name budesonide 100 mcg budesonide online
These medicine allopurinol tablets are a lifesaver for people with chronic gout.
It’s important to use caution when driving or operating heavy machinery while taking Accutane 40mg as it can cause drowsiness.
colchicine 0.6 mg tablet generic colchicine tablets for sale colchicine 06 mg
tadacip 20 online
augmentin 875 125 mg cheap price
clomid price
antabuse 250 mg tablets
canadian neighbor pharmacy
trazodone generic cost
clindamycin hcl 300 mg buy
foreign pharmacy online
buy augmentin online usa
purchase zofran
erectafil 5 mg
clomid mexico pharmacy
endep without prescription
how much is zofran cost
amitriptyline online purchase
azithromycin buy online us
lyrica cheap online
atenolol
purchase cheap viagra online
provigil mexico prescription
diflucan drug
modafinil online pharmacy india
ivermectin pill cost
suhagra 25 mg price
tenormin drug
phenergan canada otc
buy stromectol pills
where can i buy metformin over the counter uk
generic for hydroxychloroquine 200 mg
elimite canada
buy zovirax usa
order lasix 100mg
can you buy ventolin over the counter uk
zovirax best price
cymbalta 30 mg coupon
plaquenil 200 mg 60 tab
zovirax 800 tablet
how much is acyclovir 800 mg
strattera coupon
flomax 0.4 mg daily
buy female cialis
cost of levaquin
erythromycin buy
piroxicam tablet
medrol generic prices
viagra cost usa
buy generic cialis no prescription
buy cheap avodart
cialis 10mg canadian pharmacy
piroxicam coupon
buy erectafil
purchase diflucan online
cost of propecia 1mg
can you buy atarax over the counter uk
buy online 10mg prednisolone
glucophage 1000 mg tablets
prednisolone 0.5 cream
cymbalta lowest price
baclofen over the counter australia
triamterene tablets
metformin er 1000
atarax cream price
lioresal price
over the counter atarax
order prednisolone
atenolol 25 mg price in india
prazosin medication generic
zestril brand
diclofenac 1.6 gel
cost of prednisone 10 mg tablet
50 mg accutane
clopidogrel
propecia tablets online india
propecia generic finasteride
doxycycline pharmacy
quineprox 400
buy doxycycline monohydrate
diflucan 400mg without prescription
cheap phenergan tablets
augmentin 400
buy septra ds 800/160 mg online without prescription
cheap online pharmacy
suhagra 500
diflucan tablet price in india
buy ventolin online nz
50 prednisolone
acyclovir prescription price
buy gabapentin canada
best price for cymbalta 60 mg
pill pharmacy
buy provigil online pharmacy
dexamethasone 0.5 tablet
buy azithromycin online pharmacy
terramycin eye ointment for cats
diflucan prices
clonidine 5 mg
can you buy cialis online from canada
tadalafil price uk
buying diflucan
voltaren gel 60 mg
buy azithromycin australia
metformin 2018
toradol pain shot
toradol price
metformin generic canadian pharmacy
lexapro generic 20 mg
can you diflucan over the counter
toradol pills 10 mg
furosemide australia
neurontin cost in singapore
legit non prescription pharmacies
wellbutrin price in india
valtrex cream coupon
prednisolone 5mg price uk
stromectol online
buy zoloft online usa
valtrex pills price
ivermectin tablets
generic ivermectin cream
bupropion er
finasteride tablet price
neurontin cap 300mg price
cheap propecia for sale
bupropion online uk
ivermectin lotion for scabies
cheap prednisolone
gabapentin from india
ivermectin 8000 mcg
zoloft where to buy
propecia .5 mg
buy propecia 1mg online
price of propecia
500mg amoxicillin capsules
wellbutrin 300 mg price
augmentin uk online
buy tetracycline online without a prescription from canada
biaxin price in india
myambutol price
keflex 250 mg
chloramphenicol sodium succinate
buy generic baclofen
sumycin otc
buy fincar online
6 baclofen
generic viagra without rx
best modafinil brand india
prescription motrin pills
tadacip 5mg
furosemide 80 tablet
augmentin 62.5 mg
elimite over the counter uk
xenical tablets price in south africa
cost of strattera without insurance
modafinil cost india
buy prednisolone 5mg tablets uk
amoxicillin pills
cheap fildena 100
order metformin online canada
can you buy furosemide over the counter tablets
top mail order pharmacies
advair 500 50 mg
ivermectin buy nz
antabuse pills online
buy clomid no prescription
plaquenil price in india
doxycycline 250
generic for lasix
where to buy fildena
flomax 0.4 mg over the counter
buy xenical singapore
average price of accutane
propecia generic canada
synthroid 50mcg
provigil price in india
levitra 10 mg canadian
buy prednisolone 5mg uk
proventil inhaler for sale
cheap cialis generic online
prednisolone pack
effexor uk
robaxin 750mg
dexamethasone brand name canada
nolvadex uk pharmacy
ventolin online canada
canadian pharmacy uk delivery
albuterol 90
generic furosemide 40 mg
azithromycin buy online us
where can i get acyclovir cream over the counter
trental drug
clonidine for sleep in adults
tretinoin gel otc
diflucan 1 pill
can i buy azithromycin over the counter in canada
tadacip 20 tablet
augmentin online nz
dipyridamole capsules 200mg
avodart best price
propranolol purchase
clonidine 5mg
suhagra 50 mg online
lasix tablets 20 mg
buy valtrex online canada
buy synthroid 150 mcg online
zovirax otc uk
azithromycin 250 mg tablets
zithromax buy canada
metformin price south africa
buy valtrex online without prescription
tenormin 25 mg tab
tretinoin gel price
how much is tetracycline cost
dipyridamole 25 mg tablet
buy fluconazol
60 lisinopril cost
prednisone canada pharmacy
synthroid generic brand
best propranolol brand
tretinoin gel for sale
paroxetine cheap
accutane medicine buy
accutane purchase
inderal 10 mg
where to buy ampicillin
where to buy diflucan in singapore
ventolin 4mg tab
doxycycline 40 mg price
price of prednisone
lyrica capsule
ventolin 4mg tablet
cheap metformin uk
buy diflucan 150 mg online
generic accutane for sale
baclofen generic price
rx lisinopril
generic diflucan otc
lyrica cost in india
zestril 20 mg tablet
dexamethasone 0.75 mg tablet
buy doxycycline
buy zithromax online paypal
cheapest pharmacy canada
buying metformin er
baclofen 20 mg price
buy valtrex tablets
where can i get prednisone over the counter
lisinopril 20 mg price in india
lisinopril 2.5 mg for sale
buy accutane uk
diflucan online paypal
fluconazole without script
albuterol purchase without prescription canada
who sells difluican with out a prescription
no prescription prenisone
doxycycline with out a rx
synthroid coupon
diflucan nz
where to buy prednisone online without a script
buy lisinopril 5mg
generic deltasone
lisinopril 200 mg
lisinopril 20 mg prescription
where to buy prednisone online without a script
doxycycline cheap australia
furosemide 500mg tablets
buy ventolin online usa
lyrica cheap online
azithromycin 250 mg buy online
zithromax otc
promo code for canadian pharmacy meds
valtrex medication for sale
generic accutane for sale
lyrica 150 mg price
suhagra 25 mg price
elimite cream for sale
synthroid 0.125
prednisone online no prescription
zestoretic 20 mg
synthroid tablets 100 mcg
where can you get prednisone
synthroid 112 mcg price
buy clomid online india
valtrex online pharmacy
synthroid 175 mcg tablet
lyrica prescription cost
wellbutrin generic price
amoxicillin uk price
buy cheap synthroid
generic cialis 20mg price
paroxetine 100 mg tablet
225 effexor
phenergan drug
pharmacy accutane
bactrim 168 mg
doxycycline 100mg dogs
synthroid 5 mcg
allopurinol generic price
toradol 30
buy propecia in canada
prozac 10
buy stromectol online uk
amoxicillin 875 mg cost
propranolol over the counter australia
doxycycline 100mg without a prescription
can you order accutane online
finasteride 1 mg coupon
buy retin a gel
lyrica 30 mg
effexor xr 37.5 mg
vardenafil 20 mg
where to buy amoxicillin 500mg
vermox pills
where can i buy tretinoin gel
desyrel 25 mg
lasix 1975
buy propranolol online usa
where to buy clomid
prescription amoxicillin
metformin for sale in usa
propecia canada online
cheap doxycycline online
online pharmacy 365 pills